Способы оценки влияния факторов в детерминированном факторном анализе

В общем виде детерминированную модель можно представить в виде функции нескольких переменных:

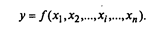
Задача детерминированного факторного анализа заключается в определении или количественной оценке влияния каждого фактора на результативный показатель.

Способы детерминированного факторного анализа перечислены в §2.2 (рис. 2.2). Наиболее часто применяется способ цепных подстановок, основанный, как и ряд других, на элиминировании. Элиминировать - это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходят из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все другие остаются без изменения, потом изменяются два при неизменности остальных и так далее.

Способ цепных подстановок. Этот способ заключается в определении ряда промежуточных значений результативного (обобщающего) показателя путем последовательной замены базисных значений факторов на отчетные. Разность промежуточных значений равна изменению результативного показателя за счет заменяемого фактора. В формализованном виде алгоритм применения способа цепных подстановок описывается следующим образом:

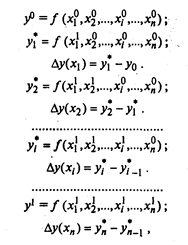
где «нулевые» значения (индекс ⁰) — базисные; «единичные» значения (индекс ¹) - отчетные или фактические; у_i* — промежуточное значение результата.

Общее изменение результата Δу = у¹ - у⁰ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных остальных факторах, т.е. Δу = 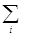Δу(х_i).

Число расчетов результативного показателя на единицу больше числа измеряемых факторов. Преимущества данного способа: универсальность применения (применяется в анализе любых типов моделей), достаточная простота применения.

Однако этот метод имеет существенный недостаток - в зависимости от выбранного порядка замены факторов результаты факторного разложения имеют разные значения.

В результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. Но в практических расчетах точностью оценки влияния факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Тем не менее существуют некоторые правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь, производится подстановка количественных факторов;

• если модель представлена несколькими количественными или качественными показателями, последовательность подстановки определяется путем логического анализа. Зависимость объема выпуска продукции от среднегодовой численности персонала и выработки описывается двухфакторной моделью:

Рассмотрим пример.

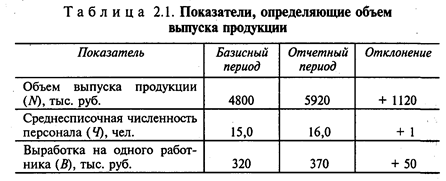
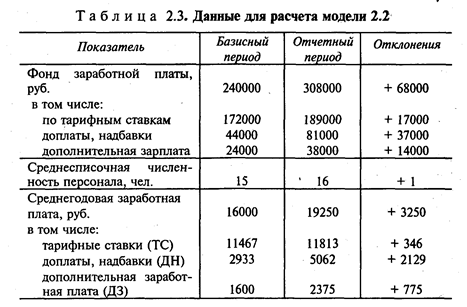
Алгебраическая сумма влияния факторов должна быть равна приросту результативного показателя. Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах. Результаты расчетов оформляются таблицей (в данном примере табл. 2.2). Это особенно важно, если модель многофакторная, а также в том случае, если изучается влияние факторов второго, третьего и т.д. порядков.

Количество расчетов может быть несколько сокращено, если использовать модификацию способа цепной подстановки — способ разниц.

Способ абсолютных разниц. Алгоритм решения двухфакторной мультипликативной модели методом цепной подстановки описывается следующим образом:

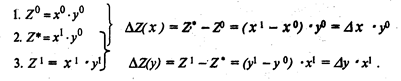
Таким образом, изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого (других) факторов в зависимости от выбранной последовательности подстановки.

Изменение последовательности подстановки выявляет разницу в расчетах, называемую неразложимым остатком, который в данном случае составит 50 тыс. руб.

Для распределения между факторами неразложимого остатка, который при способе цепной подстановки прибавляется к размеру влияния качественного фактора, используют следующие приемы: простое прибавление неразложимого остатка и прием взвешенных конечных разностей.

Прием простого прибавления неразложимого остатка предполагает деление неразложимого остатка на 2 и прибавление результата к величине влияния качественного и количественного факторов.

Формулы определения влияния факторов принимают вид:

Остаточный член в линейном разложении функции Z = х ∙ у равен Δх ∙ Δу. Докажем это.

Если считать, что ΔZ(x) = Δx ∙ y⁰иΔZ(y) = Δу ∙ х⁰, тогда остаточный член (неразложимый остаток) равен разности между отклонением результативного показателя от суммы влияния факторов х и у, т.е. неразложимый остаток равен ΔZ — [(ΔZ (х) + ΔZ (у)]. Преобразуем это выражение:

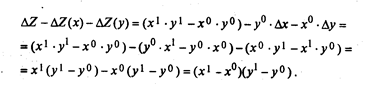
В рассматриваемом примере:

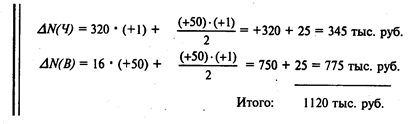
Но данный способ расчета неприменим при количестве факторов больше двух. В случае большего количества факторов в факторной модели применяется прием взвешенных конечных разностей. Суть его: величина влияния каждого фактора определяется по всем возможным подстановкам, затем результат суммируется и от полученной суммы берется средняя величина. Математически это записывается:

Продолжение примера:

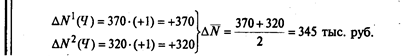
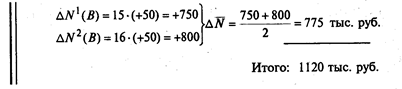
Рассмотренный способ применим для детерминированных моделей с любым количеством факторов, но он весьма трудоемок, и затраты на его реализацию несопоставимы с выгодами, получаемыми в результате применения.

Пропорциональное распределение остатка по факторам достигается с помощью логарифмического метода.

Логарифмический способ. Достоинство этого способа в том, что он позволяет определить влияние не только двух, но и большего количества факторов на результативный показатель без установления очередности подстановок.

Способ применим к кратным и мультипликативным моделям. Он основан на логарифмировании отклонения отчетного и базисного значений результативного признака, равного отношению соответствующих произведений факторов, так как изменение показателей может быть оценено с помощью как абсолютных, так и относительных показателей.

Мультипликативная факторная модель Z = x ∙ y ∙ a ∙ b может быть представлена так:

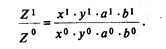
Логарифмируя выражение, получим

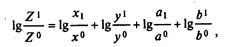
или

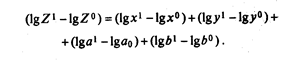
Умножим каждую часть равенства на коэффициент

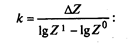
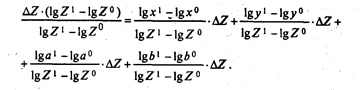
Если обозначить отношения при ΔZ через коэффициенты k_х, k_y, k_а и k_b,, то выражение примет вид:

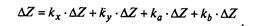
Таким образом при помощи коэффициентов k производится пропорциональное распределение совокупного отклонения между факторами. Математическое содержание коэффициентов идентично «способу долевого участия».

Способ долевого участия. Этот способ заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост совокупного показателя. Этот метод применяется к аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков.

Для примера рассмотрим модель зависимости фонда заработной платы от средней заработной платы и численности персонала

где ФЗ - фонд заработной платы; ЗП — средняя заработная плата; Ч — среднесписочная численность.

В свою очередь средняя заработная плата равна сумме средних выплат по тарифным ставкам, доплат, надбавок (ДН) и дополнительной заработной платы (ДЗ).

Модель примет вид:

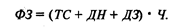
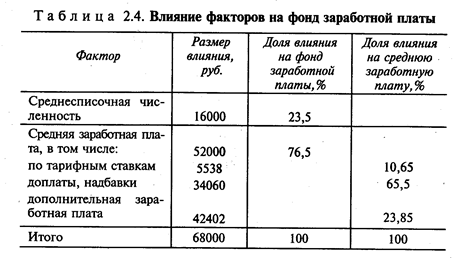
Индексный метод. Основан на построении факторных (агрегированных) индексов. Применение агрегированных индексов означает последовательное элиминирование влияния отдельных факторов на совокупный показатель. Преимущество индексного метода заключается в том, что он позволяет произвести «разложение» по факторам не только абсолютное изменение показателя, но и относительное, что особенно важно при изучении факторных динамических моделей.

Так, индекс изменения выпуска продукции можно выразить через произведение индексов численности и выработки.

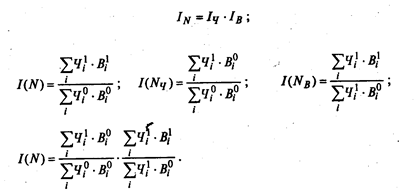
С помощью индексного метода можно определить влияние факторов, в том числе структурных сдвигов, на абсолютное отклонение результативного показателя:

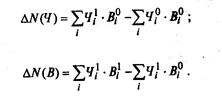
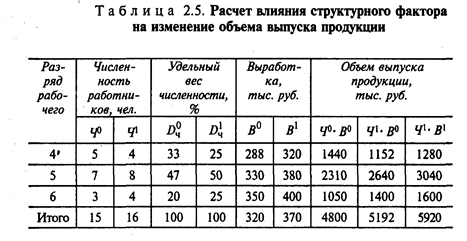
Индексный метод целесообразно применять в том случае, когда каждый фактор является сложным (совокупным) показателем. Например, численность персонала предприятия представляет собой соотношение численности отдельных категорий работников или рабочих различных разрядов. Но изменение объема выпуска продукции происходит не только под влиянием численности и выработки, но и структурных сдвигов в составе персонала. Рассчитанное методом цепной подстановки влияние изменения выработки на изменение объема выпуска продукции (в примере с данными табл. 2.1), составившее 800 тыс. руб., происходит под влиянием изменения выработки рабочих различных разрядов и структурных сдвигов в составе персонала.

Все рассмотренные способы — способ цепной подстановки, способ разниц, приемы простого прибавления неразложимого остатка и взвешенных конечных разностей, способ долевого участия и логарифмический основаны на элиминировании, т.е. изучении влияния каждого фактора независимо от других. Однако в действительности изменение одного фактора порождает изменение всех других. В связи с этим результаты расчетов являются в определенной степени условными и отражают тенденции, сложившиеся в хозяйственном процессе.

Интегральный способ. Этот способ позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, так как в нем действует логарифмический закон перераспределения факторных нагрузок.

Интегральный метод позволяет достигнуть полного разложения отклонения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям.

Операция вычисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется по стандартной программе с помощью ЭВМ. Задача сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.

При отсутствии универсальных вычислительных средств можно применять формулы расчета влияния факторов, являющиеся результатом выполнения процессов интегрирования, а также использовать уже сформированные рабочие формулы для расчетов — см., например, [6, с. 135—143].

Формулы расчета влияния факторов в мультипликативных моделях:

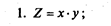
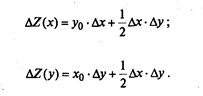
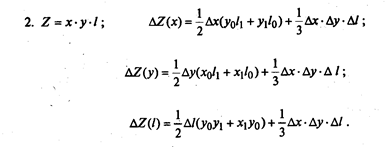
Формулы расчета влияния факторов в кратных и смешанных моделях:

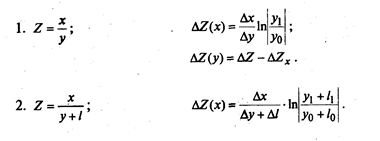
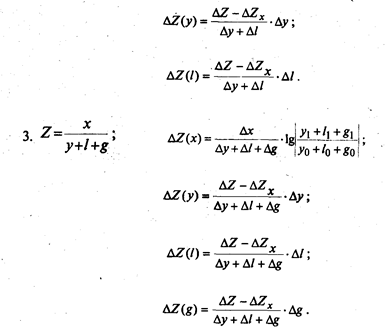
Важной особенностью метода является то, что он дает общий подход к решению задач самого разного вида независимо от количества элементов, входящих в модель факторной системы, и формы связи между ними.