Матричный метод и его применение в сравнительном многомерном анализе

Матричные методы анализа основаны на линейной и векторно-матричной алгебре и применяются для изучения сложных и многомерных структур. Сферы применения матричного метода как метода экономического анализа многообразны, но наиболее широкое распространение получил метод для сравнительной оценки деятельности различных систем (предприятий, структурных подразделений и т.п.).

В результате сравнительного анализа определяется рейтинг анализируемых систем. Рассмотрим алгоритм применения матричного метода.

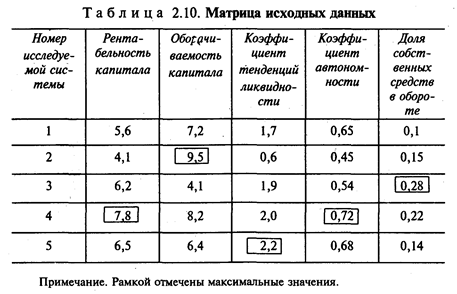
Этап 1. Обоснование системы оценочных показателей и формирование матрицы исходных данных a_ij, т.е. таблицы, где по строкам отражаются номера систем (i = 1, 2, ..., п), а по столбцам - номера показателей (j = 1, 2, ..., т).

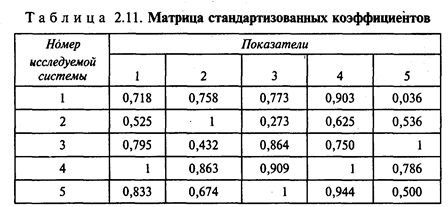
Этап 2. В каждой графе определяется максимальный элемент, который принимается за единицу. Затем все элементы этой графы a_ij делятся на максимальный элемент эталонной системы mахa_ij и создается матрица стандартизованных коэффициентов x_ij.

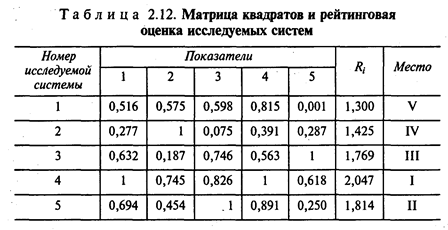
Этап 3. Все элементы матрицы возводятся в квадрат. Если значимость показателей, составляющих матрицу, различна, тогда каждому показателю присваивается весовой коэффициент k, который определяется экспертным путем.

Рейтинговая оценка по каждой системе определяется по формуле:

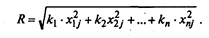
Этап 4. Полученные рейтинговые оценки R_j размещаются в порядке убывания или возрастания, что зависит от экономического смысла показателей, составляющих рейтинг.

Результаты описанного сравнительного анализа могут применяться для определения инвестиционной привлекательности партнера, эмитента и для других целей.

Этап 1

Этап 2.

Резюме

Метод экономического анализа как совокупность приемов и способов применим для изучения поведения объекта исследования на различных стадиях жизненного цикла системы и для решения любых управленческих задач. Множество технических приемов и способов группируется по ряду признаков: научному подходу, характеру взаимосвязи, степени сложности применяемого инструментария, методам оптимизации.

Одной из основных задач и особенностей анализа является количественная оценка взаимосвязи показателей, описывающих состояние системы. На выявление и измерение взаимосвязи показателей направлены методы детерминированного и стохастического факторного анализа. Методы детерминированного факторного анализа требуют построения факторных моделей, которые можно свести к четырем типам: аддитивные, мультипликативные, кратные, смешанные.

Наиболее распространенными способами факторного детерминированного анализа являются метод цепной подстановки и его модификации — способ абсолютных разниц; способ простого прибавления неразложимого остатка, способ взвешенных конечных разностей; логарифмический способ долевого участия, интегральный, индексный. Выбор способа изучения факторной модели определяется его преимуществами перед остальными в каждой конкретной ситуации и в применении к конкретным аналитическим задачам. Характеристики способов детерминированного факторного анализа сведены в табл. 2.13.

Для изучения стохастических, вероятностных взаимосвязей применяется корреляционно-регрессионный метод анализа. Его применение позволяет количественно оценить тесноту связи между изучаемыми величинами, дать оценку доли влияния факторов на результативный показатель, описать форму взаимосвязи, определить прогнозное значение совокупного показателя при изменении факторного.

Вопросы для контроля

1. Какие отличительные особенности характеризуют метод экономического анализа?

2. Какие принципы лежат в основе классификации приемов и способов анализа?

3. Чем отличаются способы детерминированного и стохастического факторного анализа?

4. Какую роль в экономическом анализе выполняет способ сравнения?

5. Объясните способы построения детерминированных факторных моделей.

6. Опишите алгоритм применения наиболее простых способов детерминированного факторного анализа: способа цепных подстановок, способа разниц. Какие приемы применяются для распределения неразложимого остатка по факторам?

7. Охарактеризуйте достоинства и опишите алгоритм применения логарифмического и интегрального методов.

8. Приведите примеры задач и факторных моделей, к которым применяется каждый из методов детерминированного факторного анализа.

9. В какой последовательности применяется корреляционно-регрессионный метод изучения линейной и нелинейной форм связи?

10. Опишите значение и алгоритм применения матричного метода.