СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ

;

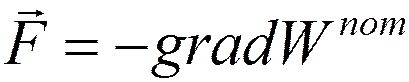разделив на величину заряда q_0, получим

.

;

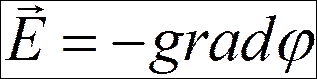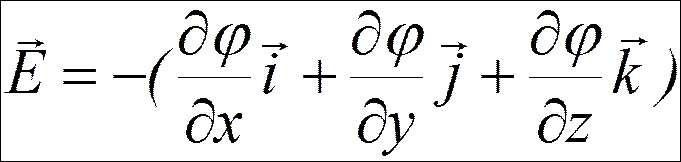Проекции вектора напряженности

;

;

;

:

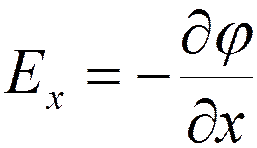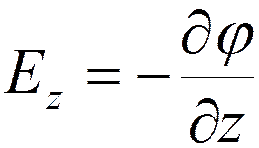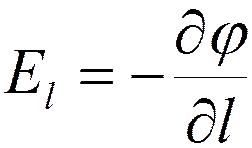
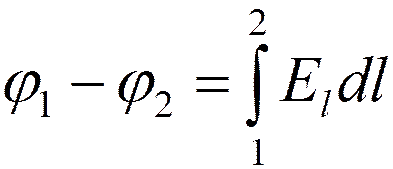Или

.

В однородном поле ;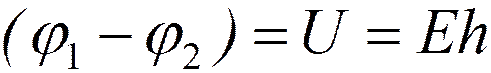

здесь h = l₁₂

1 СИj =1 В

1 В = 1 СИ_Е ^.1 м Þ 1 СИ E = 1 В /м

Любой заряд q, находящийся в эл. поле в точке, потенциал которой j, обладает потенциальной энергией

.

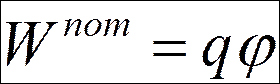Работа сил электростатического поля по перемещению заряда q из данной точки в бесконечность

.

Потенциальная энергия взаимодействия точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга:

.

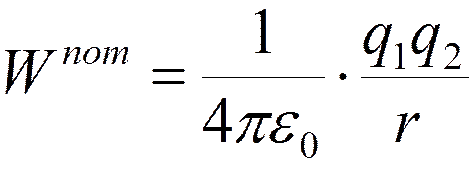Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2

.

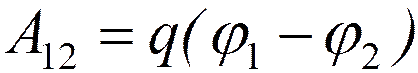Пусть (^.)1 ® (^.)2, тогда (j1- j2) ® 0,

А₁₂ ® 0

-

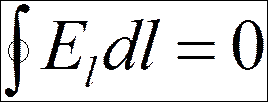- теорема о циркуляции напряженности электростатического поля или условие потенциальности электростатических полей.

Если поле создано системой зарядов, потенциал его определяется алгебраической суммой потенциалов полей, созданных каждым зарядом в отдельности (принцип суперпозоции):

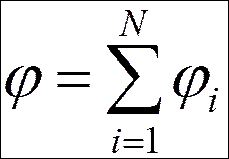
При графическом изображении полей кроме силовых линий изображают эквипотенциальные поверхности, т.е. поверхности равного потенциала

Уравнение эквипотенциальной поверхности j (x,e,z) = 0