и допустимые базисные решения ЗЛП
Пусть 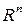 –n–мерное векторное пространство над полем R и V – некоторое его подмножество. Определим выпуклость множества V как и в случае n = 2:
–n–мерное векторное пространство над полем R и V – некоторое его подмножество. Определим выпуклость множества V как и в случае n = 2:
Множество V называется выпуклым, если с любыми двумя своими точками 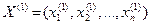 и
и 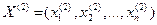 оно содержит отрезок
оно содержит отрезок 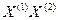 , т.е. все точки
, т.е. все точки 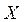 вида (1):
вида (1):
(1) 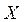 =
= 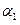
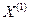 +
+ 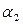
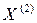 ,
, 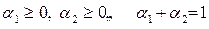 ,
,
Среди точек выпуклого множества можно выделить точки внутренние, граничные и угловые (вершины).
Точка множества называется внутренней, если существует ее окрестность, в которой содержатся только точки данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Граничная точка выпуклого множества называется угловой (вершиной), если она не является внутренней ни для одного отрезка, целиком принадлежащего данному множеству.
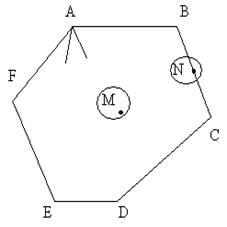
Рис. 4. 1
На рис. 1 изображены внутренняя точка M, граничная точка N, угловые точки A, В, C, D, E, F выпуклого многоугольника ABCDEF.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует n–мерный шар конечного радиуса, который содержит в себе данное множество; в противном случае оно называется неограниченным. Примерами замкнутого ограниченного выпуклого множества точек являются любой выпуклый многоугольник на плоскости или выпуклый многогранник в пространстве.
Выпуклое замкнутое множество точек n–мерного пространства, имеющее конечное множество угловых точек, называется выпуклым n–мерным многогранником, если оно ограниченное, и выпуклой n–мерной многогранной областью, если оно не ограничено.
Рассмотрим задачу линейного программирования в стандартной форме с n переменными (n ³2).
Дана система линейных неравенств вида (2):
(2) 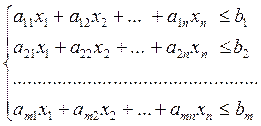 в которой m < n,
в которой m < n,
и целевая линейная функция (3) f = 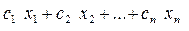 . Требуется найти допустимое (т.е. неотрицательное) решение системы (2), при котором функция f принимает наименьшее (или наибольшее) значение.
. Требуется найти допустимое (т.е. неотрицательное) решение системы (2), при котором функция f принимает наименьшее (или наибольшее) значение.
Теорема 1. Множество допустимых решений системы (2) m линейных неравенств с n переменными является выпуклым n–мерным многогранником (выпуклой n–мерной многогранной областью).
Ответ на вопрос, в какой точке многогранника допустимых решений целевая функция достигает оптимального значения, указывается в следующей теореме.
Теорема 2. Если задача (2), (3) имеет оптимальное решение, то целевая функция принимает минимальное (максимальное) значение в одной из угловых точек многогранника допустимых решений.
Таким образом, вместо исследования бесконечного множества допустимых решений системы (2) для нахождения среди них оптимального решения, достаточно исследовать лишь конечное число угловых точек многогранника допустимых решений. Доказательство теорем 1 и 2 можно найти в [15].
Следующая теорема определяет алгебраический метод нахождения угловых точек многогранника допустимых решений.
Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника допустимых решений, и наоборот, каждой угловой точке многогранника допустимых решений соответствует допустимое базисное решение задачи.
Рассмотрим систему ограничений ЗЛП в канонической форме: дана система линейных уравнений вида (4):
(4) 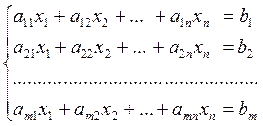
у которой ранг матрицы A системы r = m < n. Покажем, что каждое допустимоебазисное решение системы является угловой точкой многогранника M допустимых решений задачи.
Пусть 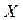 =
= 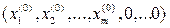 – допустимое базисное системы (4). Для простоты считаем, что первые m значений переменных решения
– допустимое базисное системы (4). Для простоты считаем, что первые m значений переменных решения 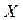 соответствуют линейно независимым столбцам коэффициентов матрицы A . Обозначим эти столбцы коэффициентов символами
соответствуют линейно независимым столбцам коэффициентов матрицы A . Обозначим эти столбцы коэффициентов символами 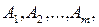 а столбец свободных членов системы (4) – символом B. Покажем, что
а столбец свободных членов системы (4) – символом B. Покажем, что 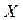 – угловая точка многогранника допустимых решений задачи.
– угловая точка многогранника допустимых решений задачи.
Предположим противное, т.е. что точка 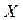 не является угловой точкой многогранника M . Тогда ее можно представить в виде выпуклой комбинации (1) двух различных точек многогранника M:
не является угловой точкой многогранника M . Тогда ее можно представить в виде выпуклой комбинации (1) двух различных точек многогранника M:
(5) 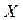 =
= 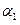
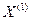 +
+ 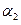
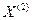 ,
, 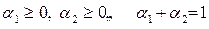 .
.
Точки 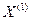 =
= 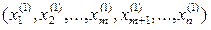 и
и 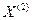 =
= 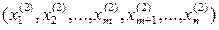 – допустимые решения системы (4). В координатной форме равенство (5) означает, что выполняется система равенств (6):
– допустимые решения системы (4). В координатной форме равенство (5) означает, что выполняется система равенств (6):
(6) 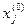 =
= 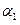
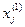 +
+ 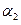
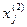 ,
, 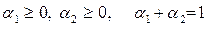 , j = 1,…,n.
, j = 1,…,n.
Так как последние (n – m) координат точки 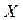 равны нулю, а числа
равны нулю, а числа 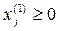 ,
, 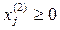 ,
, 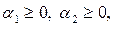 то последние (n – m) координат точек
то последние (n – m) координат точек 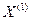 и
и 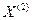 также равны нулю. Поэтому выполняются равенства:
также равны нулю. Поэтому выполняются равенства:
(7) 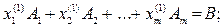
(8) 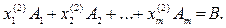
Вычитая почленно (8) из (7), получим:
(9) 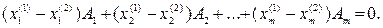
Точки 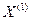 и
и 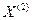 различны, следовательно, среди коэффициентов при
различны, следовательно, среди коэффициентов при 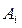 (I = 1,…, m) в (9) есть отличные от нуля. Это означает, что система векторов – столбцов
(I = 1,…, m) в (9) есть отличные от нуля. Это означает, что система векторов – столбцов 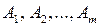 линейно зависима, что противоречит тому, что
линейно зависима, что противоречит тому, что 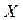 – допустимое базисное решение системы (4). Следовательно, наше предположение о том, что
– допустимое базисное решение системы (4). Следовательно, наше предположение о том, что 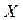 – не угловая точка, неверно, и
– не угловая точка, неверно, и 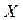 является вершиной многогранника допустимых решений системы.
является вершиной многогранника допустимых решений системы.
Докажем обратное утверждение. Пусть 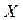 – угловая точка многогранника M. Если
– угловая точка многогранника M. Если 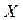 =
= 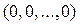 , то решение
, то решение 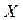 является, по определению 1, допустимым базисным решением. Пусть
является, по определению 1, допустимым базисным решением. Пусть 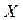
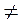
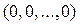 и для определенности
и для определенности 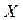 =
= 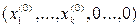 , т.е. первые k (k £ n) координат положительны. Предположим снова противное, т.е., что
, т.е. первые k (k £ n) координат положительны. Предположим снова противное, т.е., что 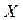 – допустимое но не базисное решение системы (4). Тогда столбцы коэффициентов
– допустимое но не базисное решение системы (4). Тогда столбцы коэффициентов 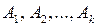 матрицы системы линейно зависимы, т.е. существуют такие действительные числа
матрицы системы линейно зависимы, т.е. существуют такие действительные числа 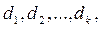 не все равные нулю, что выполняется равенство:
не все равные нулю, что выполняется равенство:
(10) 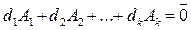 .
.
По условию точка 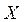 является решением системы (4):
является решением системы (4):
(11) 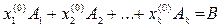 .
.
Умножим обе части равенства (10) на некоторый параметр 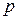
 и сначала вычтем полученное равенство почленно из (11), а затем сложим с (11):
и сначала вычтем полученное равенство почленно из (11), а затем сложим с (11):
(12) 
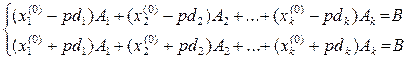
Так как 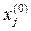 ³ 0 ( j =1, 2, …, k), то можно найти такое достаточно малое значение параметра
³ 0 ( j =1, 2, …, k), то можно найти такое достаточно малое значение параметра 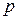 >0, что в системе (12) все коэффициенты будут неотрицательными. Тогда система (12) означает что точки
>0, что в системе (12) все коэффициенты будут неотрицательными. Тогда система (12) означает что точки
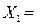
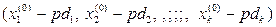 и
и
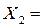
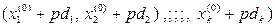
являются допустимыми различными решениями системы (4), и решение 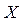 является их полусуммой:
является их полусуммой:
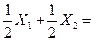
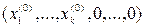 =
= 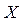 , а это противоречит тому, что
, а это противоречит тому, что 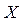 – угловая точка многогранника допустимых решений системы (4). Следовательно,
– угловая точка многогранника допустимых решений системы (4). Следовательно, 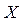 является допустимым базисным решением системы (4). Теорема доказана полностью.
является допустимым базисным решением системы (4). Теорема доказана полностью.
Заметим, что при вычислении допустимых базисных решений задачи нужно заменить неравенства системы (2) соответствующими уравнениями.
Из теорем 2 и 3 вытекает важное следствие: если задача линейного программирования имеет оптимальное решение, то одним из оптимальных решений является допустимое базисное решение. Если матрица системы уравнений (4) имеет ранг r = m < n, то число допустимых базисных решений не превышает 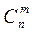 , и решение задачи сводится к конечному перебору допустимых базисных решений задачи.
, и решение задачи сводится к конечному перебору допустимых базисных решений задачи.
Пример. Дана система линейных неравенств:
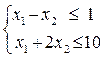
Найти неотрицательное решение системы, при котором функция
f = 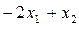 принимает наименьшее значение.
принимает наименьшее значение.
Решение. Перейдем к системе уравнений, заменяя неравенства соответствующими уравнениями:
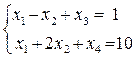
Система уравнений имеет ранг r = m =2, n = 4. 
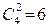 , т.е.базисных решений не больше 6. Пропорциональных столбцов коэффициентов нет, поэтому базисных решений будет 6.
, т.е.базисных решений не больше 6. Пропорциональных столбцов коэффициентов нет, поэтому базисных решений будет 6.
1. Базисному набору 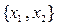 соответствуют свободные переменные
соответствуют свободные переменные 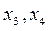 . Полагаем
. Полагаем 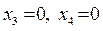 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 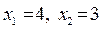 . Получили допустимое базисное решение
. Получили допустимое базисное решение 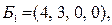 f(
f( 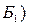 = -5.
= -5.
2. Базисному набору 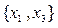 соответствуют свободные переменные
соответствуют свободные переменные 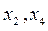 . Полагаем
. Полагаем 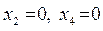 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 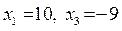 . Получили недопустимое базисное решение
. Получили недопустимое базисное решение 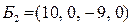 .
.
3. Базисному набору 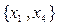 соответствуют свободные переменные
соответствуют свободные переменные 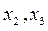 . Полагаем
. Полагаем 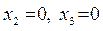 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 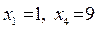 . Получили допустимое базисное решение
. Получили допустимое базисное решение 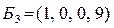 , f(
, f( 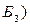 = –2.
= –2.
4. Базисному набору 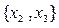 соответствуют свободные переменные
соответствуют свободные переменные 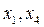 . Полагаем
. Полагаем 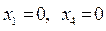 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 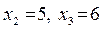 . Получили допустимое базисное решение
. Получили допустимое базисное решение 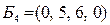 , f(
, f( 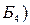 = 5.
= 5.
5. Базисному набору 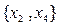 соответствуют свободные переменные
соответствуют свободные переменные 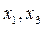 . Полагаем
. Полагаем 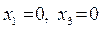 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 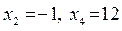 . Получили недопустимое базисное решение
. Получили недопустимое базисное решение 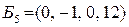 .
.
6. Базисному набору 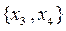 соответствуют свободные переменные
соответствуют свободные переменные 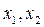 . Полагаем
. Полагаем 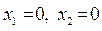 , из системы находим значения базисных переменных:
, из системы находим значения базисных переменных: 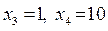 . Получили допустимое базисное решение
. Получили допустимое базисное решение 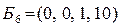 , f
, f 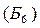 = 0.
= 0.
Оптимальным решением задачи является решение 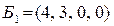 , при котором f(
, при котором f( 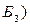 = –5 = min f.
= –5 = min f.
Четырехмерный многогранник допустимых решений задачи мы построить не можем, но по теореме 3 можно определить 4 его угловых точки: 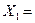
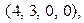
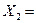
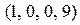 ,
, 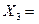
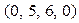 и
и 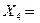
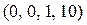 .
.
Дата добавления: 2016-04-14; просмотров: 2016;
