Различные случаи решения ЗЛП с двумя переменными

При геометрическом решении ЗЛП возможны следующие случаи:

1. Опорная прямая 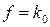соприкасается с областью М в единственной точке. Тогда ЗЛП имеет единственное оптимальное решение 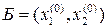и min .

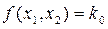2. Опорная прямая 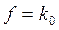имеет с областью М общий отрезок прямой. Тогда ЗЛП имеет бесконечное множество решений и min .

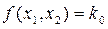3. Область М – неограниченная сверху (справа), и при уменьшении линия уровня движется вверх (вправо). Следовательно, уровень функции 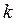может уменьшаться сколько угодно и min 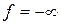. Это означает, что ЗЛП не имеет оптимального решения. Задача не будет иметь решения и в случае .

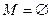Пример 1. Дать геометрическое истолкование и решить упражнение 2 к §1.

Решение. Область ограничений в упражнении может быть задана в стандартной форме:

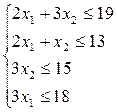
Среди неотрицательных решений этой системы неравенств нужно найти такое, которое минимизирует функцию .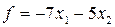

Выбрав систему координат 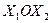, построим область ограничений (Рис. 3.7). Возьмем линию уровня , тогда 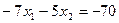. Вектор 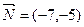показывает, что при увеличении 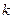линия уровня 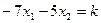движется влево и вниз, и первое прикосновение, как видно из рис.3. 7,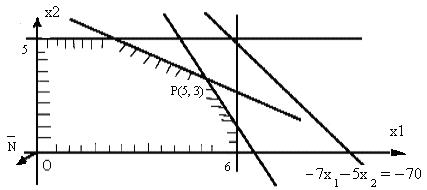

Рис. 3. 7

с областью М произойдет в точке пересечения прямых 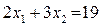и 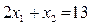. Это точка 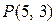. Значит оптимальным решением является решение 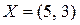и min .

В исходной задаче требовалось найти max 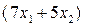. Как было отмечено ранее, оптимальное решение будет таким же, поэтому max = .

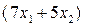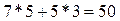2. Рассмотрим ЗЛП с той же системой ограничений:

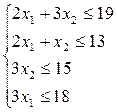
но с другой целевой функцией 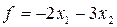. Требуется найти допустимое решение системы неравенств, которое минимизирует эту функцию.

Линии уровня функции 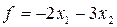параллельны прямой 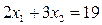. Поэтому опорная прямая 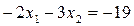пройдет по границе области ограничений М (по отрезку прямой 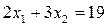), т.е. оптимальных решений у этой задачи бесконечное множество. Одно из них 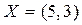, и min .

Пример 3. Найти неотрицательное решение системы неравенств:

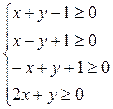
и минимизирующее линейную функцию .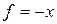

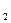Область допустимых решений ограничена тремя прямыми L , L и L 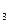, определяющими полуплоскости решений первых трех неравенств и является неограниченной сверху и справа. Линия уровня 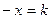при уменьшении k будет перемещаться вправо, а, значит, min 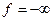и данная задача оптимального решения не имеет.

Рис. 3. 8

Мы видим, что геометрическое истолкование ЗЛП приводит к ее решению. Из рассмотренных примеров видно, что если ЗЛП имеет оптимальное решение при n=2, то одним из ее оптимальных решений являются координаты вершины (угловой точки) многоугольника допустимых решений системы ограничений задачи, в которой целевая функция имеет экстремум.

Таким же образом можно решить ЗЛП в канонической форме, в которой число переменных n больше количества уравнений m на 2. Тогда можно выбрать две переменные, остальные переменные и целевую функцию выразить из уравнений (как в примере с задачей 1 из §1) через них, затем решить графически ЗЛП с двумя переменными.

Аналогично можно истолковывать решение ЗЛП при большем числе переменных. При количестве переменных n=3 множество допустимых решений системы ограничений задачи геометрически представляет многогранную неограниченную выпуклую область или выпуклый многогранник, и одним из оптимальных решений задачи, если они существуют, будут координаты вершины (угловой точки) этого выпуклого многогранника (или многогранной области), в которой достигается экстремум целевой функции. При n>3 может быть сохранена геометрическая терминология, но решать ЗЛП графически уже невозможно.

§ 4. Системы линейных уравнений и выпуклые множества

1. Базисные решения системы линейных уравнений

Рассмотрим систему m линейных уравнений, содержащую n переменных

(1)

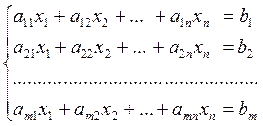
Эту систему можно записать короче в виде: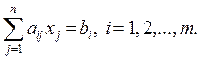

Или в матричной форме: Ax = B.

В задачах линейного программирования рассматриваются неопределенные системы уравнений, т.е. имеющие бесконечное множество решений. Тогда ранг r матрицы системы 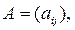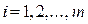, 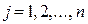меньше числа переменных: r<n. Это означает, что максимальное число линейно независимых уравнений в (1) равно r. Будем считать, что в системе (1) число линейно независимых уравнений равно m, т.е. r = m. Из алгебры известно, что в этом случае найдутся m переменных, коэффициенты у которых в системе (1) образуют матрицу с определителем, отличным от нуля. Такой определитель называется базисным минором, а соответствующие переменные – базисными. Остальные n – m переменных называются свободными переменными. Базисные переменные можно выразить через свободные переменные с помощью уравнений системы (1), присвоить свободным переменным произвольные значения и найти значения базисных переменных по формулам Крамера. Получится одно из решений системы (1).

Определение 1. Решение системы линейных уравнений (1), полученное при нулевых значениях свободных переменных, называется базисным решением.

Базисные переменные, а поэтому и ненулевые компоненты базисного решения соответствуют линейно независимым столбцам матрицы коэффициентов системы линейных уравнений. Это позволяет дать другое определение базисного решения системы линейных уравнений.

Определение 2.Базисным решением системы линейных уравнений называется решение этой системы, ненулевые компоненты которого соответствуют линейно независимым столбцам матрицы коэффициентов этой системы.

В качестве базисных переменных могут быть разные группы, содержащие m переменных из заданных в (1) n переменных. Максимальное возможное число способов выбора m переменных из множества, содержащего n переменных, равно числу сочетаний 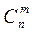. Однако могут встретиться случаи, когда соответствующий определитель матрицы, составленной из коэффициентов при выбранных m переменных в системе (1), равен нулю. Поэтому число групп базисных переменных не превосходит 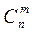. Для каждой группы базисных переменных можно найти соответствующее базисное решение системы (1). Из приведенных выше рассуждений вытекает теорема:

Теорема. Число базисных решений неопределенной системы (1), в которой ранг матрицы системы r = m < n не превосходит .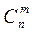

Пример. Найти все базисные решения системы уравнений (2):

(2)

Решение. Очевидно r=m=2, n=4. Общее число групп базисных переменных не более чем 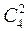= 6. Однако первый, второй и четвертый столбцы коэффициентов у переменных в матрице системы – пропорциональные, поэтому определители второго порядка, составленные из коэффициентов любых двух из этих трех столбцов, равны нулю. Остаются наборы: 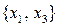, 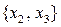и .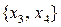

Для набора переменных 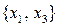определитель, составленный из их коэффициентов d = = –2 ¹ 0. Следовательно, эти переменные можно считать базисными переменными, 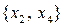– свободными. Присвоим свободным переменным нулевые значения: 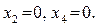Решаем систему:

(3) 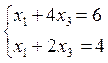, откуда .

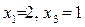Получили первое базисное решение: Б = (2, 0, 1, 0).

Аналогично докажем, что наборы переменных 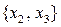и 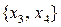являются базисными наборами. Присваивая соответствующим свободным переменным нулевые значения, найдем еще два базисных решения системы (1): Б 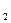= (0, –1, 1, 0) и Б 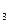= (0, 0, 1, ).

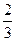В задачах линейного программирования особый интерес представляют допустимые (т.е. неотрицательные) базисные решения. В рассмотренном примере из трех базисных решений только два ( первое и третье) являются допустимыми базисными решениями. Очевидно, число допустимых базисных решений системы (1) не превосходит .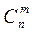

Базисное решение, в котором хотя бы одна базисная переменная равна нулю, называется вырожденным. В рассмотренном примере вырожденных базисных решений нет.

2. Выпуклые множества в n – мерном пространстве