Полярное уравнение эллипса, гиперболы и параболы.
Часто используют уравнения эллипса, гиперболы и параболы в полярной системе координат. Мы фиксируем полюс полярной системы координат в фокусе кривой. При этом для эллипса выбираем левый фокус, а для гиперболы - правый. Полярную ось выбираем так, чтобы её направление совпадало с положительным направлением оси абсцисс.
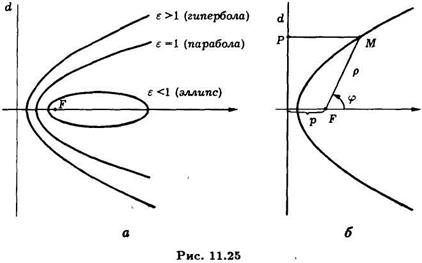
Все три вида кривых описываются общим свойством: для любой точки отношение расстояний до фокуса и до директрисы постоянно и равно эксцентриситету кривой. Значение эксцентриситета определяет тип кривой. Если зафиксировать фокальный параметр (это расстояние от фокуса до директрисы) так, что положение директрисы в выбранной системе координат будет оставаться неизменным, то варьируя эксцентриситет, получим единый ряд эллипсов, параболы, правых ветвей гипербол (См. рис. 11.25). Конкретная кривая определяется своим эксцентриситетом 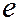 при помощи уравнения:
при помощи уравнения: 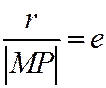 , (4)
, (4)
где 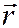 - полярный, он же фокальный радиус точки
- полярный, он же фокальный радиус точки 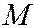 на кривой,
на кривой, 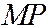 - перпендикуляр, опущенный из точки
- перпендикуляр, опущенный из точки 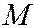 на директрису
на директрису 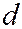 (См. рис. 11.25 ).
(См. рис. 11.25 ).
|
Так как 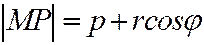 , то подставив это выражение в (4), получим:
, то подставив это выражение в (4), получим: 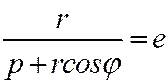 или
или 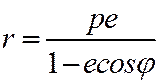 (5)
(5)
Уравнение (5) называется полярным уравнением эллипса, параболы, правой ветви гиперболы.
Дата добавления: 2016-04-14; просмотров: 1133;
