Исследование формы параболы.
Так как ордината 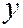 в каноническое уравнение параболы входит во второй степени, то ось
в каноническое уравнение параболы входит во второй степени, то ось 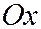 является осью симметрии параболы
является осью симметрии параболы 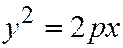 .
.
Определение. Точка пересечения параболы с её осью симметрии называется вершиной параболы. Парабола (1) имеет только одну вершину 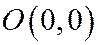 .
.
Из уравнения 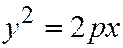 следует, что
следует, что 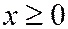 (т.к.
(т.к. 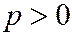 , а
, а 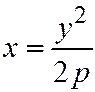 ). Разрешая уравнение
). Разрешая уравнение 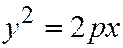 относительно
относительно 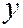 и беря для
и беря для 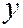 лишь неотрицательное значение
лишь неотрицательное значение 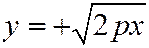 , видим, что в полуинтервале
, видим, что в полуинтервале 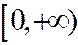
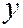 - возрастающая функция
- возрастающая функция 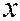 , причём
, причём 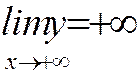 .
.
Всякая прямая пересекает параболу не более чем в двух точках (т.к. прямая определяется уравнением первой степени, а парабола - второй. Проведённое исследование даёт представление о форме параболы (См. рис. 177).
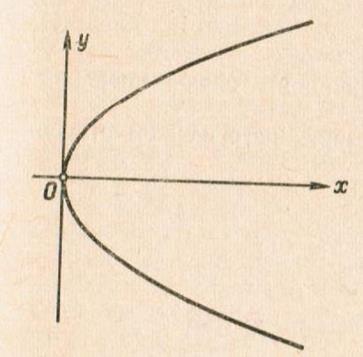
Рис. 177
Замечание. Уравнение 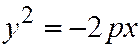 , где
, где 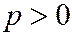 сводится к уравнению
сводится к уравнению 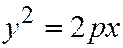 заменой
заменой 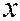 на
на 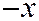 , т.е. путём преобразования системы координат, которое соответствует изменению положительного направления оси
, т.е. путём преобразования системы координат, которое соответствует изменению положительного направления оси 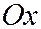 на противоположное.
на противоположное.
Отсюда следует, что парабола 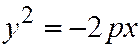 симметрична с параболой
симметрична с параболой 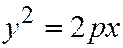 относительно оси
относительно оси 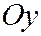 (См. рис.178). Аналогичными рассуждениями устанавливаем, что каждое из уравнений:
(См. рис.178). Аналогичными рассуждениями устанавливаем, что каждое из уравнений: 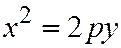 ;
; 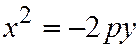 (2) где
(2) где 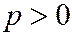 определяет параболу с вершиной в начале координат и осью симметрии
определяет параболу с вершиной в начале координат и осью симметрии  (См. рис. 179, 180).
(См. рис. 179, 180).
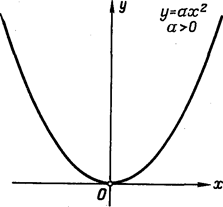
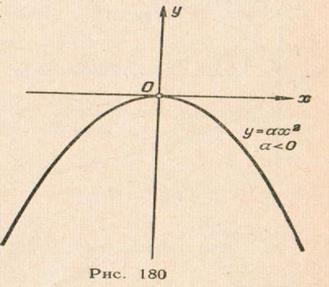
Рис. 179
Уравнение (2) пишут часто в виде, разрешённом относительно ординаты 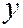 :
: 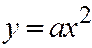 , где
, где 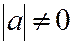 ; (
; ( 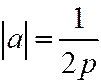 ).
).
Дата добавления: 2016-04-14; просмотров: 1258;
