Парабола и её каноническое уравнение

Определение. Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус и называемой директрисой.

Определение. Расстояние от фокуса параболы до её директрисы называется параметром параболы. Эксцентриситет параболы принимается равным единице.

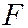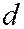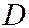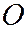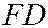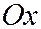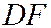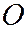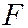Опустим из фокуса перпендикуляр на директрису и точку пересечения этого перпендикуляра с директрисой параболы обозначим буквой . Введём на плоскости ДПСК, поместив начало координат в центре отрезка , принимая за ось прямую , с положительным направлением от к (См. рис.176).

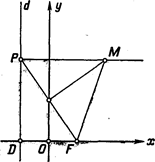
Рис. 176

Расстояние 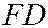от фокуса 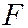до директрисы 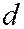обозначим буквой 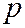(это параметр параболы). В выбранной системе координат фокус 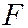имеет координаты 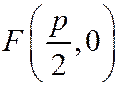. Уравнение директрисы .

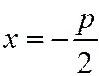Пусть 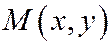- произвольная точка плоскости. Обозначим через 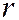расстояние 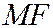от точки 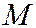до фокуса 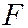параболы, а через 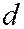- расстояние 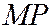от точки 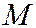до директрисы этой параболы.

Точка 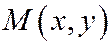лежит на данной параболе тогда и

только тогда, когда . Так как ,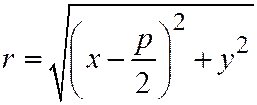

а 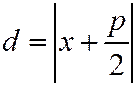, то уравнение параболы имеет вид:

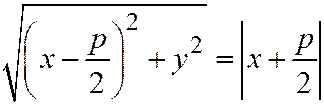. Это уравнение эквивалентно следующему уравнению: .

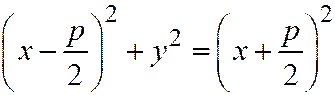Или: 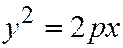(1)

Определение. Уравнение (1) называется каноническим уравнением параболы.