Определение и классификация

Числа отображаются с помощью системы счисления.

ж

Совокупность символов, при помощи которых записывается система счисления, называется алфавитом системы счисления. Количество символов, составляющих алфавит, называется его размерностью.

Системы счисления делятся на позиционные и непозиционные. В позици­онной системе счисления значение каждой цифры в записи числа зависит от ее позиции (разряда). В непозиционной системе счисления для обозначения чисел вводятся специальные знаки, количественное значение которых всегда одинако­во и не зависит от их места в записи числа, например, числу 25 в непозиционной римской системе счисления соответствует запись XXV, а числу 53 соответствует запись LIIL

Последовательность чисел, каждое из которых задает «вес» соответствующего разряда, называется базисом позиционной системы счисления. Основным досто­инством позиционной системы счисления является возможность записи произ­вольного числа при помощи ограниченного набора символов.

В табл. 11.4 сравниваются несколько двоичных и десятичных чисел, находящих­ся в одной и той же позиции.Обе эти системы счисления являются позиционными. Значение каждой цифры в числе легко определить, воспользовавшись формулой

V=Bⁿ.

Здесь V — значение, В — основание системы счисления, N- порядковый номер позиции.

Очевидно, что десятичная запись намного удобнее двоичной, поскольку более компактна. Так, в 6-й позиции в десятичной системе закодирован миллион, а в дво­ичной — только шестьдесят четыре. В двоичной системе представление чисел по­лучается весьма громоздким, но оно идеально для компьютера, так как не требует сложных инженерных и технологических решений.

Позиционную систему счисления называют традиционной, если ее базис об­разуют члены геометрической прогрессии, а значения цифр есть целые неот­рицательные числа. Знаменатель P геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основанием этой системы счисления. Традиционные системы счисления с основанием P иначе на­зывают Р-ичными.

Для того чтобы показать, в какой системе счисления записано число, после числа указывают основание в качестве нижнего индекса. Например IO₂- два в дво­ичной системе счисления, или 2₁₀ — два в десятичной системе счисления.

—I Римская

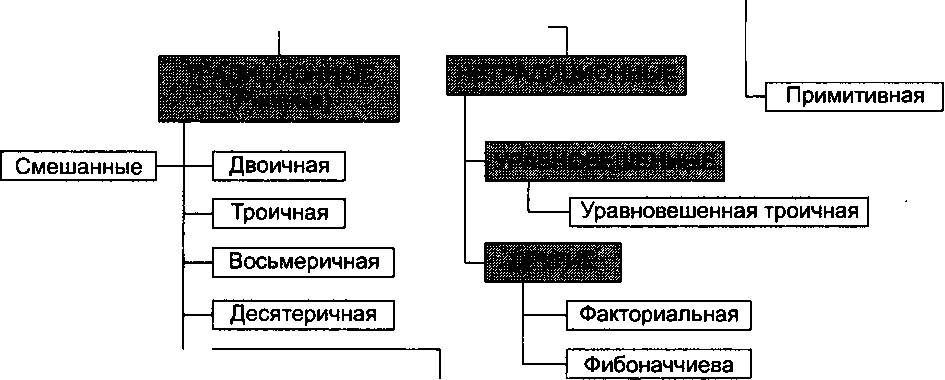
Если в позиционной системе счисления базис не является геометрической прогрессией или значения цифр могут принимать отрицательные значения, такую систему счисления называют нетрадиционной (рис. 11.4).

I Шестнадцатеричная Рис. 11.4. Системы счисления

Любое натуральное число можно записать в Р-ичной системе счисления един­ственным образом. В более строгом виде это утверждение можно сформулировать в следующем виде.

Пусть P — произвольное натуральное число, большее единицы. Существует единственное представление любого натурального числа X в виде степенного ряда:

Х = а_пР^п +а_п__хР^п~^х +... + а_хР + я₀, где O^a_i <Р, O^i^n.

В Р-ичной системе счисления любое неотрицательное вещественное число, со­держащее целую и дробную части, можно записать в виде

а = а_пР^п + а_п__хР^пА +... + а_хР + а₀ + а__хР~^х + а_₂Р~² +...= - ^a_iPⁱ, 0 ^a_i <Р, яг>0.

Здесь P > 0 — основание позиционной системы счисления, а_{ — цифры числа а в Р-ичной системе счисления.

Для записи чисел в Р-ичных системах счисления используют десятичные цифры (О... 9), которые дополняются буквами латинского алфавита.

В табл. 11.5 приведен пример того, как будет выглядеть число 25, записанное в разных Р-ичных системах счисления.

Для записи отрицательных чисел в Р-ичных системах счисления используют знак «минус», помещенный перед числом. При записи вещественных чисел для отделения дробной части числа от целой ставится запятая. Таким образом на за­пись Р-ичных чисел распространяются привычные нам по десятичной системе счисления правила, например: -2,2₁₀, -F,OE₁₆, -101,OOl₂.