Форма представления данных в компьютере

11.1.1. Общее представление

В каком виде хранится, как перерабатывается информация в мозгу человека, откуда появляется там еще одно нематериальное понятие, «смысл», в обозримом будущем наука вряд ли сможет достаточно аргументировано объяснить. А вот в каком виде информация хранится в компьютерах, что именно передается, коди­руется, декодируется, извлекается, переводится в сигналы и посылается человеку, мы знаем точно — это данные.

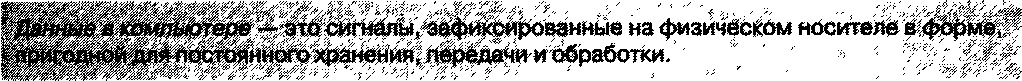
Приведенное определение данных достаточно широко, чтобы отнести его не только к хранению и обработке при помощи компьютера. Когда в древние века люди вели учет казны на глиняных табличках, у них не было компьютеров, но уже были данные, ибо они фиксировали информацию на физическом носителе, в форме, пригодной для постоянного хранения и использования. В наше время этот процесс претерпел значительные усовершенствования, причем как на стадии преоб­разования информации в данные, так и на стадии хранения и передачи. В качестве физического носителя теперь используются различного рода электронные и маг­нитные средства, для обработки данных применяются компьютеры, а для переда­чи — различного рода компьютерные сети и другие радиоэлектронные устройства.

В то же время смысловое отношение между понятиями «информация» и «дан­ные» сохраняется, и данные, как и много веков назад, по-прежнему являются физическим (материальным) носителем некоторых сигналов, которые становятся информацией только в момент осмысления их человеком.

Самым удобным представлением данных в компьютере оказалось представле­ние с помощью двоичной элементной базы в виде дискретных сигналов с двумя состояниями. Это связано с простотой распознавания и хранения на физическом уровне сигналов, имеющих только два состояния: «включен — выключен», «да — нет», «есть ток (потенциал) — нет тока (потенциала)».

Для хранения данных в компьютере используется ячейка памяти. Каждая ячейка памяти представляет собой физическую систему, состоящую из однородных элементов — битовых разрядов, каждый из которых может принимать одно из двух возможных значений: 0 или 1. Представление данных с помощью битовых разрядов получило название бинарного представления.

Минимальное количество битовых разрядов в одной ячейке памяти, к которой можно обратиться по адресу, равно 8. Ячейка памяти, состоящая из 8 битовых раз­рядов, получила название байта.

Справка. Исторически, для обозначения двоичного разряда употребляли слово­сочетание двоичная цифра (binary digit).

В 1948 г. американский математик Джон Уайлдер Таки Qohn Wilder Tukey) предложил заменить это словосочетание более коротким. После недолгого вы­бора между сокращением «bigit» и «binit», он пришел к слову bit (бит), которое не только хорошо сокращало «binary digit», но и имело значение в английском языке (bit — маленький кусочек, самая малая часть чего-либо). На самом деле бит — это самая малая мера информации и самая малая величина, при помощи которой информацию можно перевести в данные.

В течение одного такта генератора тактовой частоты центральный процессор может обратиться к одному, двум, четырем или восьми байтам информации. Ко­личество байтов информации, одновременно доступных центральному процессору, определяется количеством разрядов шины данных компьютера. Соответственно, про компьютеры говорят — 8-, 16-, 32- или 64-разрядный. На сегодняшний день среди персональных компьютеров большинство 32-разрядных, и в настоящее время происходит переход от 32-разрядных к 64-разрядным моделям.

Представление сигналов в любом другом, не двоичном, виде потребовало бы реализации ячеек для хранения информации, в которых каждый разряд обладал бы тремя состояниями и более. В этом случае недостаточно было бы распознавать только факт наличия или отсутствия тока (потенциала). Необходимо было бы еще измерять его уровень, что намного удорожало бы технологию производства таких вычислительных машин.

Технологические особенности производства электронных компонентов, дела­ющие двоичную элементную базу более дешевой, чем троичная, на долгое время отодвинули троичные машины на задний план. Возможно, в будущем компьютеры на троичной логике займут главенствующее положение в технологиях, однако се­годня об этом говорить не приходится. Однако можно с уверенностью утверждать, что представление данных в бинарном коде в недрах ЭВМ — не единственный вариант, и бинарность — всего лишь технологическая, а не информационная не­обходимость.

Таким образом, у всех современных компьютеров данные на физическом уровне представлены в двоичном (бинарном) виде.

Современные компьютеры способны при помощи специального оборудования воспринимать, преобразовывать в данные, хранить и воспроизводить следующие виды информации:

□ числовую;

□ символьную (текст);

□ звуковую, или аудио (голос, музыку, шумы);

□ графическую (рисунки, фотографии, чертежи, сканированные изображения);

□ видео (фильмы, видеозаписи).

Если сравнивать этот перечень с типами сигналов, которые могут воспринимать органы чувств человека, то вкус, запах и все, что называется «кинестетическими ощущениями» (ощущения веса, давления, положения в пространстве, прикосно­вения, боли), пока не получило соответствующего места в ряду обрабатываемой компьютером информации. Однако сегодня в этом направлении ведутся активные научные и технические разработки, и тот день, когда компьютер сможет хранить, обрабатывать и воспроизводить данные, несущие в себе кинестетическую инфор­мацию, не так уж далек.

Числовые данные

Числовые данные в компьютере представляются двумя подмножествами: це­лыми и действительными числами (числами с плавающей запятой). В отличие от символов, ввод числовых данных не может происходить прямым преобразованием и записью кодов, передаваемых с клавиатуры. С клавиатуры мы передаем последо­вательность символов. Эта последовательность затем программным образом пре­образуется в числа. Для того чтобы полученное число было выведено на экран, оно снова программным путем преобразуется в последовательность символов. В памяти компьютера число хранится в виде двоичного представления.

Целые числа, в зависимости от типа данных, хранятся в памяти компьютера, за­нимая один, два, четыре и более байта. Каждый бит в байте — это один двоичный разряд. В случае, когда число должно иметь знак, один из разрядов используется для хранения знака. В табл. 11.1 показаны варианты целочисленных представлений с разным числом байтов.

Как видите, даже 32-разрядного целочисленного представления, как со знаком, так и без, вполне достаточно для решения большинства задач.

Теоретически в памяти компьютера представление отрицательного целого числа может храниться в прямом, обратном или дополнительном коде. Предположим, нам надо представить в двоичном виде целое число 7. Без знака оно поместится в 8-разрядную ячейку следующим образом:

Если это десятичное число -7 (минус семь), то его прямое представление будет выглядеть так:

1 0 0 0 0 1 1 1

То есть старший бит призван показать, что это число со знаком «минус».

Однако на практике отрицательные числа не хранятся в виде прямого кода, а всегда приводятся к дополнительному коду. Этот код получается из прямого следующим образом: все разряды, кроме знакового, инвертируются (то есть вме­сто единиц подставляются 0, вместо нулей — единицы). Так число превращается в обратный код. Затем к результату прибавляется единица, и код становится до­полнительным. Вот так будет выглядеть дополнительный код для числа -7:

Дополнительный код используется для уменьшения количества циклов, за которые процессор выполняет арифметические операции над этими числами, по­скольку позволяет заменить операцию вычитания операцией сложения.

Действительные числа состоят из двух частей: мантиссы и порядка. Ман­тисса — это целое число, содержащее только значащие цифры исходного числа, а порядок — это позиция запятой, разделяющей целую и дробную части числа. Например, если в памяти надо сохранить число 00313,560, то записаны будут два целых числа: 31356 и 3.

При хранении действительных чисел возникает проблема: некоторые действия над числами приводят к потере точности.

Пример. При делении 1 на 3 результатом является бесконечная иррациональная дробь: 0,3333... Поскольку место в памяти, отведенное под запись этого числа, не бесконечно, то в определенном месте повторение троек придется остановить и записать в память округленное число. Это, в свою очередь, значит, что при умножении такой дроби на три уже не получится результат, равный единице, то есть происходит потеря точности.

Символьные данные

Символьные данные, которые несут в себе текстовую информацию, попадают в компьютер наиболее простым из всех известных способов: после нажатия клави­ши на клавиатуре генерируется один байт данных, который записывается в память компьютера. Каждой клавише компьютера соответствует одно определенное со­четание битов в байте. Поскольку битов в байте 8, то общее количество сочетаний, которое может быть получено в результате различных комбинаций нулей и единиц внутри байта, равно 256 (2⁸). Например, 10 нажатий клавиш создает в памяти ком­пьютера последовательность из 10 заполненных байтов. Таков процесс поступления в компьютер и хранения в компьютере простого текста.

Любая из комбинаций битов в байте может рассматриваться как число, за­писанное в двоичном коде. Соответствие числа, которое при нажатии клавиши записывается в память компьютера, и символа, который появляется на экране при воспроизведении данного числа в символьном виде, называется кодовой таблицей. По мере развития компьютерной техники потребность во все более полном ото­бражении символьной (текстовой) информации возрастала. Вначале казалось, что для кодирования символов при помощи чисел с избытком хватит 127 байт. Первое по порядку 31 десятичное число было отдано под служебные символы (перевод строки, перевод каретки, звонок, пустой символ) (табл. 11.2). Следующие по по­рядку числа (от 32 до 127) кодировали символы алфавита (табл. 11.3).

Этой таблицы символов вполне хватило для ввода символьной информации на английском языке, и она стала стандартом ASCII (American Standard Code for Information Interchange — американский стандартный код для обмена информа­цией).

Для кодирования символов, отличных от символов английского алфавита, была использована вторая часть из 256 комбинаций, числа от 128 до 256. Эта часть полу­чила название расширенной таблицы ASCII и может содержать в себе символы того или иного национального алфавита. При этом если первая часть таблицы ASCII сформирована один раз и не меняется, то вторая ее часть изменяется в зависимости от того, в какой операционной системе вы работаете. Буквы алфавита остаются теми же самыми, а связанные с ними числа меняются. Так, только для русского языка появились кодировки СР-866 (MS-DOS), СР-1251 (Windows), KOI8-R (UNIX и Linux). Именно наличие нескольких кодовых таблиц для одного и того же языка является причиной появления на интернет-страницах потоков странных иероглифов вместо обычного текста: программа просмотра Интернета не всегда способна определить, какую кодовую таблицу выбрать.

Даже если отвлечься от проблем с путаницей между разными кодовыми табли­цами одного и того же языка, кодирование многоязыковых текстов наталкивается на еще одно препятствие: Что делать, если в одном тексте встречаются фрагменты, написанные на разных языках? Что делать, если текст необходимо совместить с математическими или химическими формулами? Для решения этой проблемы способ кодирования символов еще раз изменили — один символ стали кодировать не одним, а двумя байтами данных. Так появился способ кодирования UNICODE. Теперь в одном байте можно было хранить код символа, а во втором указывать, из какой кодовой таблицы этот символ извлекать.

Таким образом, текстовая информация в компьютере может быть представлена как однобайтной последовательностью, когда каждый символ кодируется одним байтом в памяти компьютера, так и двухбайтной, требующей вдвое больше памяти для хранения, но зато более универсальной и гибкой.