Модели представления знаний
Существуют десятки моделей (или языков) представления знаний для различных предметных областей. Большинство из них может быть сведено к следующим классам:
□ продукционные модели;
□ семантические сети;
□ фреймы;
□ формальные логические модели.
Продукционная модель — модель, основанная на правилах, представляющих знания в виде предложений типа: если (условие), то (действие). База знаний при использовании продукционной модели представляет собой совокупность такого рода правил, записанных на формальном языке.
Под условием понимается некоторое предложение-образец, по которому осуществляется поиск в базе знаний, а под действием — операции, выполняемые при успешном исходе поиска. Действия могут быть промежуточными, выступающими далее как условия, и терминальными, или целевыми, завершающими работу системы.
Программа, управляющая перебором правил, называется машиной вывода. Чаще всего вывод бывает прямой (от данных к поиску цели) или обратный (от цели для ее подтверждения — к данным). Данные — это исходные факты, на основании которых запускается машина вывода — программа, перебирающая правила из базы.
Пример. Имеется фрагмент базы знаний из двух правил, первого (П1) и второго (П2):
П1: Если «котировки на акции падают» и «состояние рынка нестабильное», то «покупать».
П2: Если «биржевые индексы падают», то «состояние рынка нестабильное». Предположим, в систему поступили данные — «котировки на акции падают» и «биржевые индексы падают».
Прямой вывод — исходя из данных, получить ответ. Первый проход.
Шаг 1. Пробуем П1, не работает (не хватает данных «состояние нестабильное»). Шаг 2. Пробуем П2, работает, в базу поступает факт «состояние нестабильное». Второй проход.
ШагЗ. Пробуем П1, работает, активируется цель «покупать», которая и выступает как совет, который дает ЭС.
Обратный вывод — подтвердить выбранную цель при помощи имеющихся правил и данных.
Первый проход.
Шаг 1. Цель — «покупать»: пробуем П1 — данных «состояние нестабильное» нет, они становятся новой целью, и ищется правило, где цель в правой части.
Шаг 2. Цель «состояние нестабильное»: правило П2 подтверждает цель и активирует ее.
Второй проход.
ШагЗ. Пробуем П1, подтверждается искомая цель.
Продукционная модель чаще всего применяется в промышленных экспертных системах. Она привлекает разработчиков своей наглядностью, высокой степенью модульности, легкостью внесения дополнений и изменений, простотой механизма логического вывода.
3.3.1. Семантические сети
Термин «семантическая» означает «смысловая», а сама семантика — это наука, устанавливающая отношения между символами и объектами, которые они обозначают, то есть наука, определяющая смысл знаков.

|
Можно ввести несколько классификаций семантических сетей. Например, по количеству типов отношений:
□ однородные — с единственным типом отношений;
□ неоднородные — с различными типами отношений. По типам отношений:
□ бинарные, в которых отношения связывают два объекта;
□ w-арные, в которых есть специальные отношения, связывающие более двух понятий.
Наиболее часто в семантических сетях используются следующие отношения:
□ связи типа «часть—целое» («класс—подкласс», «элемент—множество» и т. п.);
□ функциональные связи (определяемые обычно глаголами «производит», «влияет», «любит»...);
□ количественные связи («больше», «меньше», «равно»...);
□ пространственные связи («далеко от», «близко от», «за», «под», «над»...);
□ временные связи («раньше», «позже», «в течение»...);
□ атрибутивные связи («иметь свойство», «иметь значение»...);
□ логические связи («и», «или», «не») и др.
Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети (подсети), соответствующей поставленному вопросу.
Пример. На рис. 3.3 изображена семантическая сеть. В качестве вершин используются понятия: Подразделение, ОГЭ (отдел главного энергетика), Лифт, Отис, Подъемный механизм, Двигатель, Человек, Вместимость.
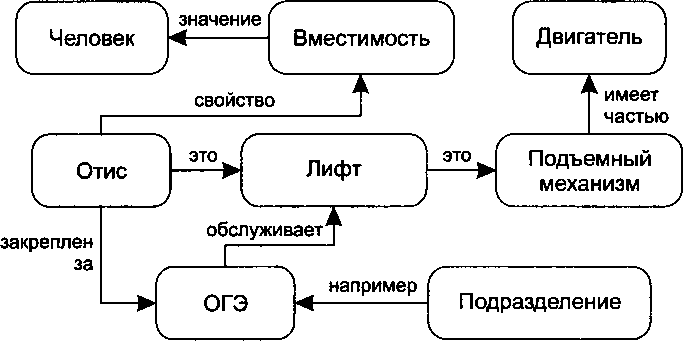 Рис. 3.3. Семантическая сеть
Рис. 3.3. Семантическая сеть
|
Основное преимущество этой модели — в ее соответствии современным представлениям об организации долговременной памяти человека. Недостаток модели — сложность поиска вывода.
3.3.2. Фреймы
Фрейм (от англ. frame — каркас, или рамка) предложен М. Минским в 70-е гг. как структура знаний, предназначенная для восприятия пространственных сцен. Эта модель, как и семантическая сеть, имеет глубокое психологическое обоснование.

|
Свойства, характеризующие описываемый объект или ситуацию, в случае фреймовой модели именуются слотами. Каждый слот имеет название, и ему может быть присвоено значение.
Структуру фрейма можно представить так: ИМЯ ФРЕЙМА:
(имя 1-го слота: значение 1-го слота), (имя 2-го слота: значение 2-го слота),
(имя N-го слота: значение N-го слота).
Ту же запись можно представить в виде таблицы, дополнив двумя столбцами:
| Имя фрейма | |||
| Имя слота | Тип слота | Значение слота | Присоединенная процедура |
В таблице дополнительные столбцы предназначены для описания типа слота и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов. В качестве значения слота может выступать имя другого фрейма — так образуют сети фреймов.
Различают фреймы-образцы, или прототипы, хранящиеся в базе знаний, и фреймы-экземпляры, которые создаются для отображения реальных ситуаций на основе поступающих данных. У фреймов-образцов все слоты или часть их не имеют значений, у фреймов-экземпляров все слоты заполнены значениями, описывающими конкретный объект, сценарий, ситуацию или роль.
Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через
□ фреймы-структуры (обозначают объекты и понятия, такие как заем, залог, вексель);
□ фреймы-роли (менеджер, кассир, клиент);
□ фреймы-сценарии (банкротство, собрание акционеров, празднование именин);
□ фреймы-ситуации (тревога, авария, рабочий режим устройства) и др.
Важнейшим в теории фреймов является наследование свойств, заимствованное из теории семантических сетей. И во фреймах, и в семантических сетях наследование происходит по АКО-связям (от англ. A Kind Of — это). Слот AKO указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются (то есть переносятся) значения аналогичных слотов.
Пример. В сети фреймов на рис. 3.4 понятие «программист» наследует свойства фреймов «инженер» и «служащий», которые находятся на более высоком уровне иерархии. Так, на вопрос: «Есть ли у инженера табельный номер?» — следует ответ: «Да», так как этим свойством обладают все служащие, что указано во фрейме «служащий». Таким образом, иерархическая связь между фреймами осуществляется через значение, указанное в слоте АКО.
Служащий
Инженер
| AKO Человек |
| Программист AKO |
| Табельный номер |
| Инженер |
| 14-031 |
АКО[Служащий Служба
Главного инженера
Отдел рРазработкй"
| Область |
Ком п. техника
Знает .NET, JAVA
Образование | Высшее"
|
Ф. И. О. Петров И. П.
Рис. 3.4. Сеть фреймов
Основным преимуществом фреймов в качестве модели представления знаний является способность отражать концептуальную основу организации памяти человека, можно также отметить ее гибкость и наглядность.
3.3.3. Формальные логические модели
Традиционно в представлении знаний выделяют формальные логические модели. основанные на классическом исчислении предикатов I порядка. Предикат — это то, что утверждается или отрицается о субъекте суждения.
Пример. Мы можем обозначить предикатом РАВНО(х,г/) отношение равенства (х = у), где х и у принадлежат множеству вещественных чисел. В этом случае предикат РАВНО будет принимать значение ИСТИНА для всех равных значений х и у.
Связывая между собой предикаты при помощи символов математической логики, можно описывать сложные логические высказывания на формальном языке. Для того, чтобы на основе исчисления предикатов создавать компьютерные модели, разработаны специальные языки логического программирования (одним из них является prolog).
Описание этих моделей опустим, так как исчисление предикатов I порядка в промышленных экспертных системах практически не используется. Эта логическая модель применима в основном в исследовательских «игрушечных» системах, так как предъявляет очень высокие требования и ограничения к предметной области.
В промышленных же экспертных системах используются различные ее модификации и расширения, изложение которых выходит за рамки темы данного учебника.
Дата добавления: 2016-04-14; просмотров: 1394;
