Алгоритмы обработки результатов измерений, полученных в разных сериях или различными методами.
НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ
Измерения называют равноточными, если они выполнены при одинаковых условиях . Наиболее надежным результатом из ряда результатов равноточных измерений является среднее арифметическое.
Но не менее часто встречаются случаи, когда одна и та же величина измеряется при различных условиях. Такие измерения называются неравноточными.
Если имеется ряд неравноточных измерений х1, х2, ..., хn одной и той же величины X, то для получения из них наиболее надежного значения этой величины нельзя взять просто среднее арифметическое. Очевидно, что измерение более точное должно иметь и большее влияние на окончательный результат. Неравноточные измерения одной и той же величины могут иметь место в силу следующих причин:
1. Из-за использования средств измерений различной точности;
2. Из-за выполнения измерений при разных условиях внешней
среды;
3. Из-за различного числа измерений одним и тем же средством
измерений при необходимости каждый раз взять из них среднее
арифметическое;
4. Из-за проведения измерений одним средством измерений, но
различными операторами.
В силу отмеченного, возникает необходимость объединения результатов, отличного от ранее рассмотренного. Оценка искомого значения измеряемой величины в этом случае осуществляется при помощи так называемого весового среднего арифметического значения (хр).
Простейшим случаем неравноточных измерений являются несколько групп равноточных измерений, число измерений в каждой группе различно.
Пусть произведено m1 равноточных измерений, из которых выведено наиболее вероятное значение х1 измеряемой величины. Другая серия таких же измерений содержала m2 измерений и дала значение х2, третья –m3 измерений и дала значение х3 и т. д.Ставится задача вывести наиболее вероятное значение измеряемой величины на основании результатов. Для решения этой задачи используется понятие «вес».
ОБЩИЕ СВЕДЕНИЯ О ПОНЯТИИ «ВЕС»
Вес является вспомогательным числом при совместной обработке неравноточных или разнородных измерений.
Если σ — средняя квадратическая погрешность результата измерения, то вес этого результата находят по формуле
Pi =μ2/ σ2i
где μ — коэффициент пропорциональности.
Это понятие веса для измеренной величины принято и для любой функции F измеренных величин; вес РF функции F при известной средней квадратической погрешности σ F вычисляют по формуле
PF =μ2/ σ2F
Веса результатов измерений и их функции являются положительными числами, пропорциональными квадратам их средних квадратических погрешностей (дисперсиям).
Если Pi =1, то при однородных неравноточных измерениях будем иметь μ = σi
Рассмотрим некоторые случаи, приводящие к необходимости проведения и обработки неравноточных измерений.
1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и нет признаков систематических погрешностей, то при объединении всех полученных результатов и на основе их математической обработки получают более достоверные сведения об измеряемой величине.
2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Используя все имеющиеся данные, пытаются получить более достоверные значения измеряемых величин.
3. Измерения одних и тех же величин могут повторяться через определенное время. В итоге появляется необходимость объединения результатов. Точность рядов различна.
Во всех этих случаях приходится прибегать к методам обработки результатов неравноточных измерений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений.
Веса при неравноточныхъ измерениях вводятся по следующей формуле:
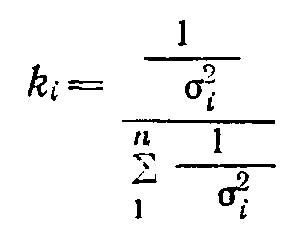
Тогда средневзвешенная величина определится по следующей формуле:
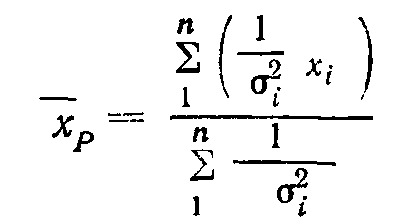
И дисперсия весового среднего определяется формулой
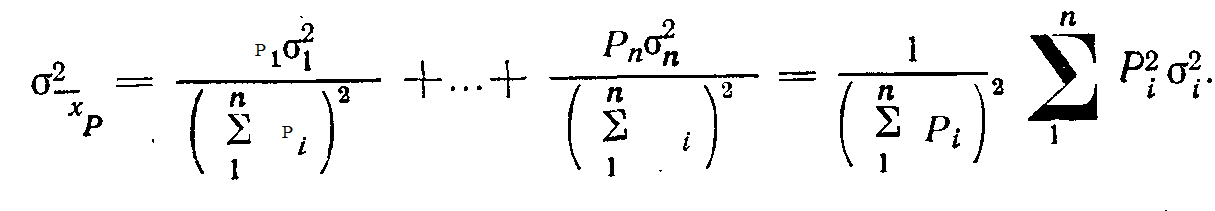
где ki = Pi
Так как 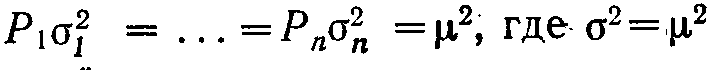 то можно получить следующее выражение для дисперсии
то можно получить следующее выражение для дисперсии
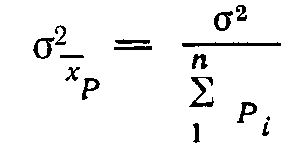



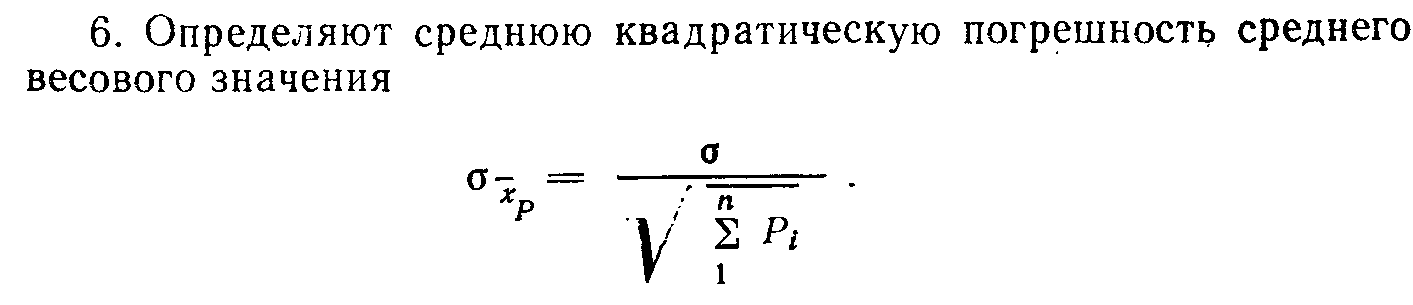

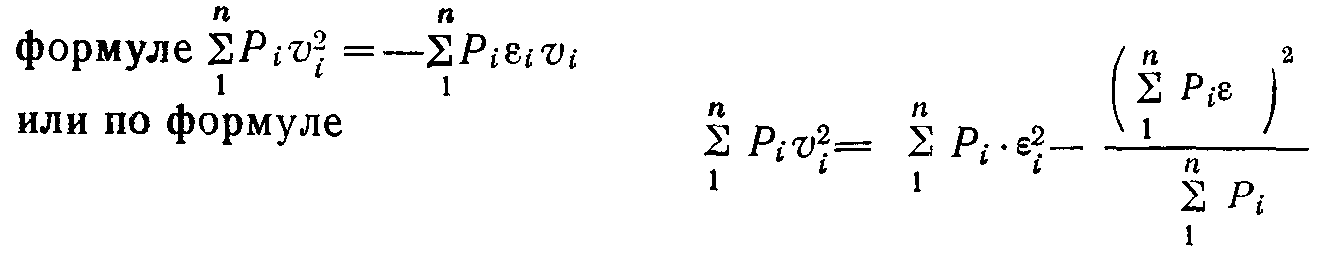




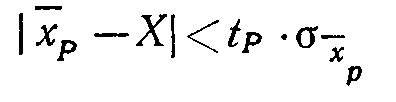
Дата добавления: 2016-04-14; просмотров: 2825;
