Обработка результатов совместных измерений на основе метода наименьших квадратов.
Совместные измерения представляют собой производимые одновременно измерения двух или нескольких, как правило, неодноименных величин для нахождения зависимости между ними. Этот вид измерений находит широкое применение в научных, технических и метрологических измерениях. Совместные измерения применяются в метрологической практике при экспериментальном определении градуировочных характеристик средств измерений, в том числе различных преобразователей.
При этом считают, что выполняются следующие условия:
1) значения входных величин xi известны точно;
2) результаты измеренных выходных величин yi содержат независимые случайные погрешности, которые распределены по нормальному закону.
3. Резко выделяющиеся значения (промахи) должны быть исключены.
В общем случае, если характер зависимости неизвестен, то лучше всего сглаживание проводить полиномами n-степени:
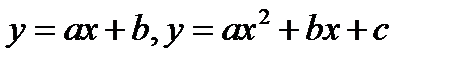 …..
…..
В области обработки результатов измерений используется метод наименьших квадратов.
Пусть проводится изучение зависимости:
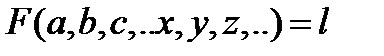
Если в это уравнение подставить результаты измеренных значений x,y,z,..l то получим систему уравнений:
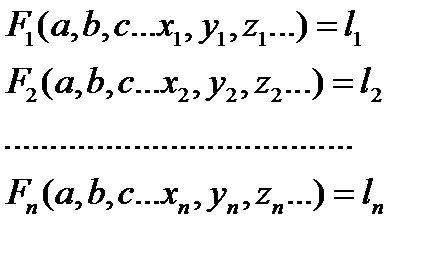
Поскольку уравнения неточны, то можем записать:
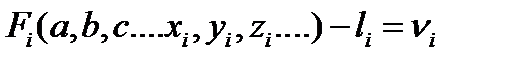
И после этого выбираются такие значения a,b,c…чтобы минимизировать сумму квадратов остаточных погрешностей:
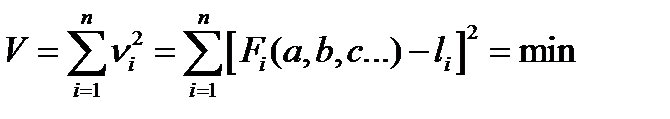
Очевидно, что минимум достигается, когда :
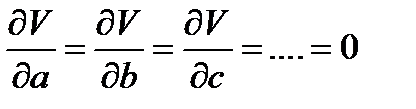
Полученная система уравнений позволяет определить наилучшие оценки искомой величины, а дисперсия будет:
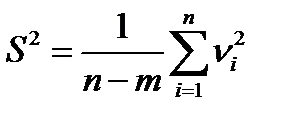
Дата добавления: 2016-04-14; просмотров: 2011;
