Крутящий момент многопластинчатого гидромотора однократного действия

Крутящий момент, который развивается многопластинчатым гидромотором однократного действия, равняется разнице моментов сил давления рабочей жидкости на две пластины, которые находятся у противоположных перевальных перемычек (рис. 7.12).

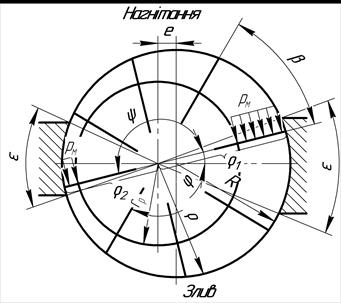
а)

б)

Рис. 7.12. Схемы к определению крутящего момента многопластинчатого гидромотора однократного действия: а) – с четным числом пластин; б) – с нечетным числом пластин

Крутящие моменты, которые развиваются силой давления рабочей жидкости:

- на выдвинутой (правой, рис. 7.12) пластине

;

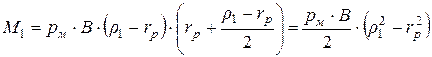- на утопленной (левой) пластине

,

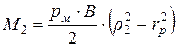где 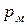- давление гидромотора;

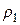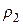и - текущие расстояния (радиусы) от центра вращения ротора к статорному кольцу в пределах соответствующих перевальных перемычек.

Теоретический крутящий момент, который развивается многопластинчатым гидромотором однократного действия, равняется

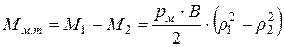. (7.25)

Пренебрегая изменением текущих радиусов 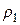и 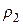в пределах соответствующих перевальных перемычек и приняв для этого случая и 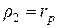, откуда 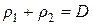и , выражение (7.25) можно представить следующим образом

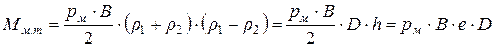. (7.26)

Так как рабочий объем многопластинчатого гидромотора однократного действия без учета толщины пластин определяется как и рабочий объем многопластинчатого насоса однократного действия, то есть с использованием (7.11), то из (7.26) средний теоретический крутящий момент гидромотора составляет

.

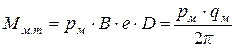Для получения зависимости текущего крутящего момента от угла поворота ротора 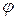определим радиусы 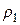и 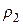по аналогии с (7.6) следующим образом

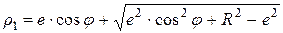; (7.27)

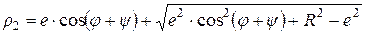, (7.28)

где 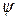- угол между радиусам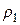и и 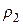(рис. 7.12).

Представим (7.27) и (7.28) в виде

;

,

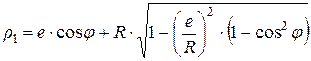откуда с учетом 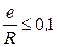и допустимой погрешностью можно записать

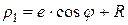; (7.29)

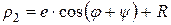. (7.30)

Подставив (7.29) и (7.30) в (7.25), получим зависимость текущего крутящего момента многопластинчатого гидромотора однократного действия от угла поворота ротора

. (7.31)

Для гидромоторов с четным числом пластин 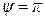, и уравнение (7.31) принимает вид

. (7.32)

Для гидромоторов с нечетным числом пластин с учетом 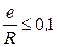и допустимой погрешностью уравнение (7.31) принимает вид

,

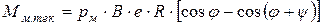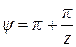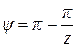где при , при .

Таким образом, текущий крутящий момент многопластинчатого гидромотора однократного действия изменяется по закону косинуса при изменении угла поворота ротора в пределах , где .

Для гидромотора с четным числом пластин в соответствии с (7.32) текущий крутящий момент принимает значение:

- максимальное - при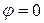

;

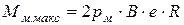- минимальное - при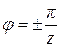

.

Неравномерность крутящего момента многопластинчатого гидромотора однократного действия, которая обусловлена закономерностями геометрического изменения объемов рабочих камер, оценивается коэффициентом неравномерности

. (7.33)

С учетом ряда допущений [21] уравнение (7.33) принимает вид:

- для гидромоторов с четным числом пластин

;

- для гидромоторов с нечетным числом пластин

,

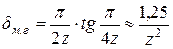то есть неравномерность крутящего момента многопластинчатого гидромотора однократного действия соответствует неравномерности подачи многопластинчатого насоса однократного действия (7.18), (7.19).

Таким образом, неравномерность крутящего момента гидромотора с нечетным числом пластин значительно меньше соответствующей неравномерности гидромотора с четным числом пластин при том, что и в первом и во втором случаях коэффициенты неравномерности обратно пропорциональные квадрату числа пластин. То есть, для уменьшения неравномерности крутящего момента многопластинчатого гидромотора однократного действия необходимо увеличивать количество пластин при общем нечетном их числе в гидромашине.

Другие факторы, которые влияют на равномерность крутящего момента гидромотора аналогичны тем, которые рассматривались при анализе равномерности подачи многопластинчатых насосов однократного действия (раздел 7.3.2).