Интерференция на тонких пленках
Интерференция в проходящем свете. Осветим тонкую прозрачную пленку (например, мыльную) с абсолютным показателем преломления п светом, длина волны которого в вакууме l. Будем
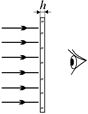 Рис. 19.12
Рис. 19.12
| смотреть на пленку с противоположной стороны (рис. 19.12), т. е. будем наблюдать свет, проходящий через пленку. Выясним, при каком значении толщины пленки h будет наблюдаться максимум освещенности, а при каком – минимум. Читатель: Честно говоря, не очень понятно, почему здесь должна возникнуть интерференция? Автор: Дело в том, что некоторые лучи просто проходят пленку насквозь, а некоторые отражаются от |
 Рис. 19.13
Рис. 19.13
|
границы «пленка–воздух», идут назад, снова отражаются от границы «воздух–пленка» и лишь после этого выходят наружу (рис. 19.13). (Конечно, найдутся лучи, которые испытают несколько пар отражений, но их доля в общем «балансе» будет не так велика, ведь часть световых волн будет уходить обратно, т.е. туда, откуда пришли.)
Интерференция будет проходить между лучом (правильнее сказать, конечно, световой волной) 1¢ и лучом 2¢. Геометрическая разность хода этих лучей (разность длин пройденных путей) равна Ds = 2h. Оптическая разность хода D = пDs = 2пh.
Условие максимума
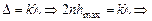
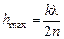 ; (19.8)
; (19.8)
Условие минимума
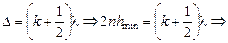
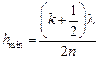 . (19.9)
. (19.9)
Если в формуле (19.9) положить k = 0, получим 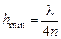 , именно при такой длине наступает первый минимум освещенности в проходящем свете.
, именно при такой длине наступает первый минимум освещенности в проходящем свете.
Интерференция в отраженном свете.Рассмотрим ту же самую пленку с противоположной стороны (рис. 19.14). В данном случае мы будем наблюдать интерференцию за счет взаимодействия лучей 1¢ и 2¢: луч 1¢ отразился от границы «воздух–пленка», а луч 2¢ – от границы «пленка–воздух» (рис. 19.15).
Рис. 19.14 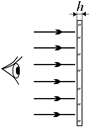 Рис. 19.15
Рис. 19.15 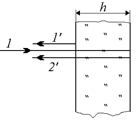
Читатель: По-моему, здесь ситуация точно такая же, как и с проходящим светом: Ds = 2h; D = пDs = 2nh, а для hmax и hmin справедливы формулы (19.8) и (19.9).
Автор: Значит, при 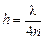 мы будем иметь минимум освещенности в отраженном свете?
мы будем иметь минимум освещенности в отраженном свете?
Читатель: Да.
Автор: И минимум в проходящем? Получается, что свет войдет в пленку, а наружу не выйдет, так как и спереди, и сзади – минимум освещенности. Куда же делась световая энергия, если пленка не поглощает света?
Читатель: Да, такое, действительно, невозможно. Но где же ошибка?
Автор: Тут необходимо знать один экспериментальный факт. Если световая волна отражается от границы среды более оптически плотной с менее оптически плотной (стекло–воздух), то фаза отраженной волны равна фазе падающей (рис. 19.16, а). А вот если отражение проходит на границе среды, оптически менее плотной, со средой, более плотной (воздух–стекло), то фаза волны уменьшается на p (рис. 19.16, б). А это значит, что оптическая разность хода уменьшается на половину длины волны 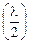 , т.е. луч 1¢, отраженный от внешней поверхности пластины (см. рис. 19.15), «теряет» полволны, и за счет этого отставание от него второго луча в оптической разности хода уменьшается на l/2.
, т.е. луч 1¢, отраженный от внешней поверхности пластины (см. рис. 19.15), «теряет» полволны, и за счет этого отставание от него второго луча в оптической разности хода уменьшается на l/2.
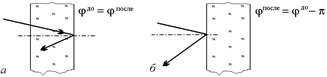
Рис. 19.16
Таким образом, оптическая разность хода лучей 2¢ и 1¢ на рис. 19.15 будет равна
 .
.
Тогда условие максимума запишется в виде

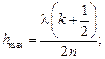 (19.10)
(19.10)
условие минимума
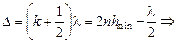
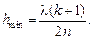 (19.11)
(19.11)
Сравнивая формулы (19.8) и (19.11), (19.9) и (19.10), видим, что при одном и том же значении h достигается минимум освещенности в проходящем свете и максимум в отраженном или же максимум в проходящем и минимум в отраженном. Иными словами, свет либо главным образом отражается, либо проходит насквозь в зависимости от толщины пленки.
Задача 19.5. Просветление оптики. Чтобы уменьшить долю отраженного света от оптических стекол (например, от объективов фотоаппарата) на их поверхность наносят тонкий слой прозрачного вещества, у которого показатель преломления п меньше, чем у стекла (так называемый метод просветления оптики). Оцените толщину нанесенного слоя, считая, что лучи падают на оптическое стекло приблизительно нормально (рис. 19.17).
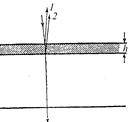 Рис. 19.17
Рис. 19.17
|
Решение. Для уменьшения доли отраженного света необходимо, чтобы лучи 1 и 2 (см. рис. 19.17), отраженные от внешней и внутренней поверхности пленки, соответственно «гасили» друг друга.
Заметим, что оба луча при отражении от более оптически плотной среды теряют по полволны каждый. Поэтому оптическая разность хода будет равна D = 2nh.
Условие минимума будет иметь вид
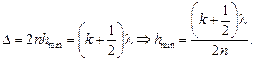
Минимальная толщина пленки hmin, соответствующая k = 0,
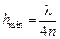 .
.
Оценим величину hmin. Возьмем l = 500 нм, п = 1,5, тогда
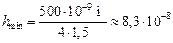 м = 83 нм.
м = 83 нм.
Заметим, что при любой толщине пленки погасить на 100 % можно только свет определенной длины волны (при условии отсутствия поглощения!). Обычно «гасят» свет средней части спектра (желтый и зеленый). Остальные цвета при этом гасятся значительно слабее.
Читатель: А чем объяснить радужную окраску пленки бензина в луже?
Автор: Здесь тоже имеет место интерференция, как при просветлении оптики. Поскольку толщина пленки в разных местах различно, то в одном месте гасятся одни цвета, а в других – другие. «Непогашенные» цвета мы и видим на поверхности лужи.
СТОП! Решите самостоятельно: В6, С1–С5, D1.
Кольца Ньютона
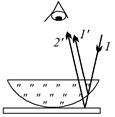 Рис. 19.18
Рис. 19.18
|
Задача 19.6. Рассмотрим подробно уже описанный нами опыт (рис. 19.18): на плоской стеклянной пластине лежит плосковыпуклая линза радиусом R. Сверху на линзу падает свет с длиной волны l. Свет является монохроматичным, т.е. длина волны жестко фиксирована и не меняется со временем. При наблюдении сверху видна интерференционная картина из концентрических светлых и темных колец (кольца Ньютона). При этом по мере удаления от центра кольца становятся более узкими. Требуется найти радиус N-го темного кольца (считая от центра).
| R N l | Решение. Интерференция возникает за счет наложения луча 1¢, отраженного от нижней поверхности линзы, и луча 2¢, отраженного от стеклянной пластины (см. рис. 19.18). Сначала решим чисто геометрическую задачу: по данным величинам R и r вычислим величину отрезка h |
| rN = ? | |
(рис. 19.19). Именно этот отрезок определяет геометрическую разность хода лучи 1¢ и 2¢.
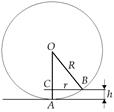 Рис. 19.19
Рис. 19.19
|
Рассмотрим DОВС:  (по теореме Пифагора),
(по теореме Пифагора),
h = АC = ОА – ОС =  . (1)
. (1)
Попробуем немного упростить выражение (1), учитывая, что r << R. Действительно, эксперименты показывают, что если R ~ 1 м, то r ~ 1 мм. Умножим и разделим выражение (1) на сопряженное выражение 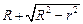 , получим
, получим

Запишем условие минимума для отраженного света: геометрическая разность хода лучей 1¢ и 2¢ составляет 2h, но луч 2¢ теряет полволны за счет отражения от оптически более плотной среды – стекла, поэтому оптическая разность хода получается на полволны меньше, чем геометрическая разность хода:
 .
.
Нас интересует радиус N-го темного кольца. Правильнее сказать, речь идет о радиусе окружности, в которой достигается N-й по счету от центра минимум освещенности. Если rN – искомый радиус, то условие минимума имеет вид:

где N = 0, 1, 2…
Запомним:
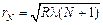 . (19.12)
. (19.12)
Кстати, при N = –1 r0 = 0. Это значит, что в центре будет находиться темное пятно.
Ответ: 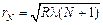
Заметим, что, зная rN, R и N, можно экспериментально определить длину волны света!
Читатель: А если бы нас интересовал радиус N-го светлого кольца?
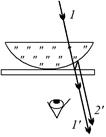 Рис. 19.20
Рис. 19.20
|
Автор: Тогда надо было бы воспользоваться условием максимума: D = lN.
Читатель: А можно ли наблюдать кольца Ньютона в проходящем свете?
Автор: Можно! Только учтите, что в этом случае луч 2¢ (рис. 19.20) два раза потеряет по полволны, т.е. потеряет целую волну.
СТОП! Решите самостоятельно: А7, В7, С6–С9, D2, D3.
Интерференция от двух щелей (опыт Юнга)
Английский ученый Томас Юнг (1773–1829) в 1807 г. поставил следующий опыт. Яркий пучок солнечного света он направил на экран с малым отверстием или узкой щелью S (рис. 19.21). Свет, прошедший через щель S, шел ко второму экрану с двумя узкими отверстиями или щелями S1 и S2.
 Рис. 19.21
Рис. 19.21
Щели S1 и S2 представляют собой когерентные источники, так как они имели «общее происхождение» – щель S. Свет от щелей S1 и S2 падал на удаленный экран, и на этом экране наблюдалось чередование темных и светлых участков.
Разберемся с этим опытом подробно. Будем считать, что S1 и S2 представляет собой длинные узкие щели, которые являются когерентными источниками, испускающими световые волны. На рис. 19.21 показан вид сверху.
 Рис. 19.22
Рис. 19.22
|
Область пространства, в которой эти волны перекрываются, называется полем интерференции. В этой области наблюдается чередование мест с максимальной и минимальной освещенностью. Если в поле интерференции внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. В объеме это выглядит так, как показано на рис. 19.22.
Пусть нам задана длина волны l, расстояние между источниками d и расстояние до экрана l. Найдем координаты хmin и хmax темных и светлых полос. Точнее, точки, соответствующие минимуму и максимуму освещенности. Все дальнейшие построения будем проводить в горизонтальной плоскости a, на которую будем «смотреть сверху» (рис. 19.23).
Рис. 19.23 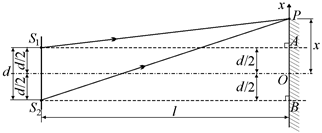
Рассмотрим точку Р на экране, находящуюся на расстоянии х от точки О (точка О – это пересечение экрана с перпендикуляром, восстановленным из середины отрезка S1S2). В точке Р налагаются друг на друга луч S1P, идущий от источника S1, и луч S2P, идущий от источника S2. Геометрическая разность хода этих лучей равна разности отрезков S1P и S2Р. Заметим, что поскольку оба луча распространяются в воздухе и не испытывают никаких отражений, то геометрическая разность хода равна оптической разности хода:
D = S2P – S1Р.
Рассмотрим прямоугольные треугольники S1АР и S2ВР. По теореме Пифагора: 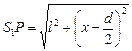 ,
, 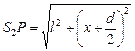 . Тогда
. Тогда
 .
.
Умножим и разделим выражение это выражение на сопряженное выражение, получим:
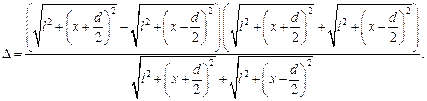
Учитывая, что l >> x и l >> d, упростим выражение



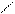

Итак:  .
.
Условие максимума:

 , (19.13)
, (19.13)
где k = 0, 1, 2, …
Условие минимума:

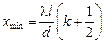 , (19.14)
, (19.14)
где k = 0, 1, 2, …
Расстояние между соседними минимумами называется шириной интерференционной полосы.
Найдем расстояние между (k + 1)-м и k-м минимумами:
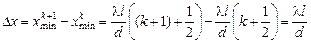 .
.
Запомним: ширина интерференционной полосы не зависит от порядкового номера полосы и равна
 . (19.15)
. (19.15)
СТОП! Решите самостоятельно: А9, А10, В8–В10, С10.
Билинза
Задача 19.6. Собирающая линза с фокусным расстоянием F = = 10 см разрезана пополам и половинки раздвинуты на расстояние h = 0,50 мм. Найти: 1) ширину интерференционных полос; 2) число интерференционных полос на экране, расположенном за линзой на расстоянии D = 60 см, если перед линзой имеется точечный источник монохроматического света с длиной волны l = 500 нм, удаленный от нее на расстояние а = 15 см.
| F = 10 см h = 0,50 мм D = 60 см l = 500 нм а = 15 см | Решение. 1. Прежде всего, выясним, почему линза, разрезанная на две половинки, дает интерференционную картину. Дело в том, что точечный источник S дает в каждой половинке по изображению S1 и S2 (рис. 19.24). Изображения эти действительные и являются когерентными источниками света, поскольку имеют общее происхождение – источник S. |
| Dх = ? N = ? |
Рис. 19.24 
Далее наша задача сводится к опыту Юнга, если мы сумеем найти расстояние d между источниками S1 и S2 и расстояние от источников до экрана l.
2. Сначала найдем расстояние b от линзы до изображений S1 и S2. Применим формулу линзы:
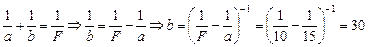 см.
см.
Тогда расстояние от источников до экрана:
l = D – b = 60 – 30 = 30 cм.
3. Найдем расстояние между источниками. Для этого рассмотрим подобные треугольники SO1O2 и SS1S2. Из их подобия следует
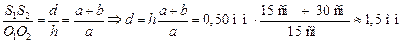 .
.
4. Теперь мы вполне можем воспользоваться формулой (19.15) и вычислить ширину интерференционной полосы:
 =
= 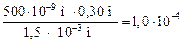 м = 0,10 мм.
м = 0,10 мм.
5. Чтобы определить, сколько интерференционных полос получится на экране, изобразим поле интерференции, т.е. ту область, в которой перекрываются волны от когерентных источников S1 и S2 (рис. 19.25).
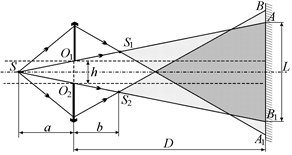 Рис. 19.25
Рис. 19.25
Как видно из рисунка, лучи от источника S1 покрывают область S1AA1, а лучи от источника S2 покрывают область S2ВВ1. Поле интерференции – область, которая является пересечением этих областей, показана более темной штриховкой. Размер интерференционной полосы на экране – это отрезок АВ1, обозначим его длину через L.
Рассмотрим треугольники SO1O2 и SAB1. Из их подобия следует
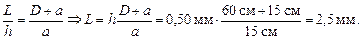
Если на участке длиной L содержатся N полос, длиной Dх каждая, то

Ответ: Dх = 0,10 мм; N = 25.
СТОП! Решите самостоятельно: D4, D5.
Дата добавления: 2016-04-11; просмотров: 5967;
