ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ СВЕТА
С волновой точки зрения свет представляет собой электромагнитные волны, т.е. процесс распространения колебаний связанных между собой электрического и магнитного полей. На рис. 1 изображена монохроматическая волна в непроводящей среде.
В отличие от упругих волн, электромагнитные волны могут распространяться в вакууме, при этом в каждой точке пространства в данный момент времени векторы напряженностей электрического 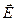 и магнитного и магнитного  полей перпендикулярны друг другу и перпендикулярны направлению распространения X. полей перпендикулярны друг другу и перпендикулярны направлению распространения X.
| 
|
| Рис.1 |
Скорость распространения света в вакууме С= 3 10см/с.
Вследствие однозначной связи между векторами 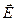 и
и  для описания происходящих процессов достаточно рассматривать один из векторов
для описания происходящих процессов достаточно рассматривать один из векторов 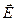 или
или  электромагнитной волны. Обычно это вектор
электромагнитной волны. Обычно это вектор 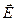 , так как действие света на вещество в большом числе случаев обусловлено электрической составляющей волны.
, так как действие света на вещество в большом числе случаев обусловлено электрической составляющей волны.
Допустим, что в какой-либо точке пространства происходит сложение двух волн одинаковой частоты w, а векторы 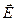 1 и
1 и 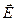 2 этих волн колеблются в одной плоскости:
2 этих волн колеблются в одной плоскости:
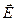 1
1 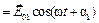 ,
,
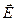 2
2 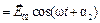 .
.
Модули векторов 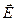 01 и
01 и 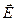 02 -- амплитуды этих колебаний, w - циклическая частота, a1 и a2 - начальные фазы колебаний.
02 -- амплитуды этих колебаний, w - циклическая частота, a1 и a2 - начальные фазы колебаний.
Согласно принципу суперпозиции напряженность результирующего поля 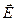 равна
равна
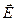 =
= 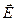 1 +
1 + 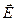 2 .
2 .
В эксперименте, как правило, регистрируется интенсивность световой волны - I, которая для плоской или сферической волн пропорциональна 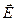 2. Можно показать, что:
2. Можно показать, что:
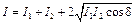 ,
,
где d = a1 - a2. Если разность фаз d взаимодействующих волн со временем не изменяется, то в тех точках, для которых cosd >0, интенсивность света превышает суммарную интенсивность I1 + I2 , а в точках, для которых cosd <0, она меньше I1 + I2. То есть в этом случае произойдет перераспределение светового потока в пространстве, в результате чего в одних местах возникнут максимумы освещенности, в других - минимумы.
Это явление называется ИНТЕРФЕРЕНЦИЕЙ. В общем случае интерференция волн заключается в пространственном перераспределении интенсивности результирующей волны в зависимости от поведения во времени амплитуд, фаз, частот, направлений поляризации интерферирующих волн. Необходимым условием существования устойчивой во времени интерференционной картины является согласованное протекание колебательных процессов в накладывающихся волнах. Для этого необходимо, чтобы эти волны были одинаковой частоты (w1= w2) и постоянной разности фаз (d =const). Такие волны называюткогерентными.
Наиболее отчетливо интерференция проявляется, когда две волны имеют одинаковую поляризацию, а их интенсивности равны I1 = I2, тогда в максимумах интенсивность света равна учетверенной исходной I= 4 I1, а в минимумах I=0.
В случае некогерентных волн, например, непрерывного изменения разности фаз d = a1 - a2, принимающей с равной вероятностью любые значения, среднее значение cosd будет равно нулю, а результирующая интенсивность I = I1 + I2, то есть интерференционный член 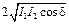 будет отсутствовать.
будет отсутствовать.
Когерентные волны можно получить, разделив (при помощи преломления или отражения) волну, излучаемую одним точечным источником. Если эти волны пройдут различные оптические пути, то при их последующем наложении будет наблюдаться интерференционная картина.
| Пусть разделение волны происходит в точке O, а встречаются волны в точке Р (рис.2.) Волна 1 проходит в среде с показателем преломления n1 путь S1, а волна 2 - в среде с n2 - путь S2, тогда разность фаз d колебаний волн 1 и 2 в точке Р: | 
|
| Рис.2 |
 ,
,
где n1 = С/V1, n2 = С/V2, V1 и V2 - скорости волн в первой и во второй среде соответственно, C - скорость света в вакууме.
Величина D = (n2S2 - n1S1 ) называется оптической разностью хода. Можно показать, что  , где l0 - длина волны света в вакууме, n- частота (2pn = w).
, где l0 - длина волны света в вакууме, n- частота (2pn = w).
Видно, что при D = ± ml, где m = 0,1,2,.., колебания в точке Р происходят с одинаковой фазой, т.е. наблюдается интерференционный максимум. Если D =(2m +1) l/2, то в точке Р наблюдается минимум.
Отклонение света от прямолинейного распространения в среде с резкими неоднородностями (например, у границ тел, у малых отверстий) называется ДИФРАКЦИЕЙ. Дифракция приводит к огибанию световыми волнами препятствий и частичному проникновению света в область геометрической тени. Для объяснения явления дифракции пользуются принципом Гюйгенса, в соответствии с которым, каждая точка волнового фронта является источником вторичных сферических волн, а результат их интерференции дает волновые поверхности в последующие моменты времени. В случае неограниченной волновой поверхности вторичные волны для любого направления (кроме прямолинейного) в результате интерференции гасят друг друга, так как для каждого элемента волновой поверхности DQ1 всегда найдется такой же по площади элемент DQ2, вторичная волна от которого по данному направлению отстает на l/2, то есть создает колебание, происходящее в противофазе по сравнению с колебанием от DQ1.
Если же волновая поверхность частично ограничена, то вторичные волны, излучаемые в определенных направлениях элементами открытого участка, не гасятся. Видно, что природа явлений интерференции и дифракции одинакова. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Исторически сложилось так, что перераспределение интенсивности, возникающее в результате суперпозиции волн, испускаемых конечным числом дискретных когерентных источников, принято называть интерференцией. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, испускаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией. Поэтому говорят, например, об интерференционной картине от двух узких щелей и о дифракционной картине от одной щели.
Различают два простейших вида дифракции. Дифракция в параллельных лучах, называемая дифракцией Фраунгофера, и дифракция сферических волн - дифракция Френеля.
Рассмотрим дифракцию Фраунгофера на узкой и длинной щели. На рис.3. щель расположена перпендикулярно плоскости чертежа.
Длина щели l значительно больше ее ширины b (l >>b). Пусть на щель падает плоская световая волна. За щелью находится собирающая линза, в фокальной плоскости которой располагается экран. Разобьем открытую часть волновой поверхности на зоны шириной dx. Вторичные волны, посылаемые зонами в направлении j, собираются в точке экрана Р.
Каждая элементарная зона создаст в точке Р элементарное колебание напряженности электрического поля dE. При фиксированном l амплитуда dA элементарного колебания пропорциональна dx (dA=c dx). Алгебраическая сумма А амплитуд колебаний, возбуждаемых всеми зонами в некоторой точке Р равна А= 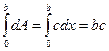 и, следовательно с=A/b, и dA= A/b dx.
и, следовательно с=A/b, и dA= A/b dx.
Разность фаз между колебаниями, создаваемыми отдельными зонами образуется на пути D =x sinj .
Если фазу колебания в зоне, находящейся в середине щели (x=0), принять равной нулю, то фаза колебания, создаваемого зоной с координатой x, равна:
d = 2pD/l = 2p x sinj /l.
Таким образом, в точке Р, положение которой на экране определяется углом j, элементарная зона с координатой j создает колебание, описываемое так:
 Результирующее колебание в точке Р, создаваемое всем открытым участком волновой поверхности, найдем, проинтегрировав dE по всей ширине щели. Результирующее колебание в точке Р, создаваемое всем открытым участком волновой поверхности, найдем, проинтегрировав dE по всей ширине щели.
|

|
| Рис.3 |
Получаем:
 (71.1) (71.1)
|
Выражение, стоящее в квадратных скобках, очевидно, равно амплитуде Аj результирующего колебания в точке Р (положение которой определяется углом j).
Так как интенсивность света I(j ) пропорциональна квадрату амплитуды, то:
 (71.2) (71.2)
|
Проанализируем полученные выражения. Амплитуда A(j) и интенсивность I(j ) обращаются в ноль когда,
sin 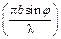 = 0,
= 0,
т. е. когда
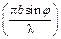 =± kp или bsinj = ± kl , (71.3) =± kp или bsinj = ± kl , (71.3)
|
здесь k - целое число.
Исключением является случай j= 0 (k=0), для этого угла
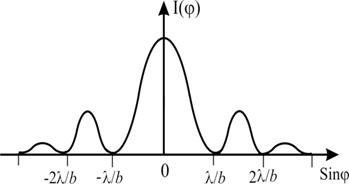
А(j )=А0 и I(j )=I0, так как lim(sinj /j) =1. Это значит, что в фокусе линзы наблюдается главный или "нулевой" максимум интенсивности. Распределение интенсивности на экране симметрично относительно центра I(j ) = I(-j ), принимает нулевые значения для тех точек, где выполняется условие bsinj= ±kl, в промежутках между нулевыми значениями I(j) наблюдаются максимумы интенсивности, убывающие по своей величине с удалением от центра (рис.4).
Положение максимумов с достаточной точностью определяется условием bsinj= ±(2k+1) l/2, число k называют порядком максимума. Подставив в выражение (71.2) значение sinj для k=1, 2, 3, и т. д., можно рассчитать относительные значения интенсивностей в различных порядках:
I1 : I2 : I3 = 1 :(2p/3)2 : :(2p/5)2 = 1: 0,045: 0,016.
Выражение bsinj представляет собой разность хода лучей в направлении j от крайних точек щели. Если эта разность равна целому числу длин волн, то в этом направлении будут распространяться колебания с полным набором фаз от 0 до 2p.
|
| Рис.4 |
Для любой зоны всегда найдется зона, создающая колебания в противофазе, и они будут гасить друг друга. Следовательно, интенсивность в точках, определяемых условием (71.3), действительно должна быть равна нулю.
Следует отметить, что sinj = ±kl/b не может быть больше единицы и, следовательно, kl < b, значит при b < l дифракционной картины не возникает. В этом случае освещенность на экране монотонно уменьшается от середины к краям.
Для очень широкой щели (b >> l) на экране наблюдается яркое и четкое изображение источника света, образуемое по законам геометрической оптики.
ДИФРАКЦИОННАЯ РЕШЕТКА - это оптическое устройство, представляющее собой совокупность большого числа регулярно расположенных штрихов (канавок, щелей, выступов), нанесенных на плоскую или вогнутую оптическую поверхность. Бывают прозрачные и отражательные дифракционные решетки. В зависимости от профиля штриха они могут концентрировать излучение в определенном направлении. Расстояние между соответствующими точками соседних щелей называется периодом решетки d.
Рассмотрим прозрачную дифракционную решетку. Расположим за решеткой собирающую линзу (рис.5).

|
| Рис.5 |
При падении плоской волны на систему параллельных щелей пучки света, расходящиеся вследствие дифракции, когерентны между собой и интерферируют, образуя в фокальной плоскости линзы распределение освещенности с резкими максимумами. В промежутках между этими "главными" максимумами образуется N - 1 добавочных минимумов и N - 2 максимумов, где N - число щелей.
Как видно из рисунка, угол, определяющий положение главных максимумов в фокальной плоскости линзы, определяется из условия интерференционного усиления вторичных волн от соседних щелей. Разность хода должна быть равна целому числу длин волн
| d sinj = kl, k= 0, 1, 2, ... (71.4) |
В отличие от образуемой одной щелью дифракционной картины с широкими дифракционными максимумами, в случае дифракционной решетки на экране наблюдаются узкие интенсивные максимумы освещенности, ширина которых много меньше расстояний между ними.
Этот эффект легко понять из энергетических соображений: при увеличении числа интерферирующих пучков в N раз общий световой поток также возрастает в N раз, но интенсивность в максимумах возрастает в N2 раз, что возможно только при условии, что их ширина одновременно уменьшается в N раз.
Положение максимумов (кроме центрального с k = 0) зависит от длины волны l. Поэтому дифракционная решетка может служить диспергирующим элементом спектрального прибора, предназначенного для пространственного разложения исследуемого немонохроматического электромагнитного излучения в спектр.
| <== предыдущая лекция | | | следующая лекция ==> |
| Іонні основи генерації ПД | | | ТЕПЛОПРОВОДНОСТЬ ТВЕРДЫХ ТЕЛ. |
Дата добавления: 2016-04-19; просмотров: 1358;
