Интерференция от двух когерентных источников

Рассчитаем интерференционную картину от двух когерентных источников (например, от двух щелей Юнга), расположенных достаточно близко друг от друга. Пусть щели S₁ и S₂ находятся на расстоянии d друг от друга (см. рис. 2.8). Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l , причем l >> d. Пусть начало отсчета находится в точке О, симметричной относительно щелей.

Интенсивность в любой точке А экрана, лежащей на расстоянии x от О, определяется оптической разностью хода Δ = r₂n₂ - r₁n₁. Это следует из рассмотрения сложения световых волн, излучаемых источниками S₁ и S₂.

Источник S₁ излучает световую волну:

Аналогично источник S₂ излучает световую волну:

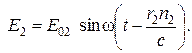
Рис. 2.8

Сложение этих двух волн при условии E₀₁ = E₀₂дает следующий результат:

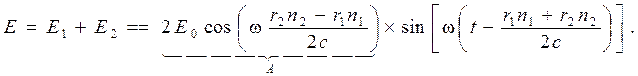
Тогда интенсивность света I, пропорциональная квадрату амплитуды A (I ~ A²), будет равна

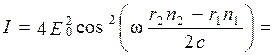
Здесь учтено, что

и, как указывалось выше, величина

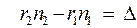
есть оптическая разность хода.

Т. к. результирующая интенсивность пропорциональна квадрату косинуса, то возможны два случая ее существования:

Следовательно,

условие интерференционных min: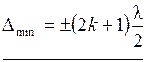

и условие интерференционныхmax:

Здесь k = 0,1,2…– порядок интерференционного максимума.

Определим положение максимумов интерференционной картины на экране. Сначала найдем

.

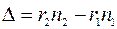Полагая n₂ = n₁ = 1, найдем разность (r₂ – r₁). Из вышеприведенного рисунка 2.8 следует:

.

Отсюда

Следовательно, положение максимумов на экране определяется при:

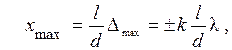
а положение минимумов при:

Здесь, по-прежнему, k = 0,1,2… .

Тогда ширина интерференционной полосы (т.е. расстояние между двумя соседними максимумами) будет:

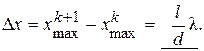
Таким образом, ширина интерференционной полосы будет зависеть от длины волны λ .