Интерференция света в тонких пленках
Рассмотрим ход лучей в плоскопараллельной пластинке (рис. 2.9).
Из рисунка 2.9 следует, что оптическая разность хода Δ двух лучей 1′ и 2 (c учетом того, что луч 1′ отражается от более плотной среды и теряет половину длины волны) будет равна:
 |
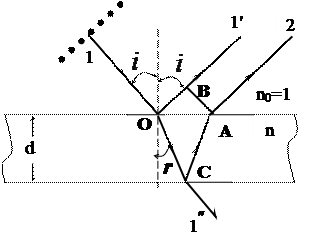Рис. 2.9
.
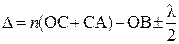Здесь член ±λ/2 обусловлен потерей полуволны при отражении света от границы раздела. Если n > n0, то потеря полуволны произойдет в точке О и указанный член λ/2 будет иметь знак минус; если же n < n0 , то потеря полуволны произойдет в точке С и λ/2 будет иметь знак плюс.
Если учесть закон преломления света
,
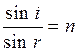то геометрические преобразования дадут
.
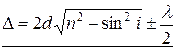В рассматриваемом типе интерференции возникают:
а) полосы равного наклона (i = const);
б) полосы равной толщины (d = const);
в) кольца Ньютона (rk).
В случае плоскопараллельной пластинки (пленки) интерференционная картина определяется величинами l, d, n, i. Для данных l, d, n каждому углу наклона соответствует своя интерференционная полоса.
Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона(см. вышеприведенный рисунок).
Так как лучи 1′ и 2 параллельны, то для наблюдения интерференции нужна собирающая линза и экран, расположенный в фокальной плоскости линзы. В частности, если оптическая ось линзы перпендикулярна поверхности пластины, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
Если пластинка имеет форму клина с очень малым углом между гранями, то оптическая разность хода интерферирующих параллельных лучей 1′ и 2 уже определяется толщиной d. Каждая из полос интерференции при этом возникает от мест пластинки, имеющих одинаковую толщину. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины.В отраженном от клина нормально падающем свете наблюдаются интерференционные полосы, параллельные ребру клина.
Классическим примером полос равной толщины являются кольца Ньютона, которые наблюдаются при отражении (или прохождении) света в области воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 2.10).
R R
|
Рис. 2.10
В отраженном свете оптическая разность хода (с учетом одного отражения от более плотной среды и показателя преломления воздуха n = 1) равна:
D = 2d +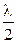 
.
Из геометрии (рис. 2.10) следует, что R2 = (R – d)2 + r2 , где R – радиус кривизны линзы, r – радиус окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d очень мало, можно записать:
d =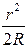 
.
Следовательно,
D =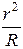 
+ 
.
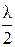Приравнивая это выражение к условиям максимума и минимума, получим выражения для радиуса m-го светлого кольца:
rm =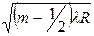 
(m = 1,2,3,…)
и радиуса m-го темного кольца:
rm =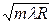 
(m = 0,1,2,3,…).
При наблюдении интерференции в проходящем свете и нахождении радиусов колец нужно учитывать, что 2-й луч испытывает при прохождении два отражения от более плотной среды, то есть разность хода лучей будет иметь вид:
D = 2d + 2 .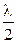
При этом условия максимума и минимума поменяются местами: максимумы интерференции в отраженном свете соответствуют минимумам интерференции в проходящем свете и наоборот (см. табл. 3).
Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны λ. Поэтому системы светлых и темных полос получается только в монохроматическом свете. При наблюдении же в белом свете получается система цветных (радужных) полос.
Таблица 3
| Радиус светлого кольца | Радиус темного кольца | |
| В отраженном свете | rm =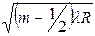 
| rm =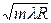 
|
| В проходящем свете | rm =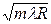 
| rm =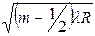
|
Интерферометры
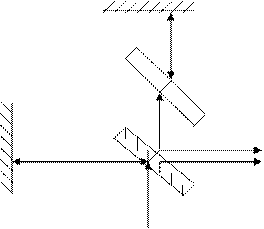
Интерференция света широко используется в приборах, называемых интерферометрами. Интерферометр– это очень чувствительныйоптический измерительный прибор, принцип действия которого основан на явлении смещения интерференционной картины (например, в интерферометре Майкельсона 1).
В этом интерферометре (см. рис. 2.11) луч света от источника разделяется на два когерентных луча с помощью полупрозрачного зеркала.
[1] А. Майкельсон (1852–1913), американский физик.
1/
2/
* S
|
Рис. 2.11
Лучи 1/ и 2/ когерентны. Поэтому будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 и луча 2. При перемещении одного из зеркал на расстояние l/4 разность хода обоих лучей изменится на l/2 и произойдет смена освещенности зрительного поля. Тогда по незначительному смещению интерференционной картины можно судить о перемещении одного из зеркал и использовать интерферометр Майкельсона для достаточно точных (до 10-9м) измерений длины (измерения длины тел, длины световой волны и др.)
Одновременно, интерферометр –очень чувствительныйоптический прибор, позволяющий определять незначительные изменения показателя преломления прозрачных тел (газов, жидкостей, твердых тел) в зависимости от давления, температуры, примесей и т.д. Такие интерферометры получили название интерференционных рефрактометров.
На пути интерферирующих лучей располагаются две одинаковые кюветы длиной L, одна из которых заполнена, например, газом с известным n0, а другая – с неизвестным (nx) показателями преломления. Возникающая между ними дополнительная оптическая разность хода D = (nx – n0)l. Изменение разности хода приведет к сдвигу интерференционных полос:
m0 = D/l = (nx – n0)l/l,
где m0 показывает, на какую часть ширины интерференционной полосы сместилась интерференционная картина. Измеряя величину m0 при известных l, n0 и l можно вычислить nx с очень большой точностью.
Дата добавления: 2016-04-22; просмотров: 1128;