Занятие 7. Интерференция света

Задача 10.1

На ДФ диафрагму с узкой S щелью падает в вакууме монохроматическая световая волна, за которым расположено бизеркало Френеля. Угол α между зеркаламиФренеля равен12' , т.е. α = 12' , расстояние от линии пересечения зеркал, на которой находится O точка, до этой узкой S щели и

Э экрана равны соответственно r = 10,0 см и b = 130 см. Длина волны света в вакууме монохроматической световой волны λ₀ = 0,55 мкм.

Определить:а) ширину Δz_ш интерференционнойполосы на Э экране и m числовозможных интерференционныхмаксимумов, возникающих на этом Э экране;

б) сдвигΔzинтерференционнойкартины на Э экране при смещении S щелипо дуге окружности с центром в O точке и r = 10,0 см радиусом на длину этой дуги, равной δl = 1,0 мм;

в) при какой максимальнойh_max ширине S щели интерференционныеполосы на Э экране будут наблюдаться достаточно отчётливо?

изображения S щели соответственно в З' и З'' зеркалах. Эти S' и S'' мнимые изображения S щели находятся на окружности с центром в O точке и r радиусом. Перпендикуляры (рис. 10.1) n₁ и n₂, опущенные из S щели соответственно на продолжение плоскости З' зеркалаи плоскость З'' зеркалаи используемые для построения S' и S'' мнимых изображений S щели, пересекаются в S щели под α углом, равным α углу между зеркаламиФренеля. ЩельS и два её S' и S'' мнимых изображений находятся на окружности с центром в O точке и

(рис. 10.1) r радиусом, поэтому n₁ и n₂ перпендикуляры, пересекающиеся в S щели под α углом, являются внутреннимуглом в этой окружности с центром в O точке и r радиусом и опираетсяна

S' S'' дугу. На ту же S' S''дугу опирается центральныйугол, образованный продолжением

1' и 1'' отражённых световых лучей. Поэтому угол между отражёнными 1' и 1'' световыми лучамиравен 2α.

Простым построением отражённых лучей от З' и З'' зеркал, которые вызваны падающим световым лучомот Sщели в направлении, отличнымот направления светового (рис. 10.1) 1 луча, можно доказать, что все эти отражённых лучи от З' и З'' зеркал будут попадать на Э экран в его области z_ш шириной. Вследствие малости α угламежду зеркаламиФренеляz_ш ширина области, в которую попадают все отражённые лучи от З' и З'' зеркал, имеет следующий вид: z_ш = 2bα. (1.1) где b - расстояние от линии пересечения З' и З'' зеркал, на которой находится O точка, до Э экрана.

S' и S'' мнимыми изображениями в З' и З'' зеркалах, вследствие чего для анализа интерференционнойкартины на Э экране (рис. 10.1) в его области z_ш шириной возможно применить схему от двух

S₁ и S₂ источников (рис. 10.4) из раздела 10.1 "Электромагнитная природа света. Интерференция света".

Согласно (10.44) из раздела 10.1 "Электромагнитная природа света. Интерференция света" Δz_шширинаинтерференционныхполос с учётом расстояния до Э экрана, равного примерно b + r, от двух источниковкогерентныхотражённых световыхволн, которыми на рис. 10.1 являются S' и S'' мнимые изображения в З' и З'' зеркалах, имеет следующий вид: Δz_ш ≈ (b + r)λ₀/h.(1.3) Подставляем (1.2) d расстояниемежду S' и S'' мнимыми изображениями S щели в

З' и З'' зеркалах в (1.3) и получаем следующее окончательное выражение Δz_ш шириныинтерференционныхполос на Э экране (рис. 10.1) в его области z_ш шириной:

Δz_ш ≈ (b + r)λ₀/2rα ≈ 1,1 мм.(1.4) Число m возможных интерференционныхмаксимумов, возникающих на Э экране в его области z_ш шириной с учётом (рис. 10.4) из раздела 10.1 "Электромагнитная природа света. Интерференция света" интерференционного максимумав центре Э экрана 0 max, т.е. нулевого порядка, а также с учётомокругления полученного m числа с его уменьшением до ближайшего целого значения это m число возможных интерференционныхмаксимумов имеет следующий вид:

m = (z_ш/Δz_ш) + 1 = {4brα²/[(b + r)λ₀]} + 1 ≈ 9.(1.5) где (1.1) z_ш = 2bα - ширина области, в которую попадают все отражённые лучи от З' и З'' зеркал; Δz_ш ≈ (b + r)λ/2rα - ширина(1.4)интерференционныхполос на Э экране (рис. 10.1.1.1) в его области

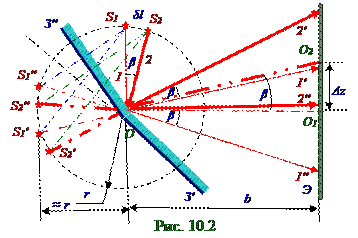
При смещении S щелипо дуге окружности с центром в O точке и r радиусомна центральныйβ угол из (рис. 10.2) S₁ положения в S₂ положение на такой же β угол смещаются отражённые от З' и З'' зеркал 2' и 2''световые лучи соответственноотносительно отражённых от этих З' и З'' зеркал 1' и 1''световыхлучей соответственно, когда S щельнаходится в S₁ положении.

На такой же (рис. 10.2) β угол смещается OO₂ линия, делящая пополамугол между отражёнными от З' и З'' зеркал 2' и 2''световые лучами соответственно, относительно OO₁ линии, делящей пополамугол между отражёнными от З' и З'' зеркал 1' и 1''световымилучами соответственно. Пересечения этих OO₁, OO₂ линий с плоскостью Э экрана определяют положения центра интерференционнойкартины. Поэтому Δzлинейноесмещение (рис. 10.2) центра интерференционнойкартины при смещении S щели по дуге окружности с центром в O точке и

r радиусом на центральныйβ уголиз S₁ положения в S₂ положение с учётом малостиэтого центрального β угла, а также с учётом b расстояния до Э экрана от линии пересечения З' и З'' зеркал, на которой находится O точка, имеет следующий вид: Δz ≈ bβ. (1.7) Подставляем (1.6) в (1.7) и получаем следующее Δzлинейноесмещение (рис. 10.1.1.2) центра интерференционнойкартины на Э экране при смещении S щелипо дуге окружности с центром в

O точке и r радиусом на длину этой дуги, равной δl: Δz ≈ bδl/r =13 мм. (1.8) При расширении S щелив ДФ диафрагме(рис. 10.1) до значения h леваяи праваяграницы этой S щелисогласно принципу Гюйгенса- Френеля(рис. 10.15) из раздела 10.1 "Электромагнитная природа света. Интерференция света" является источником вторичной сферической волны, т.е. при расширении S щелив ДФ диафрагмедо h значения образуются дваисточника вторичной сферической волны. Каждый из этих двухисточников вторичной сферической волны образует на Э экране своюинтерференционнуюкартину, центры которых имеют Δzлинейноесмещение, рассчитываемое по (1.8), где вместо смещения S щелипо дуге окружности с центром в O точке и r радиусом на длину этой дуги, равной δl, используется h ширина этой S щелив ДФ диафрагме, вследствие чего выражение для расчёта Δzлинейногосмещения принимает следующий вид: Δz ≈ bh/r. (1.9)

Если (1.9) Δzлинейноесмещение между (рис. 10.47) из раздела 10.2 " Дифракция света" интерференционнымимаксимумами от каждого из двухисточников вторичной сферической волны, которые возникают при расширении S щелив ДФ диафрагмедо h значения, будет не большеполовины Δz_ш ширины(1.4)интерференционныхполос на Э экране, рассчитанной при условии (рис. 10.1) узкой S щелив ДФ диафрагме, то интерференционныеполосы на Э экране будут наблюдаться достаточно отчётливо, поэтому условиеотчётливогонаблюдения интерференционныхполос на Э экране имеет следующий вид: Δz ≤ Δz_ш/2. (1.10)

МаксимальноеΔz_max значение линейногосмещения между интерференционнымимаксимуми, которое согласно (1.9) получается при ширине S щелив ДФ диафрагме,равной h_max,будет при замененеравенства (1.10) следующим равенством: Δz_max = Δz_ш/2. (1.11) Подставляем в (1.11) выражение (1.9), связывающее Δz величинулинейногосмещения между интерференционнымимаксимуми от каждого из двухисточников вторичной сферической волны с шириной S щелив ДФ диафрагме,равной h, а также подставляем выражение в (1.11) выражение (1.4) ширины Δz_ш интерференционныхполос на Э экране, в результате чего получаем следующее выражение, определяющее максимальноеh_max значение ширины S щелив ДФ диафрагме, до которой можно расширять величину щели без нарушения отчётливогоизображения интерференционныхполос на Э экране: bh_max /r = (b + r)λ₀/4rα ↔ h_max = [1 + (r/b)]λ₀/4α ≈ 43 мкм. (1.12)

Задача 10.2

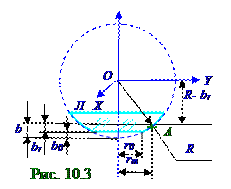
r₀ радиуса уменьшается по сравнению с 2b оптическим(10.67) из раздела 10.1 "Электромагнитная природа света. Интерференция света" ходом1′′ световоголуча, отражённого от верхнейповерхностиПл.2 прозрачнойпластины, в случае (рис. 10.11) из раздела 10.1 "Электромагнитная природа света. Интерференция света" использования несошлифованной плоско - выпуклойЛ линзы, на величину, равную удвоенной толщине (2.1) 2b₀ сошлифованного участка r₀ радиуса, и этот оптический 2b_r ход1′′ световоголуча имеет следующий вид:

2b_r = 2b - 2b₀ ↔ 2b_r = (r_m ^{2 -} r₀ ²)/R. (2.2) Подставляем (2.2) в (10.67) из раздела 10.1 "Электромагнитная природа света. Интерференция света" и получаем (рис. 10.10) из раздела 10.1 "Электромагнитная природа света. Интерференция света" следующую оптическую Δ_с разность ходамежду 1′ световымлучом, отражённым от нижнейповерхности Л линзы, и 1′′ световымлучом, отражённым от верхнейПл.2 поверхностипрозрачнойпластины, в случае (рис. 10.3) использования плоско - выпуклойЛ линзы с сошлифованным участком r₀ радиуса: Δ_с = 2b_r + (λ₀/2) = [(r_m ^{2 -} r₀ ²)/R] + (λ₀/2). (2.3) Подставляем (2.3) в (10.70) из раздела 10.1 "Электромагнитная природа света. Интерференция света" и получаем следующее условие интерференционных максимумови минимумовмежду когерентными световыми(рис. 10.10) из раздела 10.1 "Электромагнитная природа света. Интерференция света" 1′ и 1′′ лучами, отражёнными соответственно от нижнейповерхности Л линзы и от верхнейПл.2 поверхностипрозрачнойпластиныс тем различием, что в данной задаче используется плоско - выпуклая Ллинза с сошлифованным участком r₀ радиуса: [(r_m ^{2 -} r₀ ²)/R] + (λ₀/2) = mλ₀/2. (2.4) Решаем (2.4) относительно r_m радиусовинтерференционных светлых колец, где m = 1, 3, 5, …, и r_m радиусовинтерференционных тёмных колец, где m = 0, 2, 4, 6,…, и получаем следующее выражение для их значений для данной задачи, в которой используется плоско - выпуклаяЛ линзас сошлифованным участком r₀ радиуса: r_m = [r₀ ² +(Rλ₀m/2)]^1/2. (2.5)Согласно (рис. 10.10) из раздела 10.1 "Электромагнитная природа света. Интерференция света" шестой интерференционныймаксимум, т.е. шестоесветлое кольцо, имеет порядковый номер со следующим значением: m = 11.(2.6)Подставляем порядковый (2.6) номер m = 11 в выражение (2.5) и получаем следующее значение радиусашестогосветлого кольцаНьютона для данной задачи, в которой используется плоско - выпуклая Ллинзас сошлифованным участком r₀ радиуса: r_m ≈ 3,8 мм.(2.7)

Задача 10.3

Линзу диаметром D = 5, 0 см и с фокусным расстоянием f = 25, 0 см разрезали по диаметру на две одинаковые половины, причём удалённым оказался слой толщины a = 1, 00 мм. После этого обе половины сдвинули до соприкосновения и в фокусе полученной таким образом билинзы Бийепоместили параллельно разрезу узкую щель, испускающую монохроматический свет в вакууме с λ₀ = 0, 64 мкм длиной волны. За билинзой Бийерасположили экран на расстоянии b = 50, 0 см от неё. Определить:

а) ширину Δz_шинтерференционнойполосы наэкранеи число m возможных максимумов;

б) ширину щели h_max, при которой полосы на экране будут наблюдаться ещё достаточно отчётливо.

оптической осью зелёной Л полулинзы равно a толщине удалённого слоя.

Световаяволны в вакууме от S источника является цилиндрической, т.е. плоскости равных фазэтой световойволны являются окружностис центром в S точке расположения источника. Поэтому на площади полулинз падающие лучи имеют в данном направлении одинаковый угол падения.

Световой луч, нормальный (рис. 10.4) площади полулинз и падающий на стык этих полулинз, вследствие преломления в каждой из полулинз, раздваивается. После преломления в синей Л полулинзе световой луч пересекает ГО главную оптическую ось синей Л полулинзыв F фокусе, а после преломления в зелёной Л полулинзе световой луч пересекает ГО главную оптическую ось зелёной Л полулинзыв F фокусе.

Световые лучи, падающие (рис. 10.4) на площадь полулинз под φ_max максимальными углами падения, вследствие преломления направляются в точки пересечения ПО побочной оптическую оси синей Л полулинзы и ПО побочной оптическую оси зелёной Л полулинзы с ФП фокальной плоскостью этих полулинз.

Световой луч, нормальный (рис. 10.4) площади полулинз и падающий на стык этих полулинз, вследствие преломления в каждой из полулинз, раздваивается, вследствие чего образуется область когерентных световыхволн, ограниченная световымиволнами, имеющими α угол между направлениями распространения.

Угол α между направлениями распространения раздвоенных световыхволн с учётом его малого значения имеет (рис. 10.4) следующее значение: α ≈ a/f, (3.1)

где a - толщина удалённого слоя линзы, разрезанной по диаметру на две одинаковые половины;

f - фокусное расстояние каждой из полулинз.

Согласно (10.44) из раздела 10.1 "Электромагнитная природа света. Интерференция света" Δz_шширинаинтерференционныхполос от когерентных плоских световых волн, распространяющихся под α углом друг к другу, имеет следующий вид: Δz_ш ≈ λ₀/α, (3.2)

где α ≈ d/(b + r) - угол (рис. 10.4) из раздела 10.1 "Электромагнитная природа света. Интерференция света", под которым когерентные плоские световые волны распространяются к Э экрану.

Подставляем (3.1) в (3.2) и получаем для монохроматического света в вакууме с заданной λ₀ длиной волны следующее выражение Δz_ш ширины интерференционныхполос на Э экране, зависящее от a толщины удалённого слоя линзы, f фокусного расстояния каждой из полулинз и не зависящее от bрасстояниябилинзы Бийе до Э экрана: Δz_ш ≈ λ₀ f/a ≈ 0, 16 мм. (3.3)

Согласно (рис. 10.4)ширина z_ш зоны интерференции с учётом (3.1) величины α угла, под которым когерентные плоские световые волны распространяются к Э экрану, и с учётом величины

bрасстояниябилинзы Бийе до Э экрана имеет следующее значение: z_ш ≈ bα = ba/f. (3.4)

Отношение(3.4)ширины z_ш зоны интерференциик (3.3) ширине Δz_ш интерференционныхполос от когерентных плоских световых волн определяют с учётом (рис. 10.4) из раздела 10.1 "Волновые свойства света" интерференционного максимумав центре Э экрана 0 max, т.е. нулевого порядка, а также с учётомокругления полученного m числа с его уменьшением до ближайшего целого значения, вследствие чего это m число возможных интерференционныхмаксимумов имеет следующий вид: m = (z_ш/Δz_ш) + 1= (ba² /λ₀ f ²)+ 1 ≈ 13. (3.5)

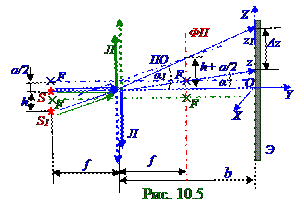
направляется в точку пересечения ПО побочной оптическую оси синей Л полулинзы с ФП фокальной плоскостью этой полулинзы. Точка пересечения ПО побочной оптическую оси синей Л полулинзы с ФП фокальной плоскостью находится на h+ a/2 расстоянии от OY оси, проходящей через стык полулинз и S источник, поэтому α₁ угол, под которым распространяется один из раздвоенных лучей после преломления в синей Л полулинзе, имеет следующее значение: α₁ ≈ (h+ a/2)/f. (3.6)

Согласно (рис. 10.5)верхняя z₁ координата зоны интерференции при расширении щелипо

OZ оси до h величиныс учётом (3.6) величины α₁ угла, под которым когерентные плоские световые волны распространяются к Э экрану, и с учётом величины bрасстояниябилинзы Бийе до Э экрана имеет следующее значение: z₁ ≈ bα₁ = b(h+ a/2)/f. (3.7)

Смещение Δz верхней z₁ координаты зоны интерференции(рис. 10.1.1.5) при расширении щелипо OZ оси до h величины относительно верхней z координаты зоны интерференциипри наличии только узкой щели, т.е. при наличии только S источника, имеет с учётом (3.4), (3.7) следующее значение: Δz = z₁ - z = [b(h+ a/2)/f] - (ba/2f) = bh/f.(3.8)

Смещение Δz верхней z₁ координаты зоны интерференции(рис. 10.5) при расширении щелипо OZ оси до h величины приводит к расширению ширины интерференционныхполос на эту

Δz величину. Поэтому интерференционныеполосы от узкой щели, т.е. при наличии только

S источника, накладываются на интерференционныеполосы от щели h величины, т.е. при наличии

S₁ источника.

Согласнокритерию Релея (рис. 10.47) из раздела 10.2 "Волновые свойства света" интерференционныеполосы при их наложении от двух источников, т.е. (рис. 10.5) от

S, S₁ источников, будут различимы, если (3.3) Δz_ш/2 полуширина интерференционныхполос на

Э экране будет не больше(3.8) смещения Δz верхней z₁ координаты зоны интерференции при расширении щелипо OZ оси до h величины относительно верхней z координаты зоны интерференциипри наличии толькоузкой щели,т.е. эти интерференционныеполосы будут различимы, если выполняется следующее неравенство: Δz ≤ Δz_ш/2 ↔ bh/f ≤ λ₀ f/2a. (3.9)

Согласно (3.9) h_max максимальноезначение (рис. 10.5)ширины щелипо OZ оси, при которой интерференционныеполосы будут различимы, определится из следующего равенства:

h_max = λ₀ f ²/2ba = 40 мкм. (3.10)

Задача 10.4

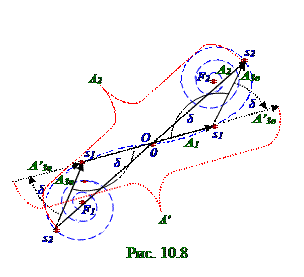
Результирующая A₁ амплитуда вектора A₁ плоской световой волны на Э экране (рис. 10.7) посередине геометрической тени Щ₁ щели, т.е. в M точке на Э экране, с величиной d = b₁/2 полуширины в непрозрачной Пл плоскости, определится (рис. 10.32) из раздела 10.2 "Электромагнитная природа света. Интерференция света" на спирали Корню длиной вектора A₁, направленного из точки с s₁ = 0_, 6 параметром в левойчастиспирали Корню в точку с s₁ = 0_, 6 параметром в правойчастиспирали Корню, где величина s₁ = 0_, 6 параметра спирали Корню определяется (10.114) из раздела 10.2 "Электромагнитная природа света. Интерференция света" следующим (рис. 10.8) соотношением: s₁ = (b₁/2) (2/lλ₀)^1/2 ≈ 0_, 6. (4.1)

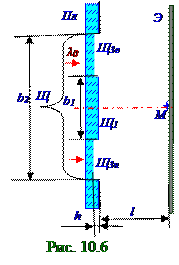
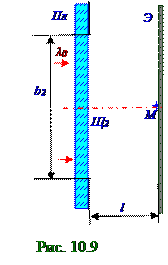
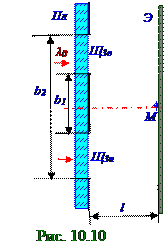
Результирующая A₂ амплитуда вектора A₂ плоской световой волны на Э экране (рис. 10.9) посередине геометрической тени Щ₁ щели, т.е. в M точке на Э экране, с величиной d = b₂/2 полуширины в непрозрачной Пл плоскости, определится (рис. 10.32) из раздела 10.1 "Электромагнитная природа света. Интерференция света" на спирали Корню длиной вектора A₂, направленного из точки с s₂ = 1_, 1 параметром в левойчастиспирали Корню в точку с s₂ = 1_, 1 параметром в правойчастиспирали Корню, где величина s₁ = 1_, 1 параметра спирали Корню определяется (10.114) из раздела 10.2 "Электромагнитная природа света. Интерференция света" следующим (рис. 10.8) соотношением: s₂ = (b₂/2) (2/lλ₀)^1/2 ≈ 1_, 1. (4.2)Результирующая A_3н амплитуда вектора A_3н плоской световой волны в M точке на Э экране (рис. 10.10) от нижнейЩ_3н щели b₂ - b₁ шириной при отсутствии выемки(рис. 10.6) h глубиной

в стеклянной Пл пластине, определится (рис. 10.32) из раздела 10.1 "Электромагнитная природа света. Интерференция света" на спирали Корню длиной вектора A_3н, направленного (рис. 10.8) из точки с s₂ = 1_, 1 параметром в левойчастиспирали Корню в точку с s₁ = 0_, 6 параметром в этой же левойчастиспирали Корню.

Результирующая A_3в амплитуда вектора A_3в плоской световой волны на Э экране (рис. 10.10) от верхнейЩ_3в щели b₂ - b₁ шириной при отсутствиивыемки(рис. 10.1.6) h глубиной в стеклянной Пл пластине, определится (рис. 10.32) из раздела 10.1 "Волновые свойства света" на спирали Корню длиной вектора A_3в, направленного (рис. 10.8) из точки с s₁ = 0_, 6 параметром в правойчастиспирали Корню в точку с s₂ = 1_, 1 параметром в этой же правойчастиспирали Корню.

Согласно (рис.10.8)результирующий вектор A₂ с A₂ амплитудой плоской световой волны от Щ₂ щели (рис.10.9) с величиной d = b₂/2 полуширины в непрозрачной Пл плоскостиполучаетсясуммой A₁ результирующеговектора плоской световой волны от Щ₁ щели (рис. 10.7) с величиной

верхнейЩ_3н, Щ_3в щелей (рис. 10.6) при наличии выемкиh глубиной в стеклянной Пл пластине, равные по величине амплитудам двух A_3н, A_3в результирующихвекторов плоской световой волны в M точке на Э экране от соответственно нижней,верхнейЩ_3н, Щ_3в щелей (рис. 10.10) при отсутствии выемки(рис. 10.6) h глубиной в стеклянной Пл пластине.

Согласно (рис. 10.8) суммарнаяA′результирующая амплитуда A′ вектора плоской световой волны в M точке на Э экране в случае сонаправленности двух A′_3н, A′_3в результирующихвекторов плоской световой волны отнижней,верхнейЩ_3н, Щ_3в щелей A₁ результирующемувектору плоской световой волны от Щ₁ щели (рис. 10.7) больше суммарной результирующейA₂ амплитуды вектора A₂ плоской световой волны в случае, когда два A_3н, A_3в результирующихвекторов плоской световой волны отнижней,верхнейЩ_3н, Щ_3в щелей (рис. 10.10) составляют δ угол с A₁ результирующимвектором плоской световой волны от Щ₁ щели. Для поворота (рис. 10.8) по "часовой стрелке" двух A_3н, A_3в результирующихвекторов плоской световой волны от соответственно нижней,верхнейЩ_3н, Щ_3в щелей (рис. 10.10) на δ угол, равный примерноπ/2, т.е. δ ≈ π/2, до положения, когда векторы A′_3н, A′_3в становятся сонаправленными A₁ результирующему вектору плоской световой волны от Щ₁ щели

nпоказателем преломлениягеометрический путь,равный h глубине выемки в стеклянной пластине. ОптическаяΔразность хода(10.32) из раздела 10.1 "Электромагнитная природа света. Интерференция света" между оптическимпутём(рис. 10.1.6) плоской световой волны от нижней,верхнейЩ_3н, Щ_3в и Щ₁ щелей имеет с учётом (4.4) следующий вид: Δ = l_o - l_o ′ = h(n - 1). (4.5) Разность Ф₃ - Ф₁ фаз плоской световой волны от нижней,верхнейЩ_3н, Щ_3в и Щ₁ щелей, т.е.

δ угол (рис. 10.8) между A_3н, A_3в результирующимивекторами плоской световой волны от соответственно нижней,верхнейЩ_3н, Щ_3в щелей и A₁ результирующимвектором плоской световой волны от Щ₁ щели равен примерноπ/2, т.е. δ ≈ π/2, при отсутствии выемки(рис. 10.6) h глубиной в стеклянной Пл пластине.

Для поворота (рис. 10.8) по "часовой стрелке" двух A_3н, A_3в результирующихвекторов плоской световой волны от соответственно нижней,верхнейЩ_3н, Щ_3в щелей (рис. 10.10) на δ угол, равный примерноπ/2, т.е. δ ≈ π/2, до положения, когда векторы A′_3н, A′_3в становятся сонаправленными A₁ результирующему вектору плоской световой волны от Щ₁ щели (рис. 10.7) нужно в этих нижней,верхнейЩ_3н, Щ_3в щелях (10.32) из раздела 10.1 "Электромагнитная природа света. Интерференция света"сделать выемку(рис. 10.6) с учётом (4.5) следующей h_min глубиной:

δ = (2π/λ₀ )Δ ↔ δ = (2π/λ₀ )h_min (n - 1) ↔ π/2 = (2π/λ₀ )h_min (n - 1) ↔ h_min = λ₀/4(n - 1). (4.6)

При выполнении (рис. 10.6) выемки(4.6) h_min глубиной плоские световые волны будут приходить в одной Ф фазе от нижней,верхнейЩ_3н, Щ_3в щелей и от Щ₁ щели стеклянной Пл пластины, поэтому в M точке на Э экране освещённость будет максимальной.