Можно ли увидеть изображение на экране?

Читатель: Допустим, перед собирающей линзой находится небольшой источ­ник света, например, зажженная свеча, а за линзой – непрозрачный эк­ран (рис. 7.26). Возникает вопрос: увидим ли

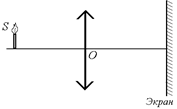Рис. 7.26

мы на экране изображение свечи или нет? И вообще, увидим ли мы на экране хоть что-нибудь? Автор: Здесь, как говорится, возможны варианты. Все дело в том, где именно находятся свеча и экран.

Рассмотрим все возможные случаи.

1. Пусть свеча находится перед фокальной плоскостью линзы (рис. 7.27,а). В этом случае линза дает действительное изображение предмета, и если мы поставим экран именно в той точке, где находится изображение, то мы увидим на экране изображение свечи. Это изображение, как мы уже выяснили в задаче 7.5, будет перевернутым.

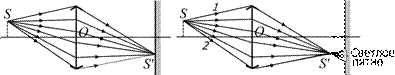
а б

Рис. 7.27

Читатель: А если экран будет находиться чуть ближе к линзе или чуть дальше, чем находится, изображение?

Автор: Если чуть ближе или чуть дальше, то изображение свечи на экране будет слегка размытым. А вот если значительно ближе или дальше, то на экране мы увидим лишь светлое пятно (рис. 7.27, б). Заметим, что размеры пятна будут определяться крайними лучами 1 и 2, проходящими через крайние точки линзы.

Читатель: А если линза дает мнимое изображение?

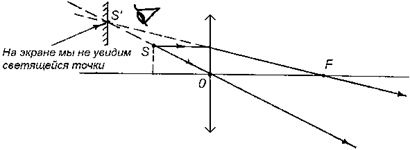
Автор: Хотя мы и можем видеть мнимое изображение, но мы ничего не увидим на экране, если поместим его в том месте, где оно находится. Дело здесь в том, что в данном случае лучи после пре­ломления в линзе расходятся, и в той точке, где находится мнимое изо­бражение, никаких реальных лучей нет (рис. 7.28).

Точно так же, если мы поставим экран за плоским зеркалом в том месте, где находится мнимое изображение предмета, зайдем за зер­кало и посмотрим на экран, то, ясное дело, на экране мы ничего не увидим (рис. 7.29).

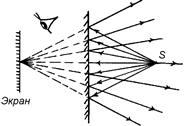Рис. 7.29

Читатель: А отличаются ли чем-нибудь друг от друга точечный источник света и его действительное изображение?

Автор: Из источника лучи распространяются одинаково во всех направле­ниях, а из действительного изображения лучи идут лишь в определенных направлениях. Поэтому источник можно видеть из любого места, а дей­ствительное изображение того же источника только из тех мест, в которые попадают лучи, исходящие из него (рис. 7.30).

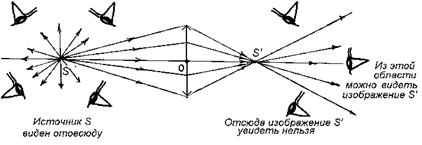
Рис. 7.30

СТОП! Решите самостоятельно: А9–А11, В16, В17, С6–С9, D1.

Рассеивающая линза

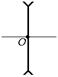Рис. 7.31

Сразу отметим, что на чертеже рассеивающая линза изображается, как по­казано на рис. 7.31.

Экспериментально установлено, что если на рассеивающую линзу напра­вить пучок лучей, параллельных главной оптической оси, то после пре­ломления лучи образуют расходящийся пучок, такой, что продолжения пре­ломленных лучей пересекутся перед линзой в одной точке F (рис. 7.32,а).

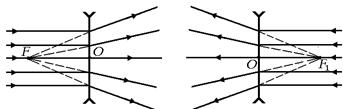
а б

Рис. 7.32

Если на ту же рассеивающую линзу направить пучок параллельных лучей с другой стороны (рис. 7.32,б), то они также образуют после преломления расходящийся пучок, причем продолжения преломленных лучей пересекутся в одной точке F₁. При этом если слева и справа от линзы одна и та же среда (например, стеклянная линза находится в воздухе), то FО = OF₁.

ТочкаF называется передним главным фокусом, а точка F₁ – задним главным фокусом рассеивающей линзы.

Если на рассеивающую линзу направить пучок лучей, параллельных какой-либо побочной оптической оси (рис. 7.33), то после преломления эти лучи образуют пучок расходящихся лучей, продолжения которых пересекутся в одной точке – фокусе линзы f (не главном). Все фокусы рассеивающей линзы находятся на одном расстоянии от главной плоскости линзы и обра­зуют фокальную плоскость. На рис. 7.33 фокальная плоскость изображена прямой AВ.

Рис. 7.33

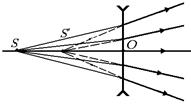Рис. 7.34

Изображение точечного источника в рассеивающей линзе. Если рядом с рассеивающей линзой поместить точечный источник све­та S, то лучи от него попадут на линзу и преломятся таким образом, что из линзы всегда будет выходить расходящийся пучок лучей. При этом продолжения всех преломленных лучей пересекаются в одной точке, образуя мнимое изображение источника (рис. 7.34).

Для построения изображений в рассеивающих линзах обычно используются три основных луча.

1. Луч, проходящий через оптический центр линзы – точку О (рис. 7.35, а). Этот луч проходит через линзу, не преломляясь.

2. Луч, параллельный главной оптической оси. Этот луч преломляется так, что продолжение преломленного луча проходит через главный передний фокус линзы (рис. 7.35, б).

3. Луч, имеющий направление на главный задний фокус линзы. Этот луч после преломления идет параллельно главной оптической оси (рис. 7.35, в).

а б в

Рис. 7.35

Читатель: Насчет третьего луча не совсем понятно. Почему этот луч после преломления идет параллельно главной оптической оси?

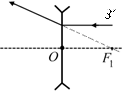Рис. 7.36

Автор: Давайте воспользуемся обратимостью световых лучей. Пустим луч 3¢ справа налево параллельно главной оптической оси (рис. 7.36). Тогда пре­ломленный луч пойдет так, что его продолжение пересечет главный задний фокус линзы. Если луч 3¢ пустить в обратном направлении – слева направо вдоль преломленного луча, то согласно принципу обратимости световых лучей траектория луча не изменится. Вот и получится, что луч, падающий на линзу и имеющий направление на главный задний фокус линзы, после преломления идет параллельно главной оптической оси.

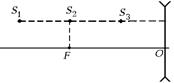Рис. 7.37

Задача 7.7.Постройте изображения источников светаS₁, S₂и S₃ в рассеивающей линзе (рис. 7.37). Положения главных фокусов задано.

Решение.

1. Пустим на линзу луч АВ, параллельный главной оптической оси и про­ходящий через все три источника: S₁, S₂и S₃. Продолжение преломленного луча ВС пройдет через главный передний фокус линзы – точку F (рис. 7.38).

Рис. 7.38

2. Пустим из источниковS₁, S₂и S₃ лучи: 1, 2 и 3 через оптический центр линзы – точку О. Эти лучи пройдут через линзу, не преломляясь.

3. Пересечения лучей 1, 2 и 3 с продолжением луча ВС дадут мнимые изображения источников: точк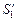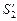и , и .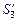

Как видно из рис. 7.38, все изображения находятся перед линзой между передней фокальной и главной плоскостью линзы.

СТОП! Решите самостоятельно: А12, В18, В19, С10.

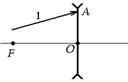Рис. 7.39

Задача 7.8.На рассеивающую линзу падает луч 1 (рис. 7.39). Постройтеход этого луча после преломления. Положения главных фокусов заданы.

Решение.

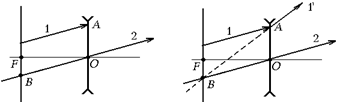
1. Пустим на рассеивающую линзу луч 2, параллельный лучу 1 и про­ходящий через оптический центр линзы – точку О. Этот луч проходит че­рез линзу, не преломляясь (рис. 7.40, а).

2. Проведем фокальную плоскость через точку F параллельно главной плоскости линзы (см. рис. 7.40, а).

3. Лучи 1 и 2 после прохождения через рассеивающую линзу идут так, что их продолжения пересекаются в одной точке – фокусе лин­зы (не главном), который лежит в фокальной плоскости – точке В (см. рис. 7.40, а).

4. Итак, продолжение преломленного луча 1¢ проходит через точки А и В. Проведя через эти точки прямую, получим ход преломленного луча 1¢(см. рис. 7.40, б).

а б

Рис. 7.40

СТОП! Решите самостоятельно: А14, В20, В21, С11.

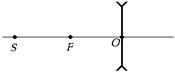Рис. 7.41

Задача 7.9.Постройте изображение точечного источника S, лежащего на главной оп­тической оси рассеивающей линзы (рис. 7.41). Главные фокусные расстояния заданы.

Решение. Пустим из точки S на линзу два луча: луч 1, пересекающий главную плоскость линзы в произвольной точке А, и луч 2, совпадающий с главной оптической осью линзы (рис. 7.42,а). Луч 2 пройдет через линзу, не преломляясь, а ход преломленного луча 1¢ построим точно так же, как мы это сделали в задаче 7.8. Для этого проведем луч 3 через оптический центр – точку О параллельно лучу 1 (рис. 7.42,б). Этот луч пройдет че­рез линзу, не преломляясь.

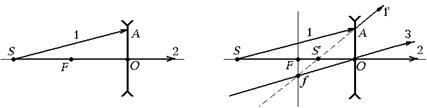
а б

Рис. 7.42

Проведем фокальную плоскость через точку F параллельно главной плоскости линзы, пересечение луча 3 и фокальной плоскости даст побочный фокус f. Затем проведем прямую через точки f и А, получим ход преломленного луча 1¢.

Изображение точечного источника S – точка S¢ – получается пе­ресечением продолжения преломленного луча 1¢ – отрезка fА и глав­ной оптической оси (см. рис. 7.42,б).

СТОП! Решите самостоятельно: В22, D2.

Задача 7.10.Постройте изображения трех небольших предметов: A₁B₁, A₂B₂ и А₃В₃, расположенных перед рассеивающей линзой (рис. 7.43). Положение главных фокусов задано. При построении можно считать, что изображение небольшого отрезка, перпендикулярного главной оптической оси, также является отрезком, перпендикулярным главной оптической оси.

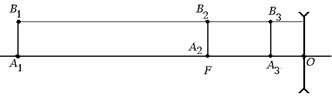Рис. 7.43

Решение.

1. Пустим на линзу луч 1, проходящий через точки В₁, B₂ и В₃ парал­лельно главной оптической оси. После преломления в линзе этот луч пойдет так, что его продолжение пересечет главный передний фокус – точ­ку F (рис. 7.44).

2. Проведем лучи В₁О, В₂О и В₃О. Они пройдут через линзу, не пре­ломляясь. Тогда изображения точек В₁, В₂ и В₃ – точк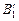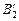и , и 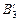– получатся как пересечения продолжения луча 1¢ и лучей В₁О, В₂О и В₃О. (Поскольку лучи В₁О, В₂О и В₃О в линзе не преломляются, то они совпадают со своими продолжениями.)

Как видно из рис. 7.44, все изображения мнимые, прямые и уменьшенные. Причем, чем дальше предмет от линзы, тем меньше его изображение и тем дальше оно от линзы. В то же время все изображения находятся между фокальной плоскостью и главной плоскостью линзы.

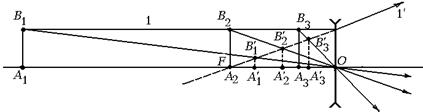
Рис. 7.44

СТОП! Решите самостоятельно: А15, В23, В24.

Задача 7.11.Даны точечный источник света S и его мнимое изображение S¢, полу­ченное в рассеивающей линзе, а также главная оптическая ось линзы (рис. 7.45). Получите построением главные фокусы линзы и главную плос­кость линзы.

Рис. 7.45

Решение.

1. Проведем прямую через точки S и S¢ до пересечения с главной опти­ческой осью. Точка их пересечения – это оптический центр линзы, ведь на луче, проходящем через оптический центр, лежат и источник, и его изображение.

2. Проведем главную плоскость линзы как прямую, перпендикулярную глав­ной оптической оси и проходящую через точку О (рис. 7.46,а).

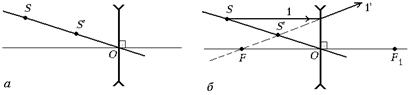
Рис. 7.46

3. Пустим на линзу из точки S луч 1, параллельный главной оптичес­кой оси. Он преломится в линзе так, что его продолжение, во-первых, пройдет через точкуS¢, а во-вторых, пересечет главную оптическую ось в главном переднем фокусе линзы – точке F (рис. 7.46, б).

4. Построим точкуF₁ – главный задний фокус линзы как точку, сим­метричную точкеF относительно главной плоскости линзы (см. рис. 7.46, б).

СТОП! Решите самостоятельно: С12.