Неглавные или побочные фокусы линзы.

Читатель: А что будет, если на собирающую линзу направить параллельный пучок лучей, не параллельный главной оптической оси линзы (рис. 7.6)?

Автор: И в этом случае после преломления лучи соберутся в одной точке, которая называется побочным фокусом линзы.

Читатель: И сколько же у линзы таких побочных фокусов?

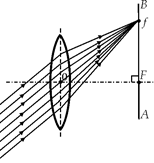Рис. 7.6

Автор: Бесконечно много, ведь параллельные пучки лучей можно направить на линзу под самыми разными углами. Причем все эти фокусы находятся на одинаковом расстоянии от главной плоскости линзы и лежат в одной плоскости, которая называется фокальной плоскостью линзы. Эта плоскость параллельна главной плоскости линзы и проходит через главный фокус линзы F. На рис. 7.6 фокальная плоскость показана прямой АВ.

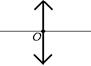Рис. 7.7

Изображение точечного источника в собирающей линзе. Сначала отметим, что на чертежах собирающая линза изображается в виде от­резка с двумя стрелками (рис. 7.7).

Если рядом с собирающей линзой поместить точечный источник света, то лучи от него попадут на линзу, испытают преломление и выйдут наружу. Возникает вопрос: как они будут направлены? Будут ли они сходиться, расходиться или же они образуют параллельный пучок? Тут, как говорится, возможны варианты. Все дело в том, где именно находится источник света.

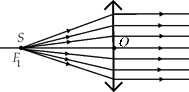Рис. 7.8

1. Пусть точечный источник света S находится в главном переднем фокусе собирающей линзы. Тогда после преломления из линзы выйдет пучок лучей, параллельных главной оптической оси (рис. 7.8). Почему это так?

Воспользуемся обратимостью световых лучей. Если направить на линзу справа налево пучок лучей, параллельных главной оптической оси (см. рис. 7.5,б), то после преломления они пересекутся в главном переднем фокусе линзы. Если изменить направление каждого из этих лучей на противоположное, их траектория не должна измениться. Поэтому лучи, вышедшие из главного переднего фокуса линзы – точки F₁, после преломления образуют пучок лучей, параллельных главной оптичес­кой оси линзы.

2. Пусть источник S не лежит в фокальной плоскости линзы. Тогда возможны два варианта:

1) после преломления лучи соберутся в одной точкеS¢,которая называется действительным изображением источника S (рис. 7.9);

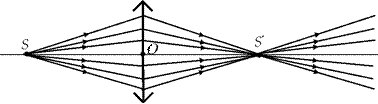
Рис. 7.9

2) после преломления лучи образуют расходящийся пучок, но продолжения преломленных лучей пересекутся перед главной плоскостью линзы в одной точке S ¢, которая называется мнимым изображением источника S (рис. 7.10).

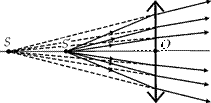Рис. 7.10

Читатель: А как узнать, какое именно изображение – действительное или мнимое – даст конкретный точечный источник света? И где это изображение будет находиться?

Автор: Оказывается, это можно выяснить с помощью построения на бумаге! Прежде всего, заметим, что для того, чтобы получить изображение точечного источника, достаточно проследить ход любых двух лучей, идущих от источника через линзу. Точка пересечения двух преломлен­ных лучей после выхода их из линзы будет действительным изображением точечного источника. А точка пересечения двух продолжений преломленных лучей будет мнимым изображением источника.

Читатель: А почему только двух?

Автор: Потому что мы из опыта знаем, что все лучи, прошедшие через линзу (или их продолжения) пересекаются в одной точке. Так что остальным лучам просто некуда будет деваться: там, где пересекутся любые два лу­ча, пересекутся и все остальные.

Теперь дело за тем, чтобы выделить такие лучи, ход которых после преломления в линзе было бы легко построить. Для построения изображе­ний в собирающих линзах обычно используют три луча (рис. 7.11).

а б в

Рис. 7.11

1. Луч, проходящий через оптический центр линзы точку О. Этот луч проходит через линзу, не преломляясь (рис. 7.11, а).

2. Луч, идущий параллельно главной оптической оси линзы. После прелом­ления этот луч проходит через главный задний фокус линзы – точку F (рис. 7.11, б).

3. Луч, проходящий через передний главный фокус – точку F₁. После преломления этот луч идет параллельно главной оптической оси лин­зы (рис. 7.11, в).

Задача 7.1.Постройте изображения точечного источника S в собирающей линзе. Фокусное расстояние задано (рис. 7.12).

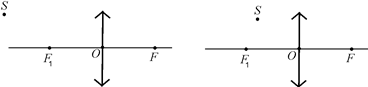
Рис. 7.12

Решение. Случай а.

1. Пустим из источника – точки S – луч 1 через оптический центр лин­зы – точку О. Он пройдет через линзу, не преломившись (рис. 7.13, а).

2. Пустим из точки S луч 2 так, чтобы он проходил через передний главный фокус линзы – точкуF₁. После преломления этот луч (2¢) пойдет параллельно главной оптической оси (см. рис. 7.13, а).

3. Пересечение двух преломленных лучей дает точку S¢. Как видно из рис. 7.13, а, поскольку лучи, прошедшие через линзу, пересеклись, то точкаS' представляет собой действительное изображение точки S.

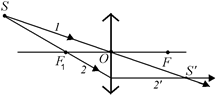
а б

Рис. 7.13

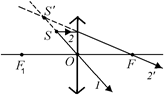
Случай б.

1. Пустим из точки S луч 1 через оптический центр линзы – точку О. Этот луч пройдет через линзу, не меняя своего направления (рис. 7.13, б).

2. Пустим из точки S луч 2 параллельно главной оптической оси. Пре­ломленный луч (2¢) пройдет через главный задний фокус линзы – точку F.

3. Из рис. 7.13, б видно, что за линзой преломленные лучи расходятся. Это значит, что действительного изображения точки S не будет. Продолжим пунктирными прямыми линиями преломленные лучи 1 и 2¢ перед главной плоскостью линзы. Эти продолжения пересекаются в точке S¢. Точка S¢ – это мнимое изображение точечного источника S.

Заметим, что действительное изображение точки S получилось, ког­да она находилась от главной плоскости линзы на расстоянии, большем фокусного, а мнимое изображение получилось в случае, когда источник находился между фокальной плоскостью и главной плоскостью линзы, то есть на расстоянии, меньшем фокусного от главной плоскости линзы.

СТОП! Решите самостоятельно: А1, В1, В2.

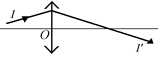Рис. 7.14

Задача 7.2. Даны падающий и преломленный в собирающей линзе лучи 1 и 1¢. Определите построением положение главного заднего фокуса линзы (рис. 7.14).

Решение.

1. Проведем побочную оптическую ось MN параллельно лучу 1 (рис. 7.15, а).

2. Точка пересечения преломленного луча 1¢ и побочной оптической оси MN – это побочный фокус линзы f (падающие на линзу параллельные лучи 1 и MN после преломления пересекаются в фокусе f).

3. Проведем через точку f фокальную плоскость АВ. Точка ее пересе­чения с главной оптической осью – это главный задний фокус F (рис. 7.15,б).

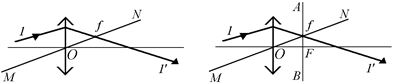
а б

Рис. 7.15

СТОП! Решите самостоятельно: А2, В3, В4.

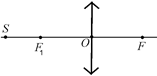Рис. 7.16

Задача 7.3.Постройте изображение точечного источника света S, расположен­ного на главной оптической оси собирающей линзы. Фокусное расстояние задано (рис. 7.16).

Решение.

1. Пустим из точки S луч 1 вдоль главной оптической оси. Он пройдет через линзу, не преломляясь (рис. 7.17, а).

2. Пустим из точки S на линзу луч 2 под произвольным углом к глав­ной оптической оси. Пусть этот луч пересекается с главной плоскостью линзы в точке С (см. рис. 7.17, а).

3. Проведем побочную оптическую ось MN параллельно лучу 2 (рис. 7.17,б).

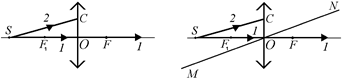
а б

Рис. 7.17

4. Проведем заднюю фокальную плоскость АВ. Точка пересечения фокальной плоскости с побочной оптической осьюMN–это фокус f (не главный) (рис. 7.18, а). В этом фокусе должны пересекаться все лучи, падающие на линзу параллельно побочной оптической осиMN.

5. Проведем прямую через точки С и f. Получим ход преломленного луча 2¢. Точка пересечения луча 2¢ с лучом 1, совпадающим с главной опти­ческой осью, – это действительное изображение источника S – точка S¢. (рис. 7.18, б).

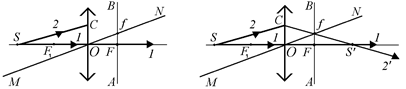
а б

Рис. 7.18

СТОП! Решите самостоятельно: А3, А4, В5, В6, С1.

Задача 7.4.Дан точечный источник S, его изображение в собирающей линзе S¢ и главная оптическая ось линзы (рис. 7.19). Получите построением главную плоскость и главные фокусы линзы.

Решение.

1. Проведем прямуюSS¢, она пересечет главную оптическую ось в точке О. Точка О – это оптический центр линзы. Восстановив перпендикуляр к главной оптической оси из точки О, получим главную плоскость линзы (рис. 7.20,а).

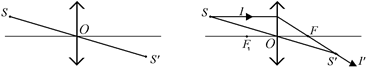
а б

Рис. 7.20

Читатель: Все-таки не совсем понятно, почему точка О – это главный оп­тический центр линзы?

Автор: Мы знаем, что через оптический центр луч идет, не преломляясь. Значит, если луч идет от источника S к его изображению S¢ по пря­мой, то эта прямая проходит через оптический центр. А так как глав­ная оптическая ось также проходит через оптический центр, то ясно, что оптический центр – это точка пересечения главной оптической оси с отрезком SS¢.

2. Пустим из точки S на линзу луч 1 параллельно главной оптической оси. Преломленный луч 1' должен пройти через главный задний фокус линзы и попасть в точку S¢. Точка пересечения луча 1' с главной оптиче­ской осью – это и есть главный задний фокус линзы – точка F (рис. 7.20, б).

Главный передний фокус F₁ – это точка, симметричная точке F отно­сительно главной плоскости линзы: F₁О = OF.

СТОП! Решите самостоятельно: В7.

Построение изображений предметов в собирающей линзе. Экспери­ментально установлено, что небольшие отрезки, перпендикулярные главной оптической оси, в качестве изображения (действительного или мнимого) дают отрезки, перпендикулярные главной оптической оси.

Задача 7.5. Постройте изображения отрезков в собирающей линзе (рис. 7.21). Фокусные расстояния заданы.

а б

Рис. 7.21

Решение. Так как изображениями во всех случаях будут отрезки, перпендикулярные главной оптической оси, то достаточно построить изображения только верхних точек каждого из отрезков. Имея изображение верхней точки, все изображение мы получим, опустив перпендикуляр из изображения вер­хней точки на главную оптическую ось.

Случай а. В этом случае все отрезки удалены от главной плоскости линзы на рас­стояние, большее фокусного.

1. Пустим на линзу один общий для всех трех отрезков луч 1, параллельный главной оптической оси и проходящий через верхние концы всех отрезков. Преломленный луч 1¢ пройдет через главный задний фокус линзы F (рис. 7.22).

2. Из верхних точек отрезков пустим на линзу лучи А, В, С, проходящие через оптический центр линзы – точку О. Эти лучи пройдут линзу, не преломляясь.

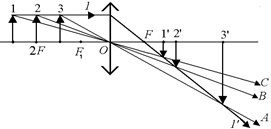
Точки пересечения луча 1¢ с лучами А, В и С дадут изображения верхних концов отрезков 1, 2 и 3. Опустив из этих точек перпендикуляры на глав­ную оптическую ось, получим изображения отрезков: 1¢, 2¢ и 3¢ (см. рис. 7.22).

Заметим, что изображения всех отрезков получились действительными и перевернутыми, причем изображение отрезка 3 получилось увеличенным, а изображение отрезка 1 – уменьшенным. Длина изображения 2¢ оказа­лась в точности равной длине отрезка 2. (Отрезок 2 находился на двойном фокусном расстоянии от главной плоскости линзы).

Заметим также, что если бы мы перемещали отрезок 1 по направлению к линзе (из положения 1 – в положение 2, а из положения 2 – в по­ложение 3), то его изображение при этом удалялось бы от линзы, постепенно увеличиваясь в размерах (из положения 1¢ – в положение 2¢, из положения 2¢ – в положение 3¢, см. рис. 7.22).

Случай б.

1. Проведем, как и в случае а, луч 1, параллельный главной оптической оси через верхние концы отрезков 1, 2 и 3. Преломленный луч 1¢ пройдет через главный задний фокус линзы F.

2. Из верхних концов отрезков 1, 2 и 3 пустим через оптический центр линзы – точку О лучи А, В и С (рис. 7.23). Эти лучи пройдут через линзу, не преломляясь. Из рис. 7.23 видно, луч 1¢ и лучи А, В и С за главной плоскостью линзы не пересекаются. Это значит, что дей­ствительного изображения верхних концов отрезков не будет. Значит, должны получиться мнимые изображения верхних концов отрезков.

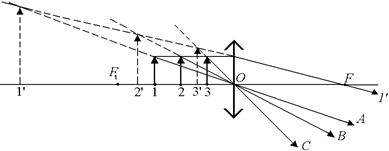
3. Построим пунктирными линями продолжения преломленных лучей 1¢, А, В и С перед главной плоскостью линзы. Точки пересечения продолжений лучей А, В и С с продолжением луча 1 дадут мнимые изображения верхних концов отрезков 1¢, 2¢ и 3¢. Опустив из этих точек перпендикуляры на главную оптическую ось, получим мнимые изображения отрезков 1¢, 2¢ и 3¢.

Отметим следующее: все изображения отрезков получились мнимыми, прямыми (т.е. не перевернутыми) и увеличенными. (Отрезки, выступав­шие в качестве источников, находились между фокальной плоскостью и главной плоскостью линзы, т.е. на расстоянии от линзы, меньшем фо­кусного).

Если бы мы стали перемещать отрезок 1 по направлению к линзе (из положения 1 – в положение 2, из положения 2 – в положение 3), то изображение при этом, во-первых, приближалось бы к линзе, а во-вто­рых, уменьшалось бы в размерах (из положения 1¢ – в положение 2 ¢, из положения 2' – в положение 3¢ (см. рис. 7.23).

СТОП! Решите самостоятельно: А5–А8, В8–В12, С2–С4.

Задача 7.6.Постройте изображение отрезка АВ в собирающей линзе (рис. 7.24). Фо­кусные расстояния заданы.

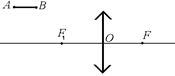Рис. 7.24

Решение. Экспериментально установлено, что изображение любого небольшого от­резка в собирающей линзе представляет собой отрезок прямой. (Изо­бражение может быть при этом как мнимым, так и действительным.) Поэтому для того чтобы построить изображение отрезка АВ, достаточно построить изображения точек А и В и соединить эти изображения от­резком прямой.

1. Продолжим главную плоскость линзы вверх (пунктирная линия на рис. 7.25). Тогда можно будет пустить луч, идущий одновременно из точек А и В параллельно главной оптической оси так, чтобы он преломился в линзе.

Рис. 7.25

Читатель: Но ведь на самом деле такой луч пройдет мимо нашей линзы! Какое же мы имеем право удлинять линзу? Ведь тогда получится то, чего на самом деле нет!

Автор: Не забывайте, что все лучи, исходящие из любого точеч­ного источника, после преломления в линзе либо сами пересекаются в одной точке, если изображение действительное, либо в одной точке пересекаются их продолжения, если изображение мнимое. Увеличив раз­мер линзы, мы лишь увеличим число лучей, проходящих через лин­зу, но место нахождения изображения мы этим никак не изменим. Поэтому если нам удобно на чертеже увеличить размер линзы, чтобы нарисовать ход какого-нибудь удобного нам луча, мы имеем право это сделать.

2. Пустим на линзу луч 1, параллельный главной оптической оси, иду­щий одновременно через точки А и В (см. рис. 7.25). Преломленный луч 1¢, пройдет через главный задний фокус линзы F.

3. Пустим из точки А луч 2, а из точки В луч 3 так, чтобы они про­ходили через оптический центр – точку О. Эти лучи пройдут через линзу, не преломляясь (см. рис. 7.25).

4. Точка пересечения луча 2 и луча 1¢ (точка А¢) – это действительное изображение точки А, а точка пересечения луча 3 и луча 1¢ (точка В¢) – ­это действительное изображение точки В (см. рис. 7.25). Отрезок А¢В¢ является изображением отрезка АВ.

Читатель: Если линзу в целях удобства можно увеличивать в размерах, то, наверное, ничего не изменится и в том случае, если линзу уменьшить в раз­мерах (например, закрыв часть ее поверхности непрозрачным экраном)?

Автор: Конечно. Местонахождение изображения при этом не изменится, изменится только яркость изображения.

СТОП! Решите самостоятельно: В14, В15, С5.