Область наблюдения изображения

В плоском зеркале

Задача 2.14.Укажите на рисунке область, из которой можно наблюдать изображение точечного источника света S в плоском зеркале АВ (рис. 2.28).

Рис. 2.28

Решение.Область наблюдения изображения – это часть пространства, в которую попадают отраженные от зеркала лучи.

1. Построим изображение S¢ для случая а (рис. 2.29, а). Проведем лучи S¢B и S¢А, которые являются "крайними" лучами, отраженными от зеркала АВ. Любой другой луч, исходящий от источника S и отраженный от зеркала АВ (например, луч 1) будет находиться между лучами S'A и S¢B.

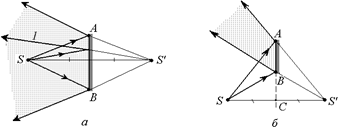Рис. 2.29

Таким образом, область наблюдения изображения – это часть пространства между зеркалом АВ и лучами S'B и S'А (на рис. 2.29, а она показана штриховкой).

2. В случае б для построения изображения S' мысленно продолжим зеркало АВ вниз (пунктирная линия ВС) и построим точку S', симметричную точке S относительно прямой ВС (рис. 2.29, б).

Читатель: Это как-то непонятно. Разве "мысленное" зеркало ВС (которого на самом деле нет) может дать изображение S¢ ?

Автор: Положение изображения S не зависит от того, какова длина зеркала. Ведь мы же с Вами уже выяснили, что все лучи, исходящие из точечного источника и отраженные от плоского зеркала, идут таким образом, что их продолжения пересекаются в одной единственной точке S¢, симметричной источнику S относительно плоскости зеркала. Поэтому для удобства построения мы вполне можем продлить плоскость зеркала АВ до нужных нам размеров.

После того, как изображение S¢ построено, проведем "крайние" лучи S'В и S¢А. Область наблюдения лежит между зеркалом АВ и этими лучами (она показана штриховкой на рис. 2.29, б). Заметим, что из точки S ее изображение S¢ увидеть нельзя.

Задача 2.15. Постройте область наблюдения изображения отрезка АВ в плоском зеркале MN (рис. 2.30, а).

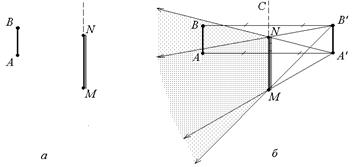
Рис. 2.30

Решение.Продолжим плоскость зеркала MN немного вверх (пунктирная линия NС) и построим изображения точек А и В. Для этого построим точки А¢ и В¢, симметричные точкам А и В относительно прямой MNC.

Построим аналогично тому, как мы это делали в задаче 2.14, области наблюдения изображений А¢ и В¢ в зеркале MN, для чего проведем "крайние лучи" А¢М, А¢N, В¢М и В¢N (рис. 2.30, б). Изображение А¢В¢ можно будет наблюдать из тех точек пространства, из которых можно одновременно наблюдать точки А¢ и В¢. Эта область показана на рис. 2.30, б двойной штриховкой.

СТОП! Решите самостоятельно: А16, В20, В21, С12.

Задача 2.16. Чем ближе человек стоит к окну, тем больший участок улицы ему виден. Но если он видит в зеркале, висящем вертикально на стене, свое отражение только до колен, то все попытки увидеть больше, подойдя к зеркалу, остаются безуспешными. Почему?

Решение. Пусть человек высотой Н находится на расстоянии l от зеркала высотой а, смотрит на свое изображение и видит лишь часть своей фигуры высотой h (рис. 2.31).

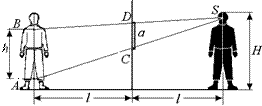Рис. 2.31

Как видно из рисунка, DSCD ∾ DSAB, поэтому

,

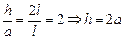т.е. величина видимой части изображения не зависит ни от высоты человека, ни от его расстояния до зеркала и всегда равна удвоенной высоте зеркала! Поэтому как бы близко человек не подходил к зеркалу, он всегда увидит только часть фигуры, и размер этой части всегда один и тот же – удвоенная высота зеркала.

СТОП! Решите самостоятельно: В22, В23, С13–С15.

Солнечный зайчик

Автор: Наверное, вам не раз приходилось видеть и даже пускать солнечных «зайчиков». Как Вы думаете, что такое солнечный «зайчик» на стене?

Читатель: По-моему, это то место, куда зеркалом направляют солнечный луч.

Автор: Вы правы. Но давайте сформулируем эту мысль четче. Зеркало создает мнимое изображение солнца (рис. 2.32). Это изображение, как мы знаем, можно видеть только из области наблюдения изображения. Солнечный «зайчик» – это место на стене, откуда, посмотрев на зеркало, можно увидеть изображение солнца.

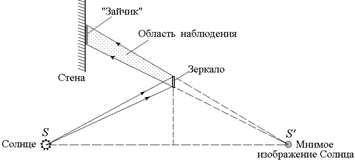
Рис. 2.32

Заметим, что «зайчик» можно получить не только от солнца, но и от обычной лампочки.

«Зайчик» от точечного источника света. Попробуем выяснить, зависит ли форма и размеры «зайчика» от формы, размеров и положения зеркала, а также от расстояния зеркала до экрана.

Рис. 2.33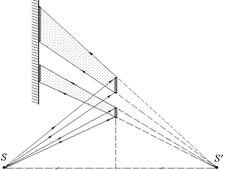

Как видно из рис. 2.33, чем больше зеркало, тем больше «зайчик».

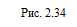
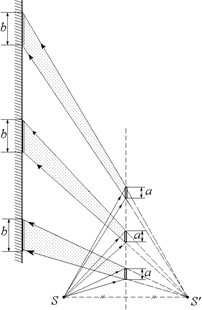Ясно, что форма «зайчика» зависит также от формы зеркала. Если изображение S¢ расположить настолько далеко от зеркала, что лучи, проходящие через зеркало, практически параллельны, то как видно из рис. 2.34, от расстояния до источника и от угла падения лучей источника на зеркало размер «зайчика» не зависит.

Если же расстояние от S¢ до зеркала невелико, то размеры «зайчика» будут тем больше, чем меньше это расстояние.

СТОП! Решите самостоятельно: С16, С17.

«Зайчик» от источника конечных размеров. Солнце не является точечным источником света, поэтому область наблюдения изображения Солнца в зеркале зависит от размеров зеркала. Чем больше зеркало, тем больше область, из которой можно увидеть изображения Солнца полностью. На рис. 2.35 видно, что область наблюдения Солнца для зеркала 2 значительно больше, чем для зеркала 1 (область наблюдения показана штриховкой).

Кроме того, из рис. 2.35 видно, что чем ближе к зеркалу находится экран, тем больше на этом экране область, из которой изображение Солнца видно полностью. А это значит, что «зайчик» на таком экране получится ярким с достаточно четкими краями и близкий по форме к форме зеркала (экран 1 на рис. 2.25).

Если же экран стоит далеко от зеркала, то область на экране, из которой видно изображение Солнца, целиком становится меньше, но зато увеличивается область, из которой видна часть изображения Солнца (экран 2 на рис. 2.35). Это значит, что «зайчик» становится большим, слабым и с нечеткими краями.

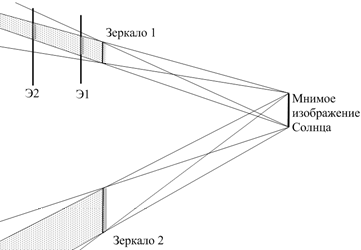
Рис. 2.35

СТОП! Решите самостоятельно: В24–В26.