Уравнение бегущей волны. Рассмотрим волну, «бегущую» по длинному тонкому резиновому шнуру

Рассмотрим волну, «бегущую» по длинному тонкому резиновому шнуру. Ось Х направим вдоль шнура, а начало отсчета возьмем в левом конце шнура (рис. 6.7).

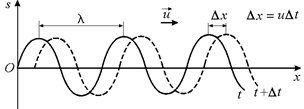Рис. 6.7

Будем обозначать смещение любой колеблющейся точки шнура от положения равновесия буквой s. Ясно, что величина s может быть как положительной, так и отрицательной.

Заставим конец шнура (точка х = 0) совершать гармонические колебания с циклической частотой w. Пусть эти колебания будут проходить по закону

s = s_msinwt. (6.3)

Здесь s_m – амплитуда колебаний (рис. 6.8,а).

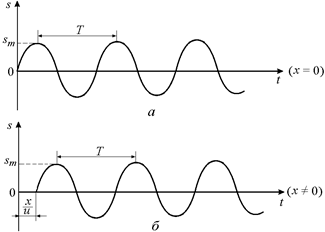
Рис. 6.8

Читатель: А почему Вы записали s = s_msinwt, а не s = s_mcoswt?

Автор: Для разнообразия: ведь между функциями у = sinx и y = = cosx разница очень небольшая: .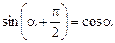

Но если мы возьмем уравнение s = s_msinwt, то это значит, что в начальный момент t = 0 смещение s было равно нулю: s = = s_msin0 = 0.

Если взять уравнение s = s_mcoswt, то это значит, что в начальный момент t = 0 смещение s было равно амплитуде: s = s_mcos0 = s_m, т.е. точка находилась в крайнем верхнем положении.

Колебания распространяются вдоль шнура со скоростью и и в точку с произвольной координатой х «придут» спустя время

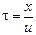. (6.4)

Эта точка также начнет совершать вынужденные гармонические колебания с частотой w, но с запаздыванием на время t (рис. 6.8,б). Если пренебречь затуханием, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой j = w(t – t):

s = s_msin[w(t – t)] = 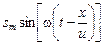. (6.5)

Это и есть уравнение бегущей волны, распространяющейся в положительном направлении оси Х. Оно позволяет нам определить смещение s точки с любой координатой х в любой момент времени t.

В случае, когда начальная фаза колебаний в точке х = 0 равна не нулю, а произвольной величине j₀, уравнение бегущей волны запишется так:

.

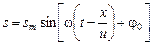Если взять, например, 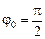, получим:

,

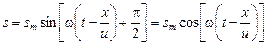так как .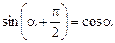

Амплитуда колебаний s_m называется амплитудой волны. Величина, стоящая под знаком синуса, называется фазой волны. В общем случае фаза равна

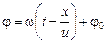. (6.6)

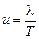Подставляя в формулу (6.6) значения и , получим

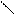
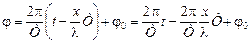Þ

. (6.7)

Если j₀ = 0, то получим следующую форму записи уравнения бегущей волны:

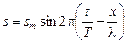. (6.8)

Если в этой формуле заменить t на t + Т, получим

,

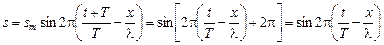а если заменить х на х + l, получим

.

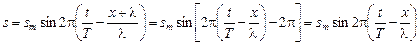Иными словами, функция s(x,t) = 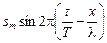обладает периодичностью по времени при фиксированном х:

s(x, t + T) = s(x, t)

и периодичностью по координате при фиксированном t:

s(x+l, t) = s(x, t).

Итак, мы выяснили, что в бегущей волне все точки (участки шнура) совершают вынужденные колебания с одним и тем же периодом, но с разными фазами.

Две точки с координатами х₁ и х₂ имеют в данный момент времени t разность фаз

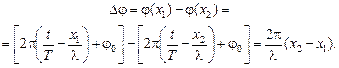
Запомним:

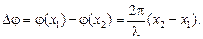(6.9)

Заметим, что если разность координат равна целому числу длин волн: х₂ – х₁ = lk, где k = 1, 2, 3…, то

,

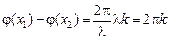следовательно, точки х₁ и х₂ колеблются синфазно: их смещения в любой момент времени равны, так как sinj = sin(j + 2pk). А если разность координат равна нечетному числу полуволн 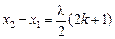, где k = 0, 1, 2, …, то

.

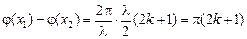Это значит, что смещения точек х₁ и х₂ одинаковы по величине и противоположны по знаку: х₁ = –х₂, потому что

sin(j + (2k + 1)p) = sin(j + p + 2pk) = sin(j + p) = –sinj.

Иными словами, если разность координат двух точек волны равна нечетному числу полуволн, то эти точки колеблются в противофазе. Например, на рис. 6.4 в противофазе колеблются шары 1 и 7, 2 и 8, 3 и 9.

Задача 6.2. В среде распространяется волна со скоростью и = =720 м/с при частоте источника n = 600 Гц. Определите разность фаз колебаний в двух точках, отстоящих друг от друга на расстояние Dх = 0,2 м. Все значения считать точными.

и = 720 м/с n = 600 Гц Dх = 0,2 м	Решение. Воспользуемся формулой (6.9) 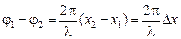. (1) Вспомним формулу (6.2): и = ln Þ l = и/n.
j1 – j2 = ?

Подставим значение l в (1):

.

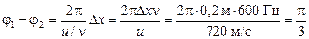Ответ: .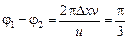

СТОП! Решите самостоятельно: А5, В2–В4, С1, С2.