Задачи очень трудные. D1. Каждая из п точек соединена со всеми остальными точками проволоками, имеющими сопротивление R
D1. Каждая из п точек соединена со всеми остальными точками проволоками, имеющими сопротивление R. К двум из этих точек подключается батарея с ЭДС õи внутренним сопротивлением r. Найти силу тока, протекающего через источник.
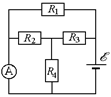 Рис. 13.35
Рис. 13.35
|
D2. Как измерить величину неизвестного сопротивления, имея вольтметр и амперметр с неизвестными внутренними сопротивлениями?
D3. Определите силу тока IА через амперметр (рис. 13.35), если сопротивления резисторов: R1= = 20 Ом; R2 = R4= 8 Ом; R3= 1 Ом. ЭДС источника õ= 50 В, его внутреннее сопротивление r = 1 Ом. Сопротивление амперметра можно считать пренебрежимо малым.
D4. Чтобы определить место повреждения изоляции двухпроводной телефонной линии длиной L = 4 км,кодному ее концу присоединили батарею с ЭДС, õ =15 В. При этом оказалось, что если провода у другого конца линии разомкнуты, ток через батарею I1 = 1 А,если замкнуты накоротко, то ток через батарею I2 = 1,8 А. Найти место повреждения и сопротивление R изоляции в месте повреждения. Сопротивление каждого провода линии 5 Ом. Сопротивлением батареи пренебречь.
D5. К одному концу двухпроводной линии передачи электроэнергии подсоединен источник постоянной ЭДС, а к другому – потребитель с сопротивлением R0. В линии произошло повреждение изоляции, в результате чего ток через источник возрос в два раза, а ток через нагрузку R0упал в восемь раз. Найти сопротивление изоляции в месте повреждения, если длина каждого провода линии равна L, а сопротивление единицы длины провода равно r.
Расчет сложных электрических цепей
Правила Кирхгофа
Если в одной точке электрической цепи сходится более двух проводников, то такая точка называется точкой разветвления или узлом.
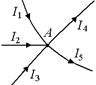 Рис. 14.1
Рис. 14.1
|
На рис. 14.1 в точке разветвления А сходятся 5 проводников. Обозначим силу тока в них I1, I2, I3, I4 и I5. Из рисунка видно, что токи I1, I2, I3 направлены к узлу и за время Dt приносят в этот узел заряд
Dq1 = (I1 + I2 + I3)Dt.
Токи I4 и I5 направлены от узла и за время Dt уносят из узла заряд Dq2 = (I4 + I5)Dt.
Поскольку в узле заряд накапливаться не может, то
Dq1 = Dq2 Þ (I1 + I2 + I3)Dt = (I4 + I5)Dt Þ I1 + I2 + I3 = I4 + I5 Þ
I1 + I2 + I3 – I4 – I5 = 0 (1)
Если считать силу тока алгебраической величиной, имеющей знак «плюс», если ток подходит к узлу, и знак «минус», если ток направлен от узла, то равенство (1) можно записать в виде
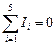 .
.
Если в узле сходятся N токов, то
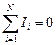 . (14.1)
. (14.1)
Это равенство называется первым правилом Кирхгофа: алгебраическая сумма сил токов в проводниках, сходящихся в узле, равна нулю.
Вспомним закон Ома для участка цепи, содержащего ЭДС (рис. 14.2):
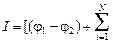 õi] / (
õi] / ( 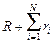 ). (14.2)
). (14.2)
Рис. 14.2 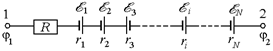
Здесь õi – алгебраическая величина: õi > 0, если ЭДС «направлена» от 1 к 2 (например, õ1 и õ2 на рис. 14.2) и õi < 0, если она «направлена» от 2 к 1 (например, õ3 на рис. 14.2).
Величина силы тока I тоже алгебраическая величина: если I > 0, значит, ток направлен от 1 к 2, а если I < 0, то ток течет от 2 к 1. Перепишем равенство (14.2) в виде
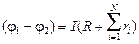 –
– 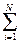 õi. (14.3)
õi. (14.3)
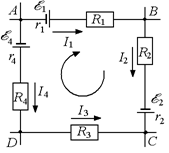 Рис. 14.3
Рис. 14.3
|
В общем случае электрическая цепь может быть образована несколькими источниками тока и резисторами, соединенными произвольным образом. Сложную электрическую цепь можно разбить на ряд отдельных замкнутых контуров.
Рассмотрим произвольно выбранный замкнутый контур ABCD (рис. 14.3). Обозначим потенциалы узлов А, В, С и D соответственно через jА, jВ, jС и jD.
Выберем направление обхода контура – по часовой стрелке (см. рис. 14.3). Запишем уравнения закона Ома для участка цепи, содержащего ЭДС для участков АВ, ВС, CD и AD соответственно:
| АВ: jА – jВ = I1(R1 + r1) – õ1; ВС: jВ – jС = I2(R2 + r2) – õ2; CD: jC – jD = I3R3 ; DA: jD – jA = I4(R4 + r4) – õ4. | (14.4) |
Заметим, что здесь õ1 > 0, õ2 > 0, õ4 < 0, I1 > 0, I2 > 0, I3 < 0, I4 < 0. Сложим почленно равенства (14.4) и получим
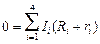 –
– 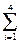 õi Þ
õi Þ
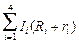 =
= 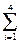 õi. (14.5)
õi. (14.5)
(Заметим, что поскольку на участке CD отсутствует источник тока, то õ3 = 0 и r3 = 0.)
Это и есть второе правило Кирхгофа: алгебраическая сумма падений напряжений в ветвях замкнутого контура равна алгебраической сумме ЭДС, действующих в этом же контуре.
В более общем виде второе правило Кирхгофа можно записать так:
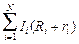 =
= 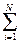 õi. (14.6)
õi. (14.6)
Задача 14.1. Два элемента, ЭДС которых õ1 = 2 В и õ2 = 1 В, соединены по схемам, показанным на рис. 14.4. Сопротивление резистора R = 0,5 Ом. Внутренние сопротивления элементов одинаковы и равны r = 1,0 Ом каждое. Определить силы токов в элементах и резисторе. Все значения считать точными.
| õ1 = 2 В õ2 = 1 В R = 0,5 Ом r = 1,0 Ом | 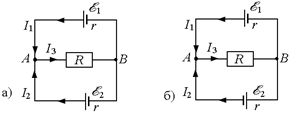 Рис. 14.4
Рис. 14.4
|
| I1 = ? I2 = ? I3 = ? | |
Решение. Сначала предположим, что токи идут так, как показано на рис. 14.4. (Как они идут на самом деле, мы пока не знаем.)
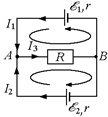 Рис. 14.5
Рис. 14.5
|
1. Рассмотрим случай на рис. 14.4,а. Возьмем два контура (рис. 14.5) и применим к каждому из них второе правило Кирхгофа, получим:
для верхнего контура
I1r + I3R = õ1, (1)
для нижнего контура
I2r + I3R = õ2. (2)
Для узла А применим первое правило Кирхгофа:
I1 + I2 = I3. (3)
Теперь решим полученную систему уравнений (1)–(3) относительно неизвестных величин I1, I2, I3. Чтобы избежать громоздких алгебраических преобразований, сразу подставим численные значения õ1, õ2, r и R:
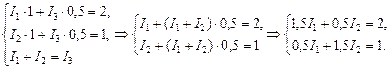
Умножим последнее уравнение на 3:
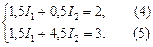
Из (4) вычтем (5) и получим: 0,5I2 – 4,5I2 = 2 – 3 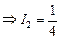 . Подставим это значение в (4):
. Подставим это значение в (4):
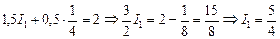 .
.
Подставим полученные значения I1 и I2 в формулу (3) и найдем I3:
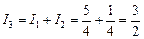 .
.
Итак, мы получили значения сил токов:
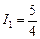 А,
А, 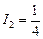 А,
А, 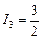 А.
А.
Как видим, все значения получились положительными, значит, мы правильно указали направление токов на рис. 14.4,а.
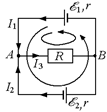 Рис. 14.6
Рис. 14.6
|
2. Рассмотрим случай на рис. 14.4,б. Для разнообразия, возьмем другую пару контуров (рис. 14.6) и применим к каждому из них второе правило Кирхгофа, получим:
для малого контура
I1r + I3R = õ1, (6)
для большого контура
I1r – I2r = õ1 + õ2. (7)
Для узла А применим первое правило Кирхгофа:
I1 + I2 = I3. (8)
Теперь решим полученную систему уравнений (6)–(8) относительно неизвестных величин I1, I2, I3. Подставим в уравнения (6)–(8) численные значения õ1, õ2, r и R:
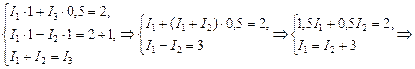
1,5(I2 + 3) + 0,5I2 = 2 Þ 2I2 = –2,5 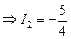 .
.
Тогда 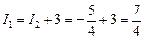 ,
, 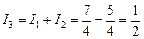 .
.
Итак, мы получили значения сил токов:
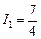 А,
А, 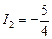 А,
А, 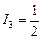 А.
А.
Так как значение I2 получились отрицательным, значит, ток I2 течет не так, как показано на рис. 14.4,б, а в противоположном направлении.
Ответ: а) 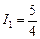 А,
А, 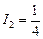 А,
А, 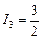 А; б)
А; б) 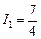 А,
А, 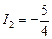 А,
А, 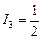 А.
А.
СТОП! Решите самостоятельно: А2, В1, В2, С1, С4, С5.
Дата добавления: 2016-04-11; просмотров: 1931;
