Электрическое поле в диэлектрике
Мы знаем, что согласно закону Кулона два точечных заряда q1 и q2, расположенных на расстоянии r друг от друга, взаимодействуют в вакууме с силой, равной по величине
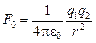 .
.
Однако если эти же заряды поместить на таком же расстоянии друг от друга не в вакууме, а в какой-либо среде (воде, воздухе, керосине, спирте и т.п.), то сила их взаимодействия уменьшится и станет равной
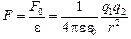 , (1.1)
, (1.1)
где e – постоянная для данной среды величина, называемая диэлектрической проницаемостью среды; e – величина безразмерная: [e] = 1.
| Т а б л и ц а 1.1 | |
| Вещество | e |
| Воздух (при 0 °С и 760 мм рт. ст.) | 1,000594 |
| Керосин | 2,1 |
| Эбонит | 2,7 |
| Кварц | 4,5 |
| Спирт этиловый | |
| Вода | |
| Сегнетова соль | 1,0×104 |
Диэлектрическая проницаемость среды – это физическая величина, характеризующая электрические свойства вещества и показывающая, во сколько раз сила взаимодействия зарядов в данной среде меньше силы их взаимодействия в вакууме.
В табл. 1.1 приведены значения диэлектрической проницаемости некоторых веществ.
Задача 1.1. Два заряда взаимодействуют в воде с силой F1 = 3,0×10–4 Н. С какой силой они будут взаимодействовать в этиловом спирте?
| F1 = 3,0×10–4 Н | Решение. По табл. 1.1 диэлектрическая проницаемость воды e1 = 81, а этилового спирта e2 = 27. |
| F2 = ? |
Согласно формуле (1.1) 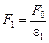 ,
, 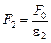 , где F0 – сила взаимодействия зарядов в вакууме. Из этих формул нетрудно получить:
, где F0 – сила взаимодействия зарядов в вакууме. Из этих формул нетрудно получить:
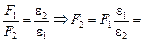 3,0×10–4 Н
3,0×10–4 Н 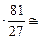 9,0×10–4 Н.
9,0×10–4 Н.
Ответ: 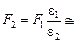 9,0×10–4 Н.
9,0×10–4 Н.
СТОП! Решите самостоятельно: А1, А2, А3, В1.
Задача 1.2. На каком расстоянии от шарика А (рис. 1.1,а), погруженного в керосин, должен быть расположен стальной шарик В объемом V = 9,0 мм3, чтобы он находился в равновесии? Заряд шарика А равен q1 = 7,0 нКл, а заряд шарика В q2 = –2,1 нКл. Плотность керосина rк = 0,80×103 кг/м3, плотность стали rст = 7,8×103 кг/м3.
| V = 9,0 мм3 = 9,0×10–9 м3 q1 = 7,0 нКл = 7,0×10–9 Кл q2 = –2,1 нКл = –2,1×10–9 Кл rк = 0,80×103 кг/м3 rст = 7,8×103 кг/м3 | а  б б 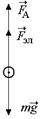 Рис. 1.1
Рис. 1.1
|
| r = ? | |
Решение. На шарик В действуют три силы: сила тяжести 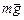 , сила Архимеда
, сила Архимеда 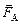 и сила Кулона
и сила Кулона 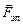 (рис. 1.1,б). Так как шарик В покоится, то
(рис. 1.1,б). Так как шарик В покоится, то
FА + Fэл = mg Þ 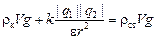 , (1)
, (1)
где k = 9×109 (Н×м2)/Кл2; e = 2,1 – диэлектрическая постоянная керосина по табл. 1.1. Из (1) находим r:
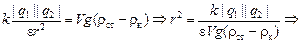
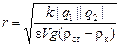
| (СИ) = | 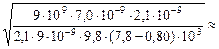
|
» 1,0×10–2 м = 1,0 см.
Ответ: 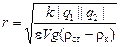 » 1,0 см.
» 1,0 см.
СТОП! Решите самостоятельно: В2, С1.
Задача 1.2. Два шарика из одного материала одинаковых радиусов и масс подвешены в вакууме в одной точке на нитях одинаковой длины. Когда их заряжают одноименными зарядами, нити расходятся на некоторый угол. Какова должна быть диэлектрическая проницаемость жидкого диэлектрика, чтобы при погружении в него этой системы угол расхождения нитей не изменился? Отношение плотности материала шариков к плотности жидкого диэлектрика равно 3.
| e1 = 1 rш/rж = 3 | 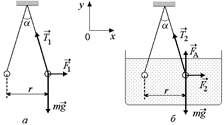 Рис. 1.2 Рис. 1.2
|
| e2 = ? | |
Решение. В вакууме на каждой из шариков действуют три силы: сила тяжести 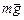 , сила натяжения нити
, сила натяжения нити 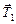 и сила Кулона
и сила Кулона 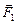 (рис. 1.2,а). В жидком диэлектрике к этим силам добавляется еще и сила Архимеда
(рис. 1.2,а). В жидком диэлектрике к этим силам добавляется еще и сила Архимеда 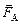 , причем сила натяжения
, причем сила натяжения 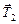 и сила Кулона
и сила Кулона 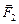 уменьшаются по величине (рис. 1.2,б).
уменьшаются по величине (рис. 1.2,б).
Для первого случая справедливо
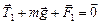 , (1)
, (1)
для второго случая
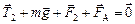 , (2)
, (2)
Запишем уравнения (1) и (2) в проекциях на оси х и у:
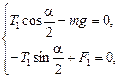 (3)
(3) 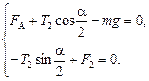 (4)
(4)
Решим полученную систему их четырех уравнений. Для этого перепишем системы (3) и (4) в виде
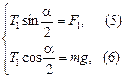
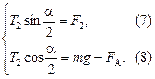
Разделим уравнение (5) на (6), а (7) на (8) и получим
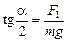 , (9)
, (9) 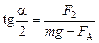 . (10)
. (10)
Приравняем правые части уравнения (9) и (10)
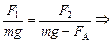
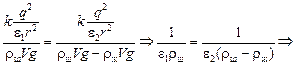
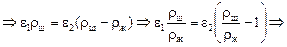
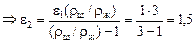 .
.
Ответ: 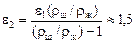 .
.
 СТОП! Решите самостоятельно: В3, В4, С3.
СТОП! Решите самостоятельно: В3, В4, С3.
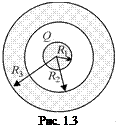
Задача 1.4. Металлический заряженный шар помещен в центре толстого сферического слоя, изготовленного из диэлектрика с проницаемостью e = 2 (рис. 1.3).
1. Нарисовать картины силовых линий внутри и вне сферического слоя.
2. Начертить графики зависимости напряженности поля и потенциала от расстояния до центра сферы.
Решение. 1. Нарисуем сначала картину силовых линий для заряженного шара в отсутствии диэлектрика (рис. 1.4,а).
а 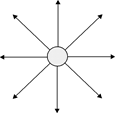 б
б 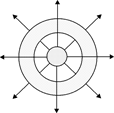
Рис. 1.4
Добавление сферического слоя из диэлектрика приведет к тому, что напряженность поля в той области, где находится диэлектрик, ослабнет в e = 2 раза, а в остальной части пространства не изменится. Это значит, что число силовых линий в сферическом слое в 2 раза меньше, чем вне его (рис. 1.4,б).
2. Сначала изобразим график Е(r) для случая заряженного металлического шара в отсутствии диэлектрика, а затем уменьшим величину Е(r) в интервале (R2, R3) в 2 раза (рис. 1.5,а).
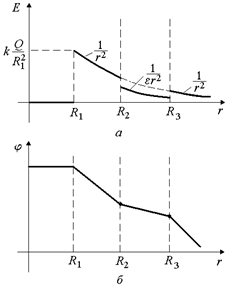
Рис. 1.5
3. График j(r) будем строить, последовательно приближаясь от периферии к центру:
1) в области r > R3 величина 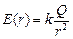 , т.е. функция Е(r) точно такая же, как для поля точечного заряда, поэтому
, т.е. функция Е(r) точно такая же, как для поля точечного заряда, поэтому 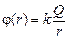 ;
;
2) в области R2 < r < R3 на границах сферического слоя Е(r) изменяется скачком, а поскольку Е(r) = –j¢(r), то функция j(r) в точках r = R3 и r = R3 имеет изломы – скачки производной (1.5,б);
3) поскольку в области 0 < r < R1 величина Е(r) = 0, то j(r) = = const.
СТОП! Решите самостоятельно: А7, В6, В7, С5.
Задача 1.5. Сплошной эбонитовый шар (e = 2,7) радиуса R = = 5,0 см несет заряд, равномерно распределенный с объемной плотностью r = 10 нКл/м3. Определить напряженность в точках, отстоящих от центра шара на расстояниях r1 = 3,0 см и r2 = 20 см. Построить график зависимости Е(r).
| e = 2,7 R = 5,0 см r1 = 3,0 см r2 = 20 см r = 10 нКл/м3 | Решение. Сначала вспомним, как выглядит график Е(r) для равномерно заряженного шара при e = 1. Воспользуемся теоремой Гаусса (рис. 1.6). Рассмотрим поток вектора напряженности через сферу радиуса r > R: | 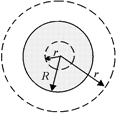 Рис. 1.6
Рис. 1.6
|
| Е(r1) = ? Е(r2) = ? | ||
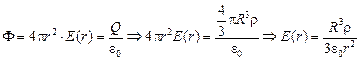 .
.
Теперь рассмотрим поток вектора напряженности через сферу радиуса r < R:
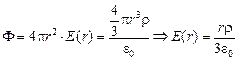 .
.
 Поскольку поле в диэлектрике ослабляется по сравнению с полем в вакууме в e раз, то при 0 < r < R напряженность будет в e раз меньше:
Поскольку поле в диэлектрике ослабляется по сравнению с полем в вакууме в e раз, то при 0 < r < R напряженность будет в e раз меньше:
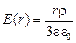 .
.
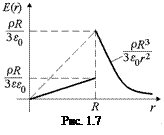
График E(r) показан на рис. 1.7.
Вычислим искомые значения E(r):
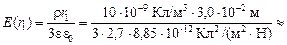 4,2 Н/Кл;
4,2 Н/Кл;
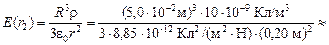 1,2 Н/Кл.
1,2 Н/Кл.
Ответ: 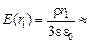 4,2 Н/Кл;
4,2 Н/Кл; 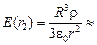 1,2 Н/Кл.
1,2 Н/Кл.
СТОП! Решите самостоятельно: С7, С8.
Дата добавления: 2016-04-11; просмотров: 3447;
