Раздел 3. ЛАБОРАТОРНЫЕ РАБОТЫ
Работа 1. Отдельные электроприемники в цепи однофазного переменного тока
· Цель работы
Исследование цепи однофазного синусоидального тока, состоящей из отдельных электроприемников: резистора, катушки индуктивности и батареи конденсаторов и овладение методикой построения векторных диаграмм.
· Общие сведения
Физические процессы в электрических цепях переменного тока принципиально отличаются от процессов в цепях постоянного тока. Переменные токи и напряжения вызывают появление в некоторых элементах цепи дополнительных ЭДС и токов. Так, переменное магнитное поле вызывает возникновение ЭДС самоиндукции в катушке индуктивности, а изменение электрического поля – токи зарядки и разрядки (токи электрического смещения конденсаторов). Эти ЭДС и токи усложняют расчет цепей переменного тока. Для цепи синусоидального тока большое значение имеет частота f. От частоты зависит влияние индуктивностей и емкостей на их реактивные сопротивления и, следовательно, на процессы в цепи.
Особенности цепей переменного тока обуславливают ряд новых, специфических для этих цепей явлений: сдвиг фаз, явление резонанса, появление реактивных мощностей, их компенсация и др.
При расчете режимов цепей синусоидального тока максимально используются понятия, формулы и методы расчета цепей постоянного тока, изложенные в [1,2]. Это становится возможным благодаря применению описанного в разделе 1.3 комплексного (символического) метода, который в настоящее время является основным при анализе однофазных и трехфазных цепей [1].
В данной работе исследуются процессы, происходящие в цепи однофазного синусоидального тока с отдельно взятым элементом: резистором R (рис. 3.1), индуктивностью L (рис. 3.2) и конденсатором С (рис.3.3).
· Резистивный элемент в цепи синусоидального тока
Резистивный элементили резистор характеризуется активным сопротивлениемR, которое является его параметром и отражает наличие электрического сопротивления проводника переменному току (без учета индуктивности и емкости).
Часто наименование элемента – резистор заменяется наименованием его параметра – активное сопротивление. В активном сопротивлении электрическая энергия необратимо преобразуется в другие виды энергии, в частности, в тепловую энергию, которая рассеивается в окружающее пространство и частично затрачивается на нагревание проводника. Резистивный элемент в схемах замещения может также учитывать потери энергии в магнитопроводе (сердечнике) катушки индуктивности или электрической машины при прохождении через этот сердечник переменного магнитного потока. При промышленной частоте f = 50 Гц активное сопротивление практически не отличается от сопротивления проводника постоянному току.
В цепи синусоидального тока с активным сопротивлением R приложенное напряжение и протекающий ток совпадают по фазе (см. рис. 3.1), то есть угол сдвига фаз между напряжением и током равен нулю:
j = yu - yi = 0
Для участка цепи с активным сопротивлением закон Ома для действующих значений тока и напряжения имеет вид:
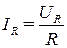 ,(3.1)
,(3.1)
а в комплексной форме:
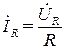 . (3.2а)
. (3.2а)
Отсюда комплексное действующее значение напряжения на резистивном элементе:
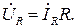 (3.2б)
(3.2б)
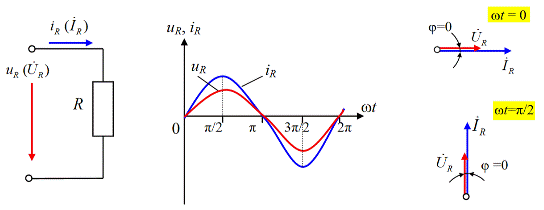
а) б) в)
Рис 3.1. Резистор (R-элемент) в цепи синусоидального тока
а) – эквивалентная схема замещения для резистора R;
б) – графики мгновенных значений напряжения и тока для резистора;
в) – векторная диаграмма действующих значений напряжения и тока для резистора
а) б) в)
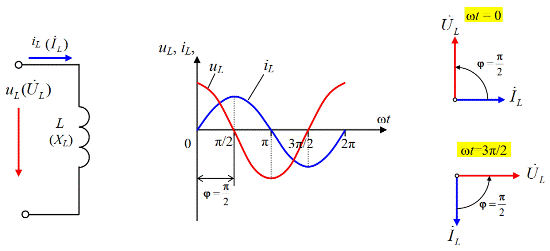
Рис 3.2. Индуктивность (L-элемент) в цепи синусоидального тока
а) – эквивалентная схема замещения для индуктивности L;
б) – графики мгновенных значений напряжения и тока для индуктивности;
в) – векторная диаграмма действующих значений напряжения и тока для индуктивности
а) б) в)
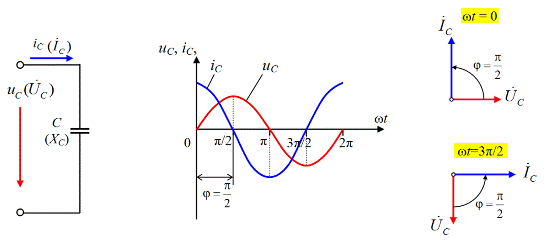
Рис. 3.3. Конденсатор (С-элемент) в цепи синусоидального тока
а) – эквивалентная схема замещения для конденсатора С;
б) – графики мгновенных значений напряжения и тока для конденсатора;
в) – векторная диаграмма действующих значений напряжения и тока для конденсатора
· Катушка индуктивности в цепи синусоидального тока
Катушка индуктивности представляет собой многовитковую катушку, намотанную изолированным проводом с числом витков W.
При протекании через катушку электрического тока внутри и вокруг нее возникает магнитное поле. Сумма магнитных потоков Ф, пронизывающих отдельные витки катушки, то есть сцепленных с ее витками, называется потокосцеплением и обозначается y.
Если все W витков катушки охвачены одним и тем же магнитным потоком, то потокосцепление
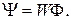
Потокосцепление и ток катушки в линейной цепи прямопропорциональны и связаны соотношением:
Y = Li,
где i – мгновенное значение синусоидального тока; L – коэффициент пропорциональности, называемый индуктивностью катушки.
Единица индуктивности – генри (Гн):
[L] = [Y]/[I] = 1 Вб/А = 1 Всек/A=1 Гн.
Синусоидальный ток, проходящий по катушке индуктивности, помимо активного сопротивления проводников катушки RK , испытывает индуктивное сопротивление XL (Ом). Физически индуктивное сопротивление обусловлено ЭДС самоиндукции е, возникающей в катушке из-за периодического изменения во времени магнитного потока Ф, а, следовательно, и потокосцепления Y[1].
Индуктивное сопротивление прямо пропорционально частоте и индуктивности:
XL = wL = 2pfL, (3.3)
где w =2pf–угловая (циклическая) частота синусоидального тока; f – частота тока, обратная периоду колебаний Т:
f =1/T.
Стандартная промышленная частота в России равна 50 Гц. Единица частоты − герц (Гц):
[ f ]=1/[ T ]= 1/сек =1 Гц.
Единица угловой частоты w – рад/сек.
Из формулы (3.3) следует, что индуктивное сопротивление катушки XL проявляет себя только в цепях переменного тока при f > 0, а в цепях постоянного тока, когда f = 0, XL =0 .
В цепи синусоидального тока с чисто индуктивным элементом (если пренебречь активным сопротивлением проводников катушки индуктивности) ток отстает по фазе от приложенного напряжения на p/2 или 900 (см. рис. 3.2), и, наоборот, можно считать, что напряжение на индуктивном элементе опережает проходящий через него ток на тот же угол j = p/2. То есть угол сдвига фаз между приложенным напряжением и током:
j = yu – yi = p/2, (3.4)
(угол j равен разности начальных фаз напряжения и тока).
Для участка цепи синусоидального тока с индуктивным элементом закон Ома для действующих значений тока и напряжения записывается так:
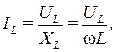 (3.5)
(3.5)
а в комплексной форме:
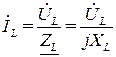 , (3.6)
, (3.6)
где ZL= jXL – комплексное индуктивное сопротивление. (здесь и далее комплексное сопротивление обозначается черточкой внизу для отличия от его модуля); 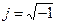 – мнимая единица; XL = wL – модуль (величина) комплексного индуктивного сопротивления.
– мнимая единица; XL = wL – модуль (величина) комплексного индуктивного сопротивления.
Из формулы (3.6) следует, что комплексное действующее напряжение на участке цепи с индуктивным сопротивлением:
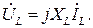
Полное сопротивление ZК катушки индуктивности, которая входит в схему исследуемой цепи с учетом ее активного сопротивления провода RК (см. рис. 3.4), рассчитывается, исходя из закона Ома:
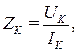 (3.7)
(3.7)
а также по формуле из треугольника сопротивлений [1,2]:
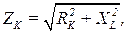 (3.8)
(3.8)
где ZK, Ом – модуль комплексного (полного) сопротивления катушки; RK и XL, Ом – активное и индуктивное сопротивление катушки.
Отсюда индуктивное сопротивление катушки:
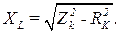
Величина активной составляющей напряжения на катушке:
UR = RK IK.
Реактивная индуктивная составляющая напряжения на катушке:
UL = XL IK.
· Конденсатор (емкостной элемент) в цепи синусоидального тока
Конденсатор представляет собой электротехническое устройство из двух проводников, заряженных разноименными и равными по абсолютной величине зарядами, разделенными тонким слоем диэлектрика. Проводники, образующие конденсатор и имеющие достаточно большую поверхность и малую толщину, называются его обкладками и, как правило, выполняются из алюминиевой фольги.
Конденсаторы служат накопителями зарядов и, следовательно, электрической энергии. Электроемкостьюконденсатора называется физическая величина, равная отношению заряда QC, накопленного в конденсаторе, к напряжению или разности потенциалов UC = j1 – j2 между его обкладками:
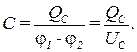
Единица электроемкости называется фарадой (Ф):
[C] = [Q]/[U] = 1 Кл/В = 1 Ф.
Фарада – очень крупная единица емкости, поэтому в практических расчетах применяется в миллион раз меньшая единица – микрофарада (мкФ); 1 мкФ = 10-6 Ф (см. Приложение 1).
Для получения больших электроемкостей конденсаторы соединяют друг с другом параллельно в батарею.
Общая емкость батареи конденсаторов равна:
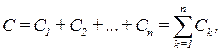
где Сk – емкость k-го конденсатора.
На основании закона Ома для участка цепи с емкостным элементом (с конденсатором) действующее значение тока равно:
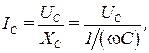 (3.9)
(3.9)
где
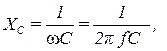 Ом (3.10)
Ом (3.10)
– емкостное сопротивление конденсатора.
Из (3.10) видно, что емкостное сопротивление обратно пропорционально частоте и емкости конденсатора.
Из формул (3.9), (3.10) видно что конденсатор не пропускает постоянный ток (для f = 0 XC = ¥). Если конденсатор подключить к источнику постоянного тока, то в начальный момент в цепи появится только кратковременный зарядный ток. Конденсатор, подключенный к источнику синусоидального напряжения, периодически перезаряжается, и в цепи с конденсатором будет протекать переменный ток той же частоты.
Если емкость С измеряется в микрофарадах, то формула (3.10) имеет вид:
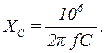 (3.11)
(3.11)
Из формулы (3.9) видно, что размерность емкостного сопротивления – Ом:
[XC] = [UC]/[IC] = 1 B/A = 1 Ом.
Закон Ома для участка цепи с емкостным элементом для комплексов действующих значений тока и напряжения:
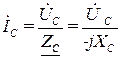 , (3.12)
, (3.12)
где ZC = -jXC – комплексное сопротивление емкостного элемента (конденсатора).
Из формулы (3.12) следует, что комплексное напряжение на конденсаторе равно:
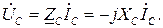 (3.13)
(3.13)
Ток на участке цепи с емкостным элементом при синусоидальном напряжении также синусоидальный и опережает приложенное к конденсатору напряжение на угол p/2 или 900 (см. рис. 3.3,б и рис. 3.3в). Можно сказать, что в этом случае напряжение на конденсаторе отстает по фазе от тока текущего через конденсатор на тот же угол j = p/2.
Таким образом, угол сдвига фаз между напряжением и током с учетом знака равен:
j = yu–yi= –p/2, (3.14)
где yu и yi – начальные фазы синусоидальных напряжения u и тока i, соответственно (см. разд 1.2)
Содержание работы
Лабораторная работа №1 делится на четыре части:
1. Подготовительная часть.
2. Измерительная часть (проведение опытов и снятие показаний приборов).
3. Расчетная часть (определение расчетных величин по формулам).
4. Оформительская часть (построение векторных диаграмм).
Примечание
Электромонтажные работы по исследованию отдельных R,L,C-элементов на модернизированном лабораторном стенде ЭВ-4 [4] с собранной цепью параллельно соединенных электроприемников не проводятся (см. в [2] – Работа 1 п.2. Электромонтажная часть).
1. Подготовительная часть
Подготовка к проведению лабораторной работы включает:
1. Изучение теоретической части настоящего пособия и литературы [1,2,3,4], относящихся к теме данной работы.
2. Предварительное оформление лабораторной работы в соответствии с существующими требованиями [2,3].
В результате предварительного оформления лабораторной работы №1 в рабочей тетради или журнале (на листах формата А4 с компьютерной распечаткой) студентом должен быть заполнен титульный лист, в работе должны быть указаны название работы и ее цель, приведены основные сведения по работе, взятые из раздела выше и формулы, необходимые для вычисления расчетных величин, представлены принципиальные и эквивалентные схемы замещения, заготовлены таблицы, соответственно числу опытов в работе.
Кроме этого, должно быть оставлено свободное место для построения векторных диаграмм.
2. Измерительная часть
Необходимые измерения параметров цепи однофазного тока проводятся с помощью принципиальной схемы (рис. 3.4) при исследовании отдельных электроприемников. Данная схема соответствует панели модернизированного стенда ЭВ-4 [4] с мнемосхемой и цифровыми измерительными приборами для исследования как отдельных, так и параллельно соединенных электроприемников (см .фото на рис. 3.5)
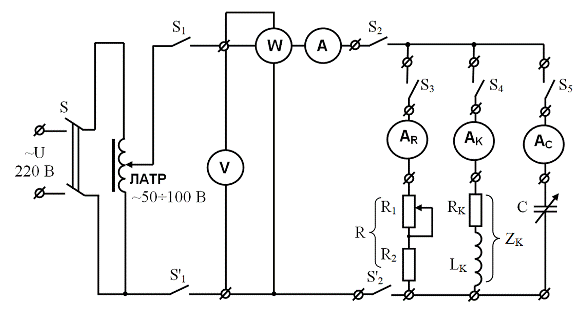
Рис. 3.4. Принципиальная схема цепи синусоидального тока для исследования
отдельных электроприемников
1. Перед подачей питания к исследуемой цепи на панели стенда с мнемосхемой (см. рис. 3.5) перевести все выключатели (S1÷S5, S'1÷S'5) на панели в нижнее положение (состояние – «откл»).

Рис. 3.5. Панель стенда с мнемосхемой и цифровыми измерительными приборами для исследования отдельных электроприемников
2. Лаборант или учебный мастер подключает электронный измерительный прибор – двухлучевой осциллограф С1-55 к зажимам на панели стенда через два экранированных кабеля осциллографа, в соответствии с принципиальной схемой на рис. 3.8, включает осциллограф в сеть и делает начальную регулировку прибора.
3. Подключить лабораторный автотрансформатор (ЛАТР) (см. рис. 3.4), установленный на горизонтальной панели блока питания рис. 3.6) к сетевому напряжению (~220 В) нажатием черных кнопок «вкл» выключателей. При этом загораются две зеленые сигнальные лампы «сеть». После этого нужнообязательноповернуть ручку регулятора ЛАТРАа против часовой стрелки до упора, тем самым, снизив напряжение на его выходедо нуля.

Рис. 3.6. Панель блока питания лабораторного стенда СБ-4
3. Подать регулируемое напряжение от ЛАТРа ко входу исследуемой цепи и подключить цифровые измерительные приборы, установив на панели стенда с мнемосхемой (см. рис. 4.5) кнопки выключателей S1, S'1, S2, S'2 в положение «вкл». При этом должны засветиться зеленые цифры на электроизмерительных приборах.
4. Плавным поворотом по часовой стрелке ручки регулятора ЛАТРа установить напряжение U на входе цепи порядка 50 ÷ 100 В, контролируя его цифровым вольтметром V (прибор ЩП02М, установленный слева на панели стенда – рис. 3.5). Это напряжение остается неизменным для всех трех опытов. При этом ручку регулируемого сопротивления R на панели установить в среднее положение.
5. Установить емкость батареи конденсаторов порядка С » 60 ÷ 100 мкФ нажатием соответствующих черных кнопок выключателей рядом с подключаемыми конденсаторами на панели №4 стенда с мнемосхемой батареи конденсаторов (см. рис. 3.7)

Рис. 3.7. Панель №4 стенда с мнемосхемами батареи конденсаторов
и катушки индуктивности
6. В процессе исследования цепей с отдельными электроприемниками провести три опыта. Для этого следует выполнить следующее:
6.1. В первом опыте – исследование однофазной цепи с активным сопротивлением (R-элемент) подключить к источнику питания (выходу ЛАТРа) резисторы R1, R2 с общим сопротивлением R, включив выключатель S3 (см. рис. 3.4 и рис. 3.5). При этом катушка индуктивности и конденсатор должны быть отключены от питающего напряжения (кнопки выключателей S4 и S5 находятся в нижнем положении «откл»).
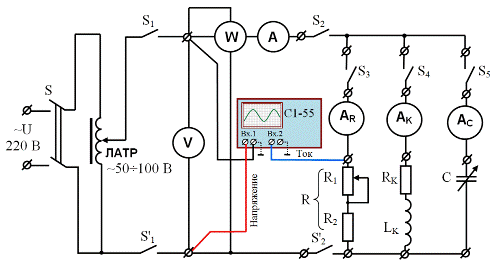
Рис. 3.8. Схема цепи с параллельным соединением электроприемников
при снятии осциллограмм тока и напряжения для активного сопротивления R
6.2. С помощью лаборанта или учебного мастера на осциллографе С1-55 установить нужный тип синхронизации (внутр. I), а также выбрать ручками регуляторов и переключателей по обоим каналам (левый канал I – осциллограмма напряжения, правый канал II – осциллограмма тока) удобные для наблюдения величины усиления (вольт/дел.) и длительности развертки (время/дел.). Кроме того, плавной регулировкой ручками синхронизации и стабилизации (стаб) следует зафиксировать (сделать неподвижными) на экране осциллограммы напряжения и тока
6.3. С помощью двухлучевого осциллографа С1-55 пронаблюдать осциллограммы напряжения и тока в цепи с активным сопротивлением, убедившись, что они совпадают по фазе (см. рис. 3.9).
6.4. Измерить входное напряжение U, потребляемую активную мощность Р и протекающий через активное сопротивление ток IR, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром АR (см. принципиальную схему на рис. 3.4 и панель стенда на рис. 3.5).
6.5. В конце 1-го опыта отключить напряжение питания и активное сопротивление R, установив кнопки выключателей S1, S'1, S2, S'2 и S3 в нижнее положение «откл» (см. рис. 3.5).

Рис. 3.9. Осциллограммы напряжения (кривая 1) и тока (кривая 2)
для цепи с активным сопротивлением
6.6. Во втором опыте – исследование однофазной цепи с индуктивностью (L-элемент) вначале следует подключить катушку индуктивности, обладающую собственной индуктивностью LК с небольшим активным сопротивлением провода катушки (RК = 5 Ом), включив выключатель S4 (см. рис. 3.5 и рис. 3.10). При этом активное сопротивление R и конденсатор C остаются отключенными от питающего напряжения (кнопки выключателей S3 и S5 находятся в нижнем положении «откл»).
6.7. После этого надо подключить конец кабеля осциллографа по каналу II (осциллограмма тока) в гнездо цепи между амперметром АК и резистором RK (см. рис. 3.5 и рис. 3.10).
6.8. Далее нужно подать установленное ранее напряжение U от ЛАТРа ко входу исследуемой цепи (рис. 3.10), установив кнопки выключателей S1, S'1, S2, S'2 в положение «вкл».
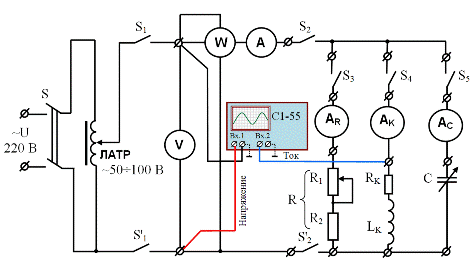
Рис. 3.10. Схема цепи с параллельным соединением электроприемников
при снятии осциллограмм тока и напряжения для катушки индуктивности
6.9. С помощью двухлучевого осциллографа С1-55 пронаблюдать осциллограммы напряжения и тока в цепи с катушкой индуктивности, убедившись, что синусоида напряжения опережает синусоиду тока на четверть периода (т.е. на p/2 или 90о по фазе), как показано на рис. 3.11).
6.10. Измерить входное напряжение U, потребляемую активную мощность Р и протекающий через индуктивность ток IL, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром АK (см. принципиальную схему на рис. 3.10 и панель стенда на рис. 3.5).

Рис. 3.11. Осциллограммы напряжения (кривая 1 – левый канал I)
и тока (кривая 2 – правый канал II)
для цепи с катушкой индуктивности
6.11. В конце 2-го опыта отключить напряжение питания и катушку индуктивности, установив кнопки выключателей S1, S'1, S2, S'2 и S4 в нижнее положение «откл» (см. рис. 33.5 и рис. 3.10).
6.12. В третьем опыте – исследование однофазной цепи с конденсатором (С-элемент) вначале следует подключить конденсатор С, включив выключатель S5 (см. рис. 3.5 и рис. 3.12). При этом активное сопротивление R и индуктивность L остаются отключенными от питающего напряжения (кнопки выключателей S3 и S4 находятся в нижнем положении «откл»).
6.13. Далее нужно подать напряжение от ЛАТРа ко входу исследуемой цепи (рис. 4.12), установив кнопки выключателей S1, S'1, S2, S'2 в положение «вкл».
6.14. С помощью двухлучевого осциллографа С1-55 пронаблюдать осциллограммы напряжения и тока в цепи с конденсатором С, убедившись, что синусоида напряжения (кривая 1) отстает от синусоиды тока (кривая 2) на четверть периода (т.е. на p/2 или 90о по фазе), как показано на рис. 3.13.
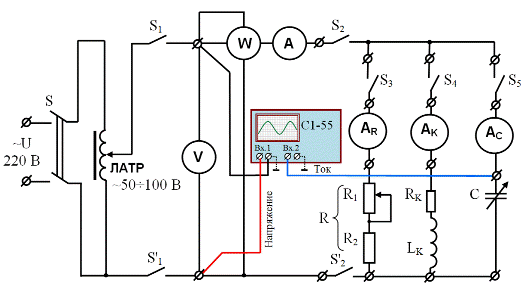
Рис. 3.12. Схема цепи с параллельным соединением электроприемников
при снятии осциллограмм тока и напряжения для конденсатора
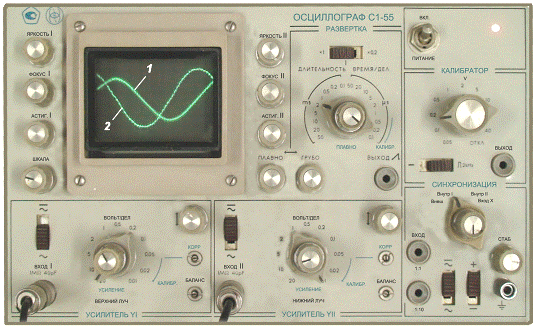
Рис. 3.13. Осциллограммы напряжения (кривая 1) и тока (кривая 2)
для цепи с конденсатором С
6.15. Измерить входное напряжение U, потребляемую активную мощность Р и протекающий через конденсатор ток IС, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром АС (см. принципиальную схему на рис. 3.12 и панель стенда на рис. 3.5).
6.16. В конце 3-го опыта отключить напряжение питания и конденсатор, установив кнопки выключателей S1, S'1, S2, S'2 и S5 в нижнее положение «откл» (см. рис. 3.5 и рис. 3.12).
6.17. После проведения измерительной части работы результаты измерений, относящиеся к данной работе, предъявляются преподавателю или учебному мастеру до отключения стенда и демонтажа цепи.
6.18. Полученные результаты измерений трех опытов заносятся в таблицу 4.1.
6.19. Отключить данную цепь от источника питания и блок питания от силового щитка с помощью выключателей S1 и S1' на панели с мнемосхемой (см. рис. 3.5) и красной кнопки «выкл» выключателя на панели блока питания (см. рис. 3.6). Сообщить преподавателю об окончании измерений и приступить к вычислениям параметров цепи.
3. Расчетная часть
1. По результатам измерений (табл. № 3.1) вычислить активное сопротивление цепи R, величины полного сопротивления катушки индуктивности ZK индуктивного сопротивления XL, емкостного сопротивления конденсатора XC, величины напряжений на активном сопротивлении цепи UR и индуктивном сопротивлении катушки индуктивности UL, а также коэффициенты мощности цепи cosj для всех трех опытов.
Примечание.
Вычисления величин, соответствующие ячейкам с прочерком в табл. 3.1, не проводятся.
2. Вычисления параметров цепи проводить по нижеследующим формулам:
2.1. Величина общего активного сопротивления R для цепи с резисторами R1 и R2 (см. рис. 3.8) определяется через потребляемую активную мощность P1 = Р и ток IR = I в первом опыте:
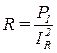 .
.
2.2. Полное сопротивление катушки индуктивности ZK определяется из закона Ома:
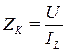 ,
,
где IL = I – ток цепи с катушкой индуктивности во втором опыте.
2.3. Индуктивное сопротивление XL катушки индуктивности определяется из треугольника сопротивлений [1,2]:
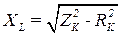 ,
,
где 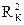 = 5 Ом – активное сопротивление провода катушки индуктивности (см. панель №4 на рис. 3.7).
= 5 Ом – активное сопротивление провода катушки индуктивности (см. панель №4 на рис. 3.7).
2.4. Величина емкостного сопротивления ХС для опыта №3, а также составляющие напряжений UR и UL катушки индуктивности для 2-го опыта определяются из закона Ома для участка цепи:
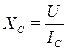 ;
; 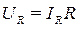 ;
; 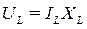 ,
,
где IС = I – ток цепи с конденсатором в третьем опыте.
2.5. Коэффициенты мощности cosφR, cosφL, cosφC, соответственно для 1-го, 2-го и 3-го опыта определяются по следующим формулам:
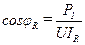 ;
; 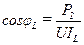 ;
; 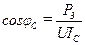 ,
,
где P1, P2, P3 – потребляемые активные мощности Р цепи для 1-го, 2-го и 3-го опыта, соответственно.
Таблица 3.1
Результаты измерений и вычислений для работы 1
| № опыта | Измерено | Вычислено | ||||||||
| U | P | I | R | ZK | XL | XC | UR | UL | cosj | |
| В | Вт | А | Ом | Ом | Ом | Ом | В | В | о.е. | |
| 1. | – | – | – | – | – | |||||
| 2. | – | _ | ||||||||
| 3. | – | – | – | – | – |
Примечания:
Ток I в табл. 3.1 соответствует току IR для 1-го опыта, току IL для 2-го опыта и току IC для 3-го опыта;
4. Оформительская часть – построение векторных диаграмм
1. Перед построением векторных диаграмм внимательно изучить правила их построения, изложенные в разд. 1.4.
2. Выбрать масштабы для напряжений mU и тока mI , как указано в разд. 1.4.
3. С помощью выбранных масштабов определить длины векторов напряжений и тока по формулам:
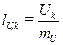 ;
; 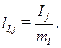
4. Занести выбранные масштабы, измеренные и вычисленные величины напряжений и тока и длины векторов этих величин для трех опытов в табл. 3.2.
Таблица № 3.2
Масштабы, величины и длины векторов напряжения и тока
| № опыта | Масштабы | Базовый вектор | Остальные векторы | |||||||||
| mU | mI | I | lI | UR | lUR | UL | lUL | UC | lUC | U | lU | |
| В/см | А/см | А | см | В | см | В | см | В | см | В | см | |
| 1. | _ | _ | _ | _ | ||||||||
| 2. | _ | _ | ||||||||||
| 3. | _ | _ | _ | _ |
5. Построить для всех трех опытов векторные диаграммы тока и напряжений для отдельных электроприемников R, L, C, пользуясь правилами построения векторных диаграмм, изложенные в разд. 1.4.
Дата добавления: 2016-04-11; просмотров: 3935;
