Понятие о встроенных функциях Маткада.

Большинство задач в Маткаде решаются с помощью так называемых встроенных функций, т.е. с помощью заранее составленных программ решения той или иной задачи. Каждая такая программа имеет свое имя, по которому она вызывается. Имя можно набирать с клавиатуры, но можно и вызывать с помощью кнопки f(x) главного меню. Нажав эту кнопку, мы вызовем панель Insert Function (вставить функцию), в которой имеется два окна: Function Category (тип функции) и Function Name ( имя функции). Выбрав тип и имя, и нажав кнопку ОК, мы вызовем данную функцию (Рис.1).

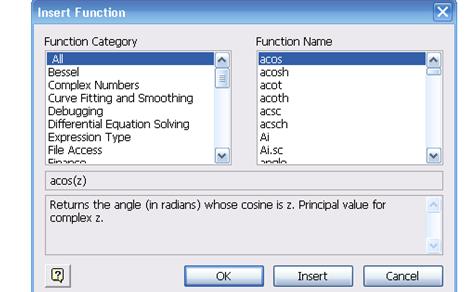
Рис.1.Панель вызова функции

Пусть, например, нужно найти синус числа 45. Вызвав панель вставки функции, выберем категорию Trigonometric и название sin, нажмем ОК. На экране появится шаблон со словом sin внутри и скобками. Вставив в скобки число 45, нажмем «=». Получим sin(45)=0.851. Можно было бы набрать левую часть на клавиатуре и, после нажатия знака =, получить тот же ответ.

Аналогично используются и другие встроенные функции Маткада.

В Маткаде массивы могут записываться в виде векторов (одномерные массивы), в виде матриц (двумерные массивы) и в виде таблиц. Мы рассмотрим пока только запись матриц и векторов. Для действий над ними имеется панель Matrix (матрица), показанная на рис. 2.

Рис.2. Панель матриц

Для ввода матриц и векторов нажмем кнопку панели матриц и вызовем этим окно ввода Insetrt Matrix (ввести матрицу), показанное на рис.3.

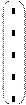
Рис.3. Окно ввода матриц и векторов. Рис.4. Шаблон вектора.

При вводе вектора в графе columns (столбцы) следует проставить 1, а в графе rows(строки) проставить размер вектора. Появится шаблон, показанный на рис. 4.

Ниже представлено три пятиэлементных массива-вектора: Два из них – численные, третий – буквенный, четвертый состоит из выражений.

При задании буквенных массивов и массивов – выражений необходимо предварительно присваивать им численные значения (за каждой буквой в компьютере должно стоять число). После задания выражений вектора можно, записав его имя и поставив знак =, получить его значение. Рисунок лишний раз иллюстрирует, что Маткад различает строчные и заглавные буквы.

Над векторами определены показанные на рис.5.. операции сложения- вычитания, транспонирования, умножения по математическим правилам умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица).

Порядковый номер элемента, который является его адресом, называется индексом.

Нижняя граница индексации задается значением системной переменной ORIGIN, которая может принимать значение 0 или 1.

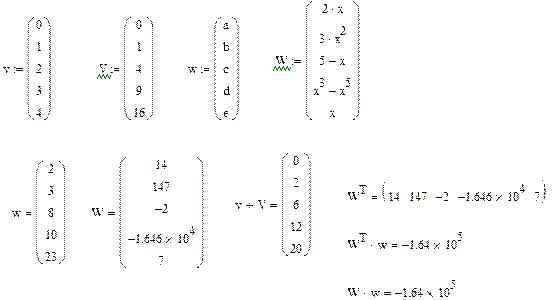
Рис.5. Запись векторов в Маткаде.

Имя массива увязано с именами индексированных переменных, значениями которых являются элементы массива. Для этого достаточно в виде подстрочного индекса указать индекс элемента. Например, если третий из представленных массивов имеет имя V, то его элементами при ORIGIN=0 будут индексированные переменные:

v₀=0 V₁=b ,w₃= d, W₄= x.

При задании ORIGIN=1, получим: v₁ =0, V₁=a, w₃=c, W₄=x³ – x⁵.

Задача 1. Ввести все векторы рис.5 и произвести над ними все действия, проведенные на рисунке. Матрицы в Маткаде вводятся так же, как и векторы, но число столбцов в них – больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рис.6 показаны различные способы ввода матриц.

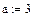
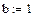
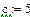
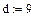
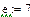
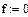
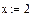
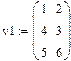
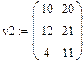
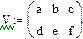
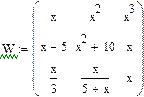
Рис.6. Ввод матриц.

Задача 2.Ввести все матрицы, приведенные на рис.6.

Элементы матриц являются индексированными переменными, имена которых совпадают с именами матриц. Для каждой индексированной переменной указываются два индекса: один - для номера строки, другой - для номера столбца. Например, для матрицы W средний элемент обозначается как W_1,1 а последний как W_2,2. (Индексы набираются через запятую). На рис.7 показано изменение индексации при различных значениях переменной ORIGIN.(Набирается обязательно заглавными буквами).

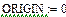
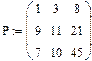
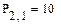
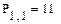
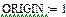
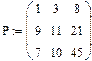
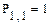
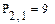
Рис.7. Роль переменной ORIGIN

В Маткаде определены следующие действия над векторами и матрицами:

А) сложение – вычитание,

В) скалярное и векторное умножение,

Г) Обращение,

Д) транспонирование,

Е) Сортировка,

Ж) выделение столбцов.

Они выполняются с использованием следующих кнопок панели Matrix:

кнопка индексации элементов матрицы,

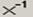кнопка обращения матрицы,

кнопка скалярного произведения векторов и матриц

кнопка транспонирования матрицы,

кнопка векторного произведения двух векторов

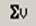кнопка сложения векторов

кнопка выделения столбца матрицы

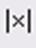
кнопка вычисления детерминанта матрицы.

На рис.8 приведены все эти действия над матрицами, приведенными на рис.6.

Задача.3: Произвести над матрицами все действия, показанные на рис.8..

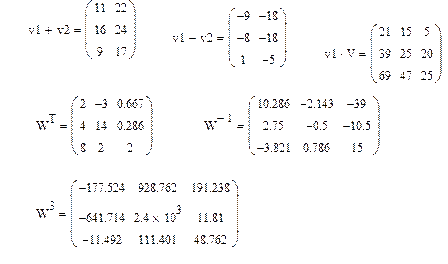
Рис.8. Действия над матрицами

Задача.4: Ввести две произвольные матрицы. Перемножить. Например:

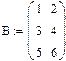
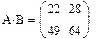
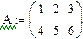
Проверьте на бумаге правильность произведенных выше действий

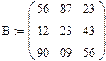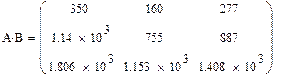
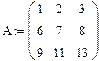
Рис.9. Пример выполнения задачи 4

Обращение и вычисление определителя возможно только для квадратных матриц.

Задача 5.. Введите произвольную квадратную матрицу, найдите обратную ей и вычислите определитель, используя показанные выше кнопки встроенных операторов.

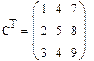
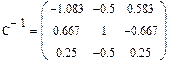
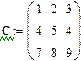
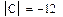
Рис.10. Пример выполнения задачи 5..

Как известно, умножение матрицы на обратную дает единичную матрицу. Проверим, правильно ли было проведено обращение

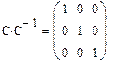
Задача 6. Найти скалярное и векторное произведения двух заданных трехэлементных векторов: Проверить на бумаге правильность вычислений.

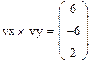
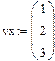
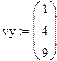
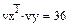
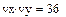
Рис.11.Пример выполнения задачи 6..

. Проверим правильность скалярного умножения, перемножив vx^Т и vy . Получили также 36.

При рассмотрении матриц больших размеров удобно выделять их столбцы. Мы будем использовать его в модулях 2 и 3 при решении сложных задач.

Задача 7. Используя кнопку выделения столбцов, выделите столбцы произвольной матрицы, например:

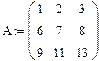
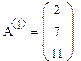
Рис.12.Пример выполнения задачи 7.

В Маткаде имеется большое количество встроенных функций для действий над матрицами и векторами. Рассмотрим некоторые из них.

Вычисление максимального и минимального элементов матрицы или вектора производится с помощью встроенных функций Max(A )и Min(A).

Задача 8. Вычислить максимальный и минимальный элемент произвольной матрицы, например:

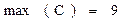
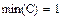
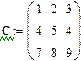
Рис13. Вычисление максимального и минимального элемента матрицы.

Определение количества столбцов и строк в матрице удобно для проверки действий над многомерными матрицами и векторами. Оно производится с помощью встроенных функций Cols(A)- число столбцов матрицы А и Rows(A)-Число строк матрицы А

Задача 9. Определить число строк и столбцов в произвольной матрице, например

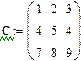
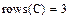
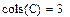
Рис.13. Пример выполнения задачи 9.

Единичная матрица размером N формируется встроенной функцией Idenfity(N),а след матрицы – встроенной функцией .tr(A):

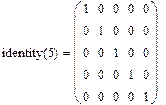
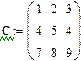
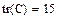
Рис.14. Формирование единичной матрицы и вычисление следа матрицы.