Преобразование случайных величин.

Дискретная случайная величина h принимает значения y₁£ y₂ y₃… y_l с вероятностями P₁, P₂…, P_l составляющими дифференциальное распределение вероятностей:

y y₁ y₂…… y_j…

P(h=y) P₁, P₂……P_j… (3)

При этом интегральная функция распределения y_m£y_m+1; m=1,2,...

F_h(y)=0, y<y₁. (4)

Для получения дискретных случайных величин можно использовать метод обратной функции. Если x - равномерно распределённая на интервале (0, 1), случайная величина h получается с помощью преобразования

h=F_h^-1(x), где F_h^-1 - функция, обратная F_h. (5)

Алгоритм вычисления по (4) и (5) сводится к выполнению следующих действий:

если х₁<Р₁ то h=y₁ иначе,

если х₂<Р₁+Р₂ то h=y₂ иначе,

(6)

если х_j< 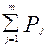то h=y_m иначе

При счёте по (6) среднее число циклов сравнения равняется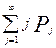

Пример 1. Необходимо методом обратной функции на основании базовой последовательности случайных чисел {x_i}, равномерно распределённых в интервале (0,1), получить последовательность чисел {y_i}, имеющих биноминальное распределение, задающее вероятность у удачных исходов в N реализациях некоторого эксперимента:

P(t_i=y)=P_N(y)=C_N^yP^y(1-P)^N-y , где P=0.5 и N=6; C_N^y=N!/y!(N-y)!

Математическое ожидание и дисперсия биноминального распределения соответственно будут М[y]=np(1-P). Используя для Р_j обозначения, принятые в (6), вычислим:

j …
yj …
Pj …	0.01562	0.09375	0.23438	0.3125	0.23438	0.09375	0.01562
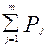…	0.01562	0.10937	0.34375	0.65625	0.89063	0.98438	1.0000

Например, получив из равномерного распределения число Х­_i=0.89063 и проведя сравнения по алгоритму (6), найдём, что 0.85393<0.89063, т.е. y_i=4. При этом среднее число циклов сравнения 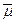=1*0.01562+2*0.09375+3*0.23438+4*0.31250+5*0.23438+6*(0.09375+0.01562)»3.98.