Вычисление непрерывных случайных величин.
Непрерывная случайная величина h задана интегральной функцией распределения:
 , где
, где 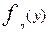 - плотность вероятностей.
- плотность вероятностей.
Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин можно использовать метод обратной функции. Взаимно однозначная монотонная функция h=Fh-1(x), полученная решением относительно h управления Fh(y)=x преобразует равномерно распределённую на интервале (0,1) величину x в h с требуемой плотностью fh(y).
Действительно, если случайная величина h имеет плотность распределения fh(y), то распределение случайной величины 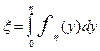 является равномерным.
является равномерным.
Т.о. чтобы получить число, принадлежащее последовательность случайных чисел {y}, имеющих функцию плотности fh(y), необходимо разделить относительно yi управление
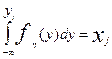 (7)
(7)
Пример 2. Необходимо получить случайные числа yi с показательным законом распределения.
fh(y)=le-ly, y>0.
В силу соотношения (7) получим 
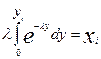 , где xi - случайное число, имеющее равномерное распределение в интервале (0,1), тогда
, где xi - случайное число, имеющее равномерное распределение в интервале (0,1), тогда 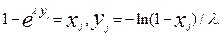
Рассмотрим универсальный метод моделирования непрерывных случайных величин (метод исключений).
При моделировании случайной величины yс плотностью распределения вероятностей fh(y) в интервале a£y£b независимые значения xm и xm+1 преобразуются в значения
y1m=a+(b-a)*xm (8)
z1m+1=f1h(y)* xm+1 (9)
|
где f1h(y)=max| fh(y)|. При этом y1m и z1m+1 - значения случайных величин, равномерно распределенных на интервале (a,b) и (0,f1m). Эти значения можно рассматривать как абсциссы и ординаты случайных точек, равномерно распределяющихся внутри прямоугольника со сторонами b-a и f1m, охватывающего кривую распределения fh(y) (см. рисунок 7.2.).
Рис. 7.2. Иллюстрация метода исключений
Если z1m+1£fh(ym1), (10)
тогда пара y1m, z1m+1 определяет случайную точку под кривой fh. Вероятность попадания случайной точки, удовлетворяющей условию (10) под кривую fh равна единице, а вероятность попадания в заштрихованную элементарную площадку равна fh(y1m)*Dy1m. Это обозначает, что абсциссы y1m случайных точек, попадающих под кривую fh - значения случайной величины y с заданной плотностью вероятности fh(y). Моделируемый алгоритм состоит из функций : 1) получения xm1 и xm+1 от датчика; 2) расчёта y1v и z1m+1 согласно (8) и (9); 3) вычисления fh(y1m); 4) сравнения z1m+1 с fh(y1m). Если условия (10) выполняются, то y=y1m; если нет, то значения y1m и z1m+1 исключаются и процесс повторяется, начиная с пункта 1. При моделировании системы 2-х случайных величин (y1y2) с плотностью вероятности f(y1,y2), a1£y1£b1; a2£y2£b2, аналогично моделированию одной случайной величины, три значения: xm, xm+1, xm+2, выданные датчиком Е, преобразуются в значения:
y1m=a1+(b1-a1)xm (11)
y2m=a2+(b2-a2)xm+1 (12)
z3m=fhmxm+2, где fhm=max[f(x1,x2)] (13)
Если z3m£f(y1m,y2m) (14)
то y1=y1m; y2=y2m.
В этом случае случайные точки с координатами y1m, y2m, z3m - равномерно распределены в пределах параллепипеда со сторонами, равными (b1-a1)(b2-a2), fhm и условие (14) означает попадание точки под поверхность fh. Аналогично моделируется система n случайных величин (y1,y2,…,yn).
6.4 Моделирование нормально распределённой случайной величины y.
Оно может быть осуществлено на основании центральной предельной теоремы, согласно которой закон распределения суммы независимых случайных величин стремится к нормальному с увеличением числа слагаемых. Для решения некоторых задач практически сумму  значений, выданных с генератором случайных чисел с характеристиками f(xi)=1, 0£xi£1, mx=0.5,
значений, выданных с генератором случайных чисел с характеристиками f(xi)=1, 0£xi£1, mx=0.5, 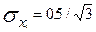 .
.
Можно считать значениями распределённой случайной величины 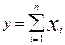 при n³8. Так как все слагаемые xi имеют одинаковые математические ожидания mx и дисперсии Dx, то my=nmx, Dy=nDx. В таблице 1 приведены формулы для расчёта случайных величин для различных видов распределений на базе случайной величины с равномерным распределением.
при n³8. Так как все слагаемые xi имеют одинаковые математические ожидания mx и дисперсии Dx, то my=nmx, Dy=nDx. В таблице 1 приведены формулы для расчёта случайных величин для различных видов распределений на базе случайной величины с равномерным распределением.
Получение случайной величины с различными распределениями.
Таблица 1.
| Нужное распределение | Плотность распределения | Способ получения случайной величины |
| Экспоненциальное | f(y)=le-l(y-m), m£y£¥ | 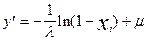
|
| Гамма распределение (целочисленные значения h) | 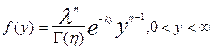
| 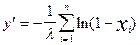
|
| Распределение c2 | 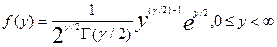
| 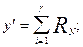 RN - нормированная случ. величина с нормальным законом распределения RN - нормированная случ. величина с нормальным законом распределения
|
| Логарифмические норм. Распределение | 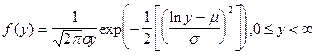
| 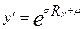
|
| Вейбулла | 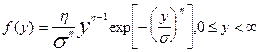
| 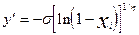
|
Дата добавления: 2016-04-11; просмотров: 972;

