ПИ-закон регулирования
Этот закон получается введением гибкой отрицательной обратной связи по положении регулирующего органа. Гибка связь означает, что в обратную связь включен реальный дифференцирующий элемент, входной сигнал которого максимален в начальный момент времени и исчезает с течением времени. Следовательно, в начальные моменты времени регулятор работает по П-закону, а в конце, когда обратная связь снимается, он работает по И-закону.
Структурная схема ПИ-регулятора такая же, как у П-регулятора, только обратная связь другая – гибкая. При тех же самых основных элементах регулятора: ИУ, ЭС, УУ, ИМ, остается учесть передаточную функцию обратной связи.
Уравнение гибкой обратной связи имеет вид:
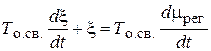 .
.
Отсюда передаточная функция обратной вязи
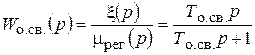 .
.
Получим передаточную функцию регулятора, действуя так же, как и при получении таковой в П-законе.
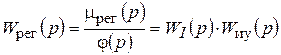 .
.
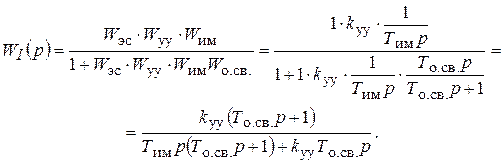
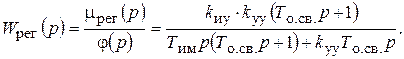
Из последнего соотношения следует уравнение регулятора в операторной форме
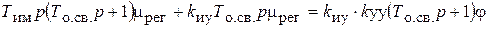 .
.
Отсюда уравнение регулятора
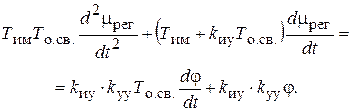 (9.9)
(9.9)
Упростим это уравнение, приняв ТИ.М.®0. Получим
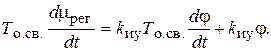 (9.10)
(9.10)
Его решение методом разделения переменных дает
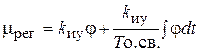 . (9.11)
. (9.11)
Из этого уравнения видно, что перемещение регулирующего органа (mрег) пропорционально регулируемому параметру j и интегралу от него по времени (ПИ-закон).
В литературе это уравнение записывается в виде
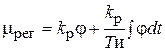 (9.12)
(9.12)
где kр и Ти – параметры настройки ПИ-регулятора (коэффициент усиления и время интегрирования).
Разгонная характеристика ПИ-регулятора имеет вид (рис. 56)
| Рис. 56. Разгонная характеристика ПИ-регулятора |
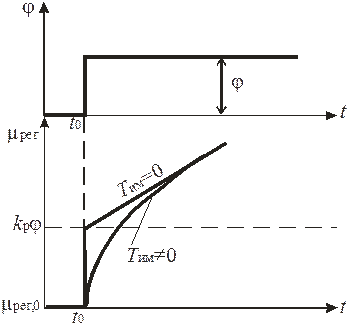
Характеристика, построенная при ТИ.М.=0, соответствует последнему полученному уравнению. Если ТИ.М.¹0, то регулирующий орган будет перемещаться по кривой, которую можно получить из решения дифференциального уравнения второго порядка (9.9).
Такое перемещение регулирующего органа существенно улучшает процесс регулирования по сравнению с И-законом. Это можно увидеть по графику процесса регулирования (рис. 57).
| Рис. 57. Процесс регулирования с ПИ-регулятором |
Из графика видно, что динамическое отклонение параметра А1 меньше, чем у И-закона и время регулирования tр – меньше. К тому же, в статических режимах нет ошибки регулирования, так как среднее значение параметра j в пределах зоны нечувствительности регулятора Dнеч равно заданному значению j0.

| Рис. 57. |
В связи с этими достоинствами ПИ-закон является наиболее употребительным законом при регулировании технологических процессов.
Дата добавления: 2016-04-11; просмотров: 2717;
