СКОЛЬКО МОЛЕКУЛ В ГАЗЕ?
Запишем уравнение Менделеева–Клайперона в виде:
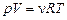 .
.
Здесь n – число молей газа:
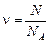 ,
,
где N – число молекул в данном объеме V; NА – число Авогадро. Подставляя значение n в уравнение Менделеева–Клайперона, получим
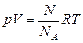 . (17.1)
. (17.1)
Введем обозначение
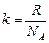 . (17.2)
. (17.2)
Подставим (17.2) в (17.1) и получим
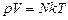 . (17.3)
. (17.3)
Заметим, что коэффициент
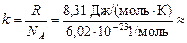 1,38×10–23 Дж/К
1,38×10–23 Дж/К
называется постоянной Больцмана.
Введем величину
п = 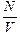 . (17.4)
. (17.4)
Физический смысл этой величины прост – это число молекул в единице объема, [n] = 1/см3. Тогда из (17.3), получим
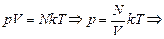
р = nkT. (17.5)
Запомним эту формулу записи уравнения Менделеева–Клайперона. Она нам еще пригодится.
Задача 17.1. Какова концентрация молекул воздуха при нормальных условиях?
| р = 1,013×105 Па Т = 273 К | Решение. Согласно формуле (17.5)
р = nkT Þ
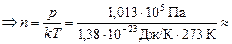 » 2,69×10251/м3.
» 2,69×10251/м3.
|
| п = ? | |
Ответ: п = р/kТ » 2,69×10251/м3.
СТОП! Решите самостоятельно: А3, В1, В2, В7.
Задача 17.2.Найти число молекул в комнате объема V = 100 м3 при температуре Т = 300 К и атмосферном давлении р = 1,013×105 Па.
| V = 100 м3 р = 1,013×105 Па Т = 300 К | Решение. Согласно формуле (17.3)
рV = NkT Þ
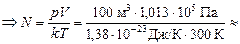 » 2,45×1027 шт.
» 2,45×1027 шт.
|
| N = ? | |
Ответ: 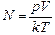 » 2,45×1027 шт.
» 2,45×1027 шт.
СТОП! Решите самостоятельно: А4, А7, В6.
Задача 17.3. Сколько молекул покинет комнату объемом V = =100 м3 при неизменном атмосферном давлении р = 1,013×105 Па и температуре Т = 300 К, если температура в комнате повысится только на 1 К?
| V = 100 м3 р = 1,013×105 Па Т = 300 К DТ = 1 К | Решение. Запишем уравнение Менделеева–Клайперона для обоих состояний:
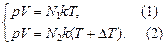 Отсюда
Отсюда
|
| DN = ? |
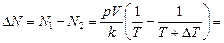
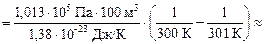 8,13×1024 шт.
8,13×1024 шт.
Ответ: 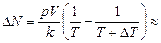 8,13×1024 шт.
8,13×1024 шт.
СТОП! Решите самостоятельно: В8, С1.
Задача 17.4. В сосуде объема V находятся N молекул водорода при температуре Т. Найти давление в сосуде, если: 1) в него добавить N молекул О2; 2) выпустить N молекул образовавшейся смеси.
| V N T m1 m2 | Решение. Сначала давление водорода в сосуде было
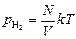 .
Введенный кислород будет иметь парциальное давление .
Введенный кислород будет иметь парциальное давление
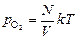 .
По закону Дальтона общее давление составит .
По закону Дальтона общее давление составит
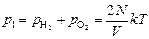 . .
|
| р1 = ? р2 = ? | |
Заметим, что давление зависит не от массы молекул, а только от их числа. После удаления N молекул смеси в баллоне осталось N молекул Н2 и О2. Их давление равно
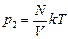 .
.
Ответ: 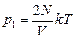 ;
; 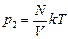 .
.
СТОП! Решите самостоятельно: С13.
Задача 17.5. В сосуде объема 1 л (точно) содержалось т1 = 1 г Н2 и т2 = 1 г О2 (точно) при температуре Т = 273 К. Водород и кислород вступили в химическую реакцию: 2Н2 + О2 = 2Н2О. Определить: 1) сколько получилось молекул воды; 2) сколько осталось молекул кислорода; 3) сколько осталось молекул водорода; 4) давление в сосуде. Температура постоянна. Давлением паров воды пренебречь.
| V = 1 л = 1×10–3 м3 т1 = 1 г т2= 1 г Т = 273 К m1 = 2 г/моль m2 = 32 г/моль | Решение. Определим, сколько молекул Н2 и О2 содержалось в сосуде сначала:
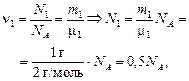
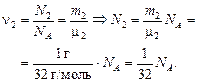
|
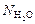 = ? = ?
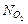 = ? = ?
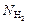 = ? р = ? = ? р = ?
| |
Молекул кислорода в 16 раз меньше, чем молекул воды. Значит, все 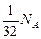 молекул кислорода вступит в реакцию с
молекул кислорода вступит в реакцию с 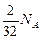 молекулами водорода. При этом образуется
молекулами водорода. При этом образуется 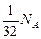 молекул воды и останется молекул водорода
молекул воды и останется молекул водорода
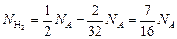 .
.
Давление будет оказывать только оставшийся водород:
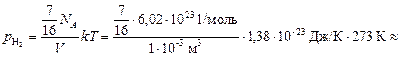
» 9,9×105 Па.
Ответ: 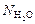 =
= 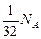 ;
; 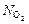 = 0;
= 0; 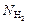 =
= 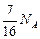 ; р = 9,9×105 Па.
; р = 9,9×105 Па.
СТОП! Решите самостоятельно: В12, С11.
Задача 17.6. В сосуде объемом V = 1,0 л содержится т = 1,0 г гелия (m = 0,004 кг/моль) при температуре Т = 300 К. Определить: 1) среднее расстояние между молекулами; 2) отношение объемов самих молекул к объему сосуда. Молекулы считать шарами с диаметром d » 1,0×10–8 см.
| V = 1,0 л = = 1,0×10–3 м3 т = 1,0 г = = 1,0×10–3 кг m = 0,004 кг/моль Т = 300 К d » 1,0×10–8 см = = 1,0×10–10 м | Решение. Число молекул
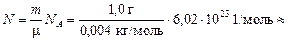 » 1,5×1023 шт.
На одну молекулу приходится объем
» 1,5×1023 шт.
На одну молекулу приходится объем
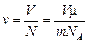 .
Расстояние между молекулами .
Расстояние между молекулами
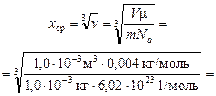 =
= 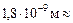 1,8×10–7 см. 1,8×10–7 см.
|
хср = ?
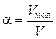 = ? = ?
| |
Заметим, что объем молекулы (шара) равен 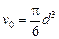 .
.
Отношение объемов молекул и сосуда
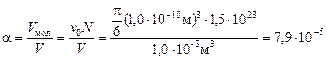 .
.
Ответ: хср » 1,8×10–7 см; 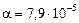 .
.
СТОП! Решите самостоятельно: В11, С3, С12.
Дата добавления: 2016-04-11; просмотров: 1477;
