Холодильная установка
Читатель: Можно ли передать тепло от более холодного тела к более горячему?
Автор: Теплообменом – нет. А вообще – да. Предположим, что у нас есть два одинаковых цилиндра. В одном цилиндре холодный газ, в другом – горячий. Как сделать холодный газ еще холоднее, а горячий – еще горячее?
 Идея.
Идея.
1. Дадим возможность холодному газу, расширяясь, сжать пружину. Газ, совершив работу, еще сильнее охладится (рис. 12.11,а).
2. Дадим возможность пружине, разжимаясь, сжать горячий газ, при этом он станет еще горячее (рис. 12.11,б).
Идея холодильника: тепловая машина обращается вспять!
Пусть имеется тепловая машина с циклом 1–2–1 (рис. 12.12,а), получающая за цикл тепло Q1 у нагревателя, отдающаяся тепло Q2 холодильнику и совершающая положительную работу А > 0 (в координатах р, V процесс идет по часовой стрелке).
а 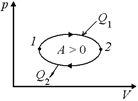 б
б 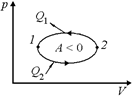
Рис. 12.12
Пустим машину в обратную сторону: сами совершим над рабочим телом работу А > 0 (соответственно, рабочее тело совершит работу (–А) < 0). Заставим рабочее тело забрать теплоту Q2 у холодильника и отдать теплоту Q1 нагревателю (рис. 12.12,б)! Вот вам и периодически работающий холодильник.
Читатель: Как это сделать чисто практически?
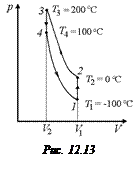
Автор: Рассмотрим следующую схему холодильника (рис. 12.13). Заставим рабочее тело отбирать тепло у воды при 0 °С (и тем самым замораживать её) и отдавать это тепло воде при 100 °С (тем самым превращать ее в пар).
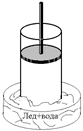
 Возьмем вертикальный цилиндр с поршнем, который можно перемещать вверх–вниз и у которого стенки теплоизолированы, а дно хорошо проводит тепло (рис. 12.14,а).
Возьмем вертикальный цилиндр с поршнем, который можно перемещать вверх–вниз и у которого стенки теплоизолированы, а дно хорошо проводит тепло (рис. 12.14,а).
1. Пусть в начальный момент газ под поршнем находится в объеме V1 при температуре Т1 = –100 °С. Поставим цилиндр в воду со льдом при 0 °С. Вода будет охлаждаться (и замерзать), а газ нагреется до Т2 = 0 °С (рис. 12.14,б) при V1 = const (изохора 1–2 на рис. 12.13).
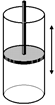
а б в г д
Рис. 12.14
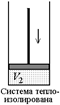
2. Резко сожмем газ (совершив работу) так, чтобы он нагрелся до Т3 = 200 °С (без подвода тепла, адиабатически) (рис. 12.14,в). При этом объем газа уменьшится до V2 < V1 (адиабата 2–3 на рис. 12.13).
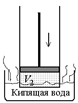
3. Поставим цилиндр в кипящую воду при 100 °С (рис. 12.14,г). Вода будет кипеть и испаряться, а газ – охлаждаться изохорически (V2 = const) до Т4 = 100 °С (изохора 3–4 на рис. 12.13).
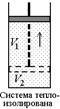
4. Дадим газу адиабатически расшириться до объема V1 так, чтобы температура понизилась до Т1 = –100 °С. Газ вернулся в исходное состояние (адиабата 4–1 на рис. 12.13).
Эффективность холодильной установки определяется холодильным коэффициентом:
| m = | Количество теплоты, взятой у холодильника | |
| Работа, совершенная над рабочим телом |
или
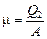 =
= 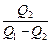 . (12.4)
. (12.4)
где Q1 – теплота, отданная нагревателю; Q2 – теплота, полученная от холодильника; А = Q1 – Q2 – работа, совершенная над рабочим телом.
Задача 12.5. В комнате работает холодильник. За время t он потребляет от электросети энергию W и забирает от охлаждаемых продуктов (и всего остального, что находится внутри него) теплоту Q2. Какую теплоту при этом холодильник передает окружающему воздуху?
| W Q2 | Решение. Пусть Q – общая теплота, полученная рабочим телом холодильника за время t, (U2 – U1) – изменение внутренней энергии рабочего тела. Тогда согласно I началу термодинамики |
| Q1= ? | |
Q = A + (U2 – U1). (1)
Q = Q2 – Q1,
где Q2 – тепло, полученное рабочим телом от охлаждаемых предметов; Q1 – тепло, переданное рабочим телом нагревателю (в конечном счете – воздуху в комнате).
А = –|A| – работа, совершенная рабочим телом, отрицательна: А < 0. Так как работа над рабочим телом совершается за счет электроэнергии, то |A| = W или A = –W.
Так как рабочее тело совершает периодический процесс, постоянно возвращаясь в исходное состояние, то
U2 – U1 = 0.
Тогда из (1) следует
Q2 – Q1 = –W + 0 = –W Þ Q1 = Q2 + W.
Таким образом, нагреватель (воздух в комнате) получит не только тепло, которое рабочее тело отобрало у охлаждаемых продуктов, но и всю электроэнергию, которая тратится на работу холодильника.
Ответ: Q1 = Q2 + W.
СТОП! Решите самостоятельно: А5–А7, В6, С3.
Дата добавления: 2016-04-11; просмотров: 818;
