Практическая конструкция тепловой машины

Возьмем вертикальный цилиндр с плотно подогнанным поршнем, который может фиксироваться в двух положениях: верхнем и нижнем. Под поршнем находится газ. Заставим его совершать полезную работу – поднимать гирю с нижнего уровня на верхний в циклическом режиме (рис. 12.5).

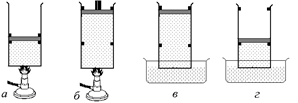
Рис. 12.5

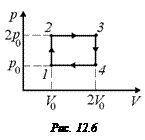1. Пусть в начальный момент газ имеет давление р₀ и объем V₀. Зафиксируем поршень в нижнем положении (рис. 12.5,а)и будем нагревать его пламенем спиртовки изохорически, пока давление не повысится до значения 2р₀ (1–2 на рис. 12.6).

2. Поставим на поршень гирю (ее вес должен быть таков, что mg/S + p_атм £ 2р₀), освободим поршень и будем продолжать нагревать его уже изотермически (т.е. поддерживая давление постоянным) так, чтобы газ расширился до объема 2V₀ (рис. 12.5,б, 2–3 на рис. 12.6).

3. После того как поршень дойдет до верхнего положения, зафиксируем его и снимем гирю (газ уже совершил полезную работу). Теперь надо вернуть его в исходное положение. Для этого поставим цилиндр в холодную воду (рис. 12.5,в) и будем охлаждать рабочее тело изохорически, пока его давление не уменьшится до р₀ (3–4 на рис. 12.6).

4. После того как давление газа понизится до р₀, освободим поршень и будем продолжать охлаждать газ так, чтобы он изобарически сжался до исходного объема V₀ (рис. 12.5,г, 4–1 на рис. 12.6).

Цикл завершен, рабочее тело вернулось в исходное положение.

Задача 12.1. Под поршнем в рассмотренном нами цикле находится одноатомный газ. Значения р₀ и V₀ заданы. Рассчитать КПД цикла.

р0 V0	Решение. 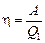. Работу газа вычислим как площадь внутри цикла
h = ?

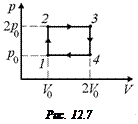А = (2р₀ – р₀)(2V₀ – V₀) = p₀V₀;

Q₁ – полученное тепло.

Заметим, что газ получает тепло на участках 1–2 и 2–3: Q₁ = Q₁₂ + Q₂₃.

Учитывая, что согласно закону Менделеева–Клайперона

nR(T₂ – T₁) = p₂V₂ – p₁V₁,

находим:

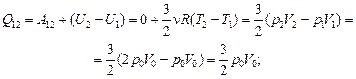
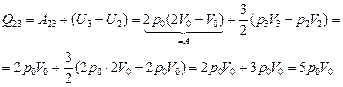
Q₁ = Q₁₂ + Q₂₃ = .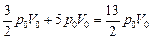

= .

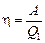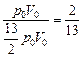Ответ: .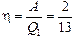

Читатель: А каким бы был КПД нашей тепловой машины, если бы при тех же температурах холодильника (воды) и нагревателя (пламени спиртовки) она была идеальной, т.е. работала по циклу Карно?

Автор: Во-первых, температура холодильника должна быть не выше, чем в точке 1, иначе мы не охладим газ до точки 1. Во-вторых, температура нагревателя должна быть не ниже, чем в точке 3, иначе мы не нагреем газ до точки 3. Запишем уравнение Менделеева–Клайперона для точек 1 и 3:

1: р0V0 = nRTхол, 3: 2 р0 ×2V0 = nRTнагр,

Þ .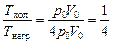

Вычислим КПД по формуле (12.3)

!

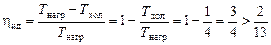СТОП! Решите самостоятельно: С5.

Задача 12.2. Найти КПД тепловой машины, рабочий цикл которой изображен на рис. 12.8. Газ одноатомный, р₀, V₀ заданы.

р0 V0	Решение. 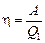, Q1 – то же(!) что и в задаче 12.1, так как газ получает тепло только на участках 1–2 и 2–3. Работа газа за цикл равна площади цикла:
h = ?

.

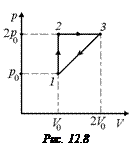
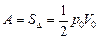Отсюда

.

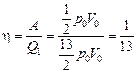Ответ: h = .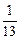

Задача 12.3. Найти КПД тепловой машины, рабочий цикл которой изображен на рис. 12.8. Газ одноатомный, р₀, V₀ заданы.

р0 V0	Решение. Газ получает тепло только на участке 1–2: Q1 = Q12 = А12 + (U2 – U1). А12 – это площадь под графиком на участке 1–2, ее можно вычислить как сумму площади прямоугольника
h = ?
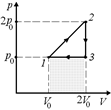Рис. 12.9	р0V0 и треугольника : ; = = ;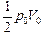

.

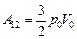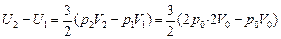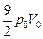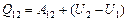
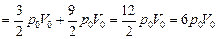Работа газа за цикл – площадь треугольника: 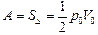, тогда .

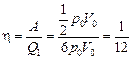Ответ: h = .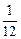

СТОП! Решите самостоятельно: С6.

Задача 12.4. В паровой турбине расходуется 0,35 кг дизельного топлива на 1 кВт×ч. Температура поступающего в турбину пара 250 °С, температура холодильника 30 °С. Вычислить фактический КПД турбины и сравнить его с КПД идеальной тепловой машины, работающей при тех же температурных условиях. Удельная теплота сгорания дизельного топлива q = 42 МДж/кг.

т = 0,35 кг q = 42×106 Дж/кг Т1 = 250 °С = 523 К Т2 = 30 °С = 303 К А = 1 кВт×ч = =1000 Вт×3600 с = = 3,6×106 Дж	Решение. 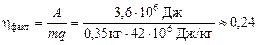, , 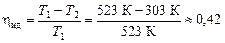hфакт/hид =0,24 : 0,42 » 0,57. Ответ: hфакт/hид » 0,57.
hфакт/hид = ?

СТОП! Решите самостоятельно: А4, В5.