Задач на газовые законы
Задача 8.1. Построить графики изотермического, изобарического и изохорического процессов в координатах (р, V), (V, T), (р, Т).
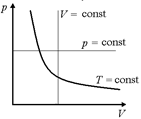 а
а
 б
б
 в
Рис. 8.1
в
Рис. 8.1
| 1. Координаты (р, V) (рис. 8.1,а):
Т = const Þ рV = с Þ p = 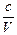 – гипербола;
р = const – прямая, параллельная оси V;
V = const – прямая, параллельная оси р.
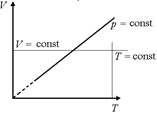
2. Координаты (V, Т) (рис. 8.1,б):
р = const: – гипербола;
р = const – прямая, параллельная оси V;
V = const – прямая, параллельная оси р.
2. Координаты (V, Т) (рис. 8.1,б):
р = const: 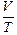 = с Þ V = сТ – прямая, проходящая через начало координат;
V = const – прямая, параллельная оси Т;
Т = const – прямая, параллельная оси V.
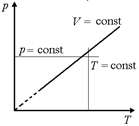
3. Координаты (р, Т) (рис. 8.1,в).
V = const Þ = с Þ V = сТ – прямая, проходящая через начало координат;
V = const – прямая, параллельная оси Т;
Т = const – прямая, параллельная оси V.
3. Координаты (р, Т) (рис. 8.1,в).
V = const Þ 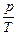 = с Þ р = сТ – прямая, проходящая через начало координат;
р = const – прямая, параллельная оси Т;
Т = const – прямая, параллельная оси р.
Замечание. Вблизи начала координат графики V = сТ и р = сТ следует обозначать пунктирной линией, так как вблизи абсолютного нуля законы = с Þ р = сТ – прямая, проходящая через начало координат;
р = const – прямая, параллельная оси Т;
Т = const – прямая, параллельная оси р.
Замечание. Вблизи начала координат графики V = сТ и р = сТ следует обозначать пунктирной линией, так как вблизи абсолютного нуля законы 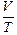 = const и = const и 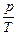 = const не выполняются. = const не выполняются.
|
Задача 8.2. В координатах (р, V) даны две изотермы для одной массы одного и того же газа (рис. 8.2,а). Определить, какая из них соответствует большей температуре.
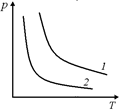
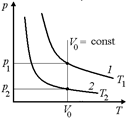
а б
Рис. 8.2
Решение. Для данной массы газа 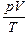 = const. Построим изохору V0 = const для той же массы того же газа. Из графика рис. 8.2,б видно, что р1 > р2. Поскольку согласно уравнению Клайперона
= const. Построим изохору V0 = const для той же массы того же газа. Из графика рис. 8.2,б видно, что р1 > р2. Поскольку согласно уравнению Клайперона 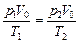 , то
, то 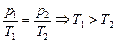 .
.
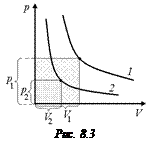 Решим эту задачу другим способом. Возьмем произвольную точку 1 на первой изотерме и произвольную точку 2 на второй изотерме (рис. 8.3). Построим два прямоугольника со сторонами р1, V1 и р2 ,V2. Для состояний р1, V1, Т1 и р2 ,V2, Т2 справедливо уравнение Менделеева–Клайперона
Решим эту задачу другим способом. Возьмем произвольную точку 1 на первой изотерме и произвольную точку 2 на второй изотерме (рис. 8.3). Построим два прямоугольника со сторонами р1, V1 и р2 ,V2. Для состояний р1, V1, Т1 и р2 ,V2, Т2 справедливо уравнение Менделеева–Клайперона
р1V1 = nRT1 и р2V2 = nRT2.
Из графика видим, что площадь первого прямоугольника больше площади второго прямоугольника, значит,
р1V1 > р2V2,
следовательно,
р1V1 = nRT1 > р2V2 = nRT2,
nRT1 >nRT2, Т1 >Т2.
Ответ: Т1 >Т2.
СТОП! Решите самостоятельно: В7, В12, В13.
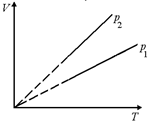
Задача 8.3. В координатах (V, Т) построены две изобары для одной и той же массы газа (рис. 8.4,а). Определить, какая из них соответствует большему давлению.
а б
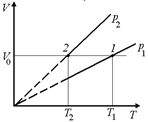
Рис. 8.4
Решение. Возьмем изохору V0 = const для той же массы газа (рис. 8.4,б). Она пересекает изобары в точках 1 и 2, соответствующих температурам Т1 и Т2. Тогда для состояний газа р1, V0, Т1 и р2, V0, Т2 справедливо уравнение Клайперона 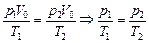 . Так как Т1 > Т2, то р1 > р2.
. Так как Т1 > Т2, то р1 > р2.
Ответ: р1 > р2.
СТОП! Решите самостоятельно: А2, В2, В6, В10.
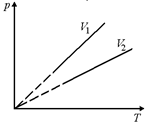
Задача 8.4. На графике в координатах (р, Т) построены две изохоры для одной и той же массы газа (рис. 8.5,а). Определить, какая из них соответствует большему объему.
а б
Рис. 8.5
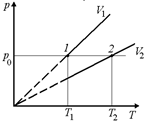
Решение. Строим изобару р0 = const для той же массы газа (рис. 8.5,б). Тогда для состояний газа р0, V1, Т1 и р0,V2, Т2 справедливо уравнение Клайперона 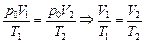 . Так как Т1 < Т2, то V1 < V2.
. Так как Т1 < Т2, то V1 < V2.
Ответ: V1 < V2.
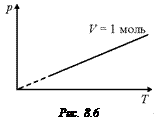 Задача 8.5. На графике в координатах (р, Т) построена изохора для 1 моль газа (рис. 8.6). На том же графике построить изохору для 2 моль газа при том же объеме.
Задача 8.5. На графике в координатах (р, Т) построена изохора для 1 моль газа (рис. 8.6). На том же графике построить изохору для 2 моль газа при том же объеме.
Решение. Согласно закону Менделеева–Клайперона
рV = nRT Þ 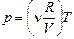 .
.
Введем обозначение 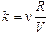 , получим р = kT. Тогда:
, получим р = kT. Тогда:
для 1-го случая р1 = k1T, где k = (1 моль) 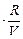 ;
;
для 2-го случая р2 = k2T, где k = (2 моль) 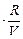 .
.
Отсюда k2 = 2k1. Следовательно, угловой коэффициент второй изотермы, равный тангенсу угла наклона прямой к оси Т в два раза больше, чем у первой. Для построения отметим на первой изохоре точку (Т0, р0) (рис. 8.7), построим точку (Т0, 2р0) и проведем прямую через начало координат и точку (Т0, 2р0).
Рис. 8.7 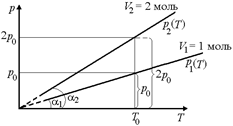
Ответ: см. рис. 8.7.
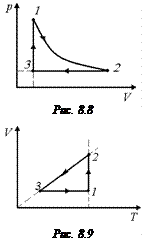 Задача 8.6. На графике в координатах (р, V) построен замкнутый цикл, состоящий из изотермы, изобары и изохоры (рис. 8.8). Построить этот же цикл в координатах (V, Т) и (р, Т).
Задача 8.6. На графике в координатах (р, V) построен замкнутый цикл, состоящий из изотермы, изобары и изохоры (рис. 8.8). Построить этот же цикл в координатах (V, Т) и (р, Т).
Решение. Начнем построение в координатах (V, Т) с процесса 2®3 – это изобара (рис. 8.9). Она изображена прямой, проходящей через начало координат. Проведем эту прямую пунктиром. Поскольку V3<V2, то точка 3 должна находиться на изобаре ниже точки 2. Теперь отметим произвольно точки 2 и 3. Процесс 2®3 изображен.
Процесс 3®1 – это изохора (V = const), причем р1 > р3 (см рис. 8.8). Значит, температура Т на участке 3®1 растет: Т1 > Т3 (см. рис. 8.9). Заметим, что точка 1 должна быть на одной вертикали с точкой 2, так как процесс 1®2 – изотермический (Т = const), причем V2 > V1. Соединив точку 1 с точкой 2, получаем график процесса 1®2.
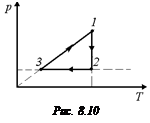 Теперь построим график в координатах (р, Т). Он строится аналогично: сначала изохора 3®1, проходящая через начало координат, потом изотерма 1®2, затем изобара 2®3 (рис. 8.10).
Теперь построим график в координатах (р, Т). Он строится аналогично: сначала изохора 3®1, проходящая через начало координат, потом изотерма 1®2, затем изобара 2®3 (рис. 8.10).
СТОП! Решите самостоятельно: В3, В4, С1.
Задача 8.7. Газ расширяется по закону 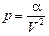 . Как изменяется температура газа? Решить графически.
. Как изменяется температура газа? Решить графически.
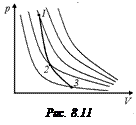 Решение. Проведем в координатах (р, V) несколько изотерм (рис. 8.11). График р = a/V 2 идет круче (убывает быстрее), чем график р = с/V, значит, график р = a/V 2 будет пересекать изотермы.
Решение. Проведем в координатах (р, V) несколько изотерм (рис. 8.11). График р = a/V 2 идет круче (убывает быстрее), чем график р = с/V, значит, график р = a/V 2 будет пересекать изотермы.
Поскольку сверху расположены изотермы с более высокой температурой, а ниже – с более низкой, то Т1 > Т2 >Т3, а значит, с увеличением объема температура понижается.
СТОП! Решите самостоятельно: А3, С3, С7.
Дата добавления: 2016-04-11; просмотров: 2574;
