Элемент электронной схемы ИЛИ-НЕ

Рис. 2.11. Логический элемент электронной схемы ИЛИ-НЕ
Таблица 2.8
Операция ИЛИ-НЕ
| А (вход) | B(вход) | 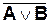 (выход) (выход)
|
2.5 Построение таблиц истинности
для сложных логических выражений
Всякое сложное высказывание, составленное из некоторых исходных высказываний посредством применения логических операций (связок), называют формулой алгебры логики. Если задать значения всех переменных высказываний, то сама формула примет определённое значение. Так как аргументы и функции способны принимать только два различных значения, то такая функция может быть полностью описана конечной таблицей, называемой таблицей истинности.
Построение таблицы истинности позволяет определить истинность сложных логических выражений, заданных в виде формул.
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Этапы построения таблицы истинности.
1. Определить количество наборов входных переменных - всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q = 2ⁿ, где n - количество входных переменных. Оно определяет количество строк таблицы.
2. Внести в таблицу все наборы входных переменных.
3. Определить количество элементарных логических операций и последовательность их выполнения.
4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных (если их более 2-х), можно воспользоваться следующим способом заполнения таблицы.
Способ заполнения таблицы сочетаниями значений входных переменных. Воспользоваться известной таблицей истинности для двух аргументов (4 строки). Добавляя третий аргумент, сначала записать первые 4 строки таблицы, сочетая их со значением третьего аргумента, равным 0, а затем еще раз записать эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк:
| A | B | C |
Для 4-х аргументов повторяем туже операцию, но только уже с восьмью строками. В результате в таблице для четырёх аргументов окажется 16 строк и т.д.
Например: Определить таблицу истинности логической функции:
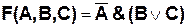
Количество входных переменных в заданном выражении равно трем (А, В, С). Значит, количество входных наборов Q = 23 =8.
Столбцы таблицы истинности соответствуют значениям исходных выражений А, В, С, промежуточных результатов 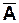 и
и 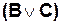 , а также искомого окончательного значения сложного арифметического выражения
, а также искомого окончательного значения сложного арифметического выражения 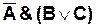 :
:
Таблица 2.9
Таблица истинности функции 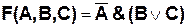
| 
| 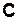
| 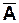
| 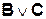
| 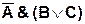
|
Иногда таблицу истинности можно составить более просто, когда каждый аргумент или связка имеют свой столбец.
Например: Вычислить значения функции 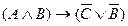 при всевозможных наборах переменных A, B, C.
при всевозможных наборах переменных A, B, C.
Запишем данную формулу в верхнюю строку таблицы и под буквами A, B, C выпишем всевозможные наборы их значений. Затем столбцы под отрицаниями переменных их значениями. Далее заполним столбцы под символами 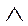 и
и 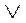 соответственно значениями формул
соответственно значениями формул 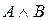 и
и 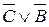 . Наконец, заполним столбец под символом → значениями заданной формулы. В результате получим таблицу 2.10.
. Наконец, заполним столбец под символом → значениями заданной формулы. В результате получим таблицу 2.10.
Таблица 2.10
Таблица истинности функции 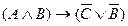
( 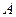
| 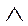
| 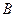 ) )
| ® | ( 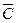
| Ú | 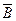 ) )
|
Описанная таблица называется таблицей Куайна. При ее составлении надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться «изнутри наружу», то есть от элементарных формул к более сложным. Столбец, заполняемый последним, содержит значения исходной формулы.
2.6 Основные формулы и законы алгебры логики
Когда мы оцениваем истинность или ложность высказывания, обычно имеем в виду соответствие или несоответствие его содержания действительности. Например, утверждение: «А.С.Пушкин родился в 1799 году» соответствует действительности, и, следовательно, истинно, а утверждение «2+6=9» - ложно.
Однако, для того, чтобы установить истинность или ложность утверждения «треугольник АВС – прямоугольный или косоугольный», вовсе не обязательно измерять углы треугольника. Такое высказывание истинно для любых треугольников, т.к. формула 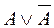 , соответствующая этому предложению, принимает значение «истина» при каждом из значений переменной Х.
, соответствующая этому предложению, принимает значение «истина» при каждом из значений переменной Х.
Формулы, принимающие значение «истина» при всех наборах значений, входящих в них переменных, а также формула «И» называются тавтологиями. Их называют тождественно-истинными формулами. Тавтология играет в логике особо важную роль, как формула, отражающая логическую структуру предложений, истинных в силу одной только этой структуры. Предложения, которые формализуются тавтологиями, называются логически-истинными.
В качестве другого примера рассмотрим формулу 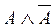 , которой соответствует, например, высказывание «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати». Очевидно, что эта формула ложна, так как либо
, которой соответствует, например, высказывание «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати». Очевидно, что эта формула ложна, так как либо 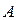 , либо
, либо 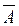 обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями.
обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями.
Противоречие - тождественно ложная формула, или формула принимающая значение "ложь" ("0") при любых входящих в нее значениях переменных.
Логически ложные высказывания - высказывания, которые формализуются противоречиями.
В отличие от табличного задания представление функции формулой не единственно. Будем называть две формулы равносильными, если при любых значениях переменных, входящих в исходные формулы, формулы принимают одинаковые значения. Равносильность двух формул алгебры логики обозначается символами 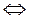 или =.
или =.
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А 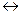 В принимает значение «истина» при любых значениях переменных и обратно, если формула А
В принимает значение «истина» при любых значениях переменных и обратно, если формула А 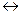 В принимает значение «истина» при любых значениях переменных, то формулы А и В равносильны.
В принимает значение «истина» при любых значениях переменных, то формулы А и В равносильны.
При определении равносильности двух формул не обязательно предполагать, что они содержат одни и те же переменные. Вместе с тем, очевидно, что если какая-либо переменная входит только в одну из равносильных формул, то эта формула при всех значениях этой переменной принимает одно и то же значение. Иными словами, хотя эта переменная входит в формулу, но функция, определённая формулой, от этой переменной не зависит. В тех случаях, когда равносильные формулы равноправны, то есть могут быть заменены одна другой, соотношения равносильности позволяют производить над формулами преобразования, приводящие их к более простому и удобному виду.
Равносильное преобразование формулы - замена формулы другой, ей равносильной.
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные (равносильные) преобразования логических выражений (Таблица 2.11).
Таблица 2.11
Основные законы алгебры логики
| Закон | Для ИЛИ | Для И |
| Переместительный (коммутативности) | 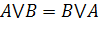
| 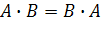
|
| Сочетательный (ассоциативности) | 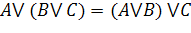
| 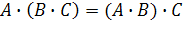
|
| Распределительный (дистрибутивности) | 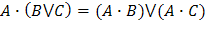
| 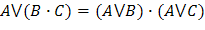
|
| Правила де Моргана | 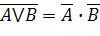
| 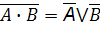
|
| Идемпотентности (отсутствие степеней и коэффициентов) | 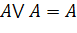
| 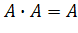
|
| Операция с константами | 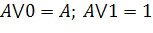
| 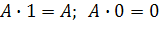
|
| Противоречия (тождественное высказывание) | 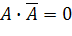
| |
| Исключения третьего (тождественно – истинное высказывание) | 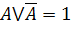
| |
| Двойного отрицания (инволюция) | 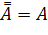
|
Правомерность всех рассмотренных выше законов может быть легко доказана с использованием таблиц истинности.
Как следствие основных законов выводятся формулы (Таблица 2.12), очень полезные при упрощении логических функций.
Таблица № 2.12
Формулы, используемые для упрощения логических функций
| Поглощения | 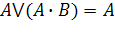
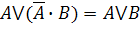
| 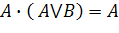
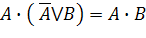
|
| Склеивания | 
| 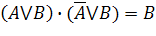
|
| Формулы замены операций | 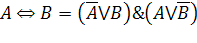
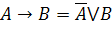
| 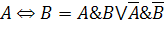
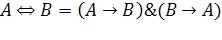
|
Основываясь на законах булевой алгебры, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Если формула составлена только посредством связи конъюнкция (дизъюнкция), то все скобки могут быть опущены. Например, (X&Y)&(X&Y)=X&Y&X&Y.
Сформулируем несколько правил, вытекающих из формул равносильности:
1. Если в логическом произведении один из множителей имеет значение «ложь», то и логическое произведение принимает значение «ложь».
2. Если в логическом произведении, содержащем не менее двух множителей, имеется множитель со значением «истина», то этот множитель можно опустить.
3. Если в логической сумме, содержащей не менее двух слагаемых, имеется слагаемое со значением «ложь», то это слагаемое можно опустить.
4. Если в логической сумме, содержащей не менее двух слагаемых, одно из них имеет значение «истина», то и логическая сумма принимает значение «истина».
5. Очевидно, что если A¢ - подформула формулы A и если заменить любое из её вхождений на эквивалентную формулу B¢, то формула A перейдёт в формулу B, которая будет эквивалентна формуле A. Это правило, называется правилом эквивалентной подстановки.
Логические операции можно выразить через другие на основании формул равносильности. Например,

|
X®Y=ØXÚY
2.7 Чтение электрических схем
Важно уметь читать электрические схемы, т.е. определять их состояние (есть ток или нет тока) в зависимости от состояния контактов при подключенном источнике тока. Так же любую электрическую схему можно разбить на цепочки из последовательно или параллельно соединенных контактов, которые называются элементарными.
Пример 1. Разбить на элементарные цепочки схемы:
a). 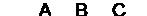 b)
b) 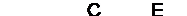
Решение
а) Можно выделить цепи с последовательно соединенными контактами A, B, C и параллельно соединенные цепи (первая - цепь с контактами A, B, C; вторая - цепь с контактом D).
б) Два параллельных соединения В, С и D, E которые объединяются последовательно в одну схему с контактом А.
Пример 2.
Дана схема: 
Состояния контактов задаются таблицей: 0 - контакт разомкнут, 1 - контакт замкнут. Требуется заполнить колонку состояния схемы.
| А | В | С | Состояние схемы |
Первый случай - (0; 1; 1) . Замкнуты контакты В и С, т.е. цепь для прохождения тока создана, состояние схемы- 1. Второй случай - (1; 0; 1), аналогичен первому - ток будет проходить через замкнутые контакты А к С, состояние схемы - 1. Третий случай - (1; 1; 0) , незамкнутый контакт С создает обрыв в цепи. Следовательно, ток протекать не будет, состояние схемы - 0.
| А | В | С | Состояние схемы |
Пример 3. Для предложенной схемы в таблице задано состояние контактов.
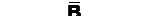 Заполните таблицу.
Заполните таблицу.
| А | В | 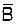
| С | Состояние схемы |
Первый случай - (1; 1; 0; 1). Цепочка замкнутых контактов А, В, С создает путь для тока, состояние схемы - 1. Второй случай - (1; 0; 1; 1). Верхняя цепочка параллельного соединения разорвана, но цепь для тока создается через замкнутый контакт 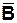 . В цепи будет ток, состояние схемы – 1. Третий случай -(1; 1; 0; 0) . При разомкнутых контактах С и
. В цепи будет ток, состояние схемы – 1. Третий случай -(1; 1; 0; 0) . При разомкнутых контактах С и 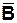 тока в цепи не будет, состояние схемы - 0.
тока в цепи не будет, состояние схемы - 0.
| А | В | 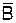
| С | Состояние схемы |
2.8 Составление эквивалентных формул
логических функций и схем
Чтобы изучить свойства переключательной схемы, выявить её возможности и особенности, достаточно рассмотреть соответствующую схеме формулу, которую, если это возможно, упростить. Анализ переключательной схемы позволяет выявить условия, при которых цепь замкнута и позволяет упростить схему с целью уменьшения контактов. О.Б.Лупанов доказал, что любую схему, соответствующую формуле с n переменными можно упростить так, что число контактов в ней не превысит (2n)/n.
Пример 1. Произвести анализ контактной схемы.

При составлении формулы логической функции сначала схему необходимо разбить на элементарные цепочки.
Можно выделить две цепи 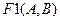 и
и 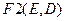 как параллельные и одну общую цепь, состоящую из трёх элементов:
как параллельные и одну общую цепь, состоящую из трёх элементов: 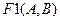 ,
, 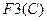 и
и 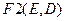 , как последовательную.
, как последовательную.
· последовательные соединения элементарных цепочек представляются как соединение описывающих их функций, связанных логической операцией И
· параллельные соединения элементарных цепочек представляются как соединение описывающих их функций, связанных логической операцией ИЛИ.
Затем для схемы записываются логические формулы каждой из цепочек: 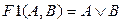 ;
; 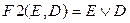
Полученные формулы объединяются логическими операциями ИЛИ и И:
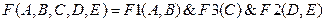
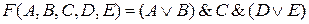
На основе полученной формулы составляется таблица истинности включённого состояния цепи:
| А | В | C | D | E | Состояние схемы |
Пример 2. На основе логической схемы записать функцию и таблицу истинности.

Логическая схема должна иметь три входа 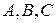 и один выход
и один выход 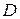 .
.
Начинаем запись функции по элементно.

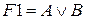 ;
; 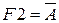 ;
; 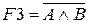 ;
; 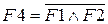 ;
; 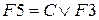 ;
; 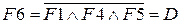
Теперь начинаем подставлять функции в 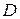 и получаем окончательную функцию:
и получаем окончательную функцию: 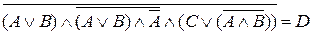
Эту функцию можно упростить, пользуясь законами алгебры логики (Законы де Моргана, коммутативности, идемпотентности, дистрибутивности, двойного отрицания, исключения третьего и т.д.).
Упрощать функцию будем по действиям. Распишем эти действия.
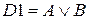
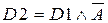
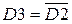
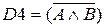
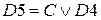
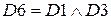
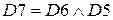
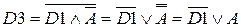 (первый закон де Моргана и инволюции)
(первый закон де Моргана и инволюции)
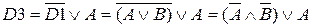 (второй закон де Моргана)
(второй закон де Моргана)
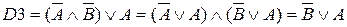 ( закон дистрибутивности и закон исключения третьего)
( закон дистрибутивности и закон исключения третьего)
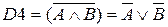 (первый закон де Моргана)
(первый закон де Моргана)
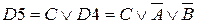
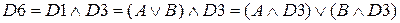 (закон дистрибутивности)
(закон дистрибутивности)
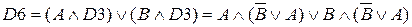
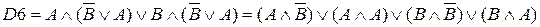 (дистри-бутивности)
(дистри-бутивности)
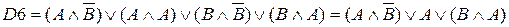 (закон идемпотентности и противоречия)
(закон идемпотентности и противоречия)
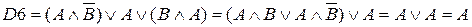 (закон склеивания и идемпотентности)
(закон склеивания и идемпотентности)
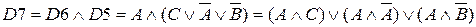 ( закон дистрибутивности, закон противоречия)
( закон дистрибутивности, закон противоречия)
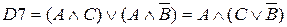 (дистрибутивности)
(дистрибутивности)
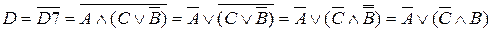
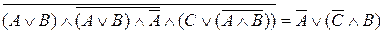
| A | B | C | F1 | F2 | F3 | F4 | F5 | F6 | 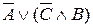
|
2.9 Типовые комбинационные схемы
В состав процессора входит арифметико-логическое устройство (АЛУ), позволяющее выполнять различные арифметические и логические операции на компьютере. АЛУ состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры[9], полусумматоры[10], сумматоры[11], дешифраторы [12]шифраторы[13], регистры[14].
Триггеры обычно имеют 2 выхода: прямой Q и инверсный  . В единичном состоянии на выходе Q сохраняется высокий уровень напряжения, в нулевом - низкий, на выходе - наоборот.
. В единичном состоянии на выходе Q сохраняется высокий уровень напряжения, в нулевом - низкий, на выходе - наоборот.
Для управляющих входов триггера приняты следующие обозначения:
· S (Set - установка) - вход для раздельной установки триггера в состояние логической 1 ( 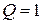 ;
;  ).
).
· R (Reset - сброс) - вход для раздельной установки триггера в состояние логического 0.
· T (Toggle - релаксатор) - счетный вход триггера.
· J (Jerk - внезапное включение) - вход для раздельной установки в логическую 1 универсального JK-триггера.
· K (Kill - внезапное отключение) - вход для раздельной установки в логический 0 универсального JK-триггера.
· D (Delay - задержка, Drive - передача) - информационный вход для установки триггера в 0 или в 1.
· V (Valve - клапан, вентиль) - управляющий вход для разрешения приема либо информационных, либо тактовых сигналов.
· C (Clock - сигнал синхронизации) - тактовый вход, разрешающий схеме управления запись информации в триггер.
Существуют разные варианты исполнения триггеров в зависимости от элементной базы (И-НЕ, ИЛИ-НЕ) и функциональных связей между сигналами на входах и выходах (RS, JK, Т, D и другие). На следующих рисунках приведены примеры различных триггеров.
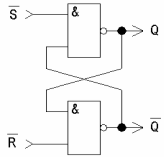
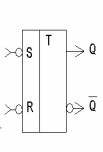
Рис. 2.12 RS-триггер на логических элементах И-НЕ
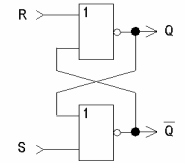
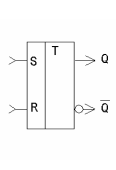
Рис. 2.13 RS-триггер на логических элементах ИЛИ-НЕ
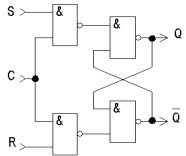
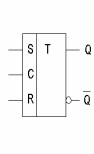
Рис. 2.14 Схема тактируемого RS-триггера
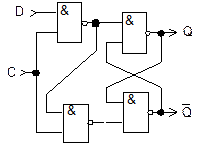
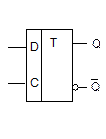
Рис.2.15. Схема D-триггера
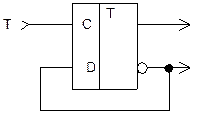
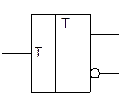
Рис. 2.16. Схема T-триггера
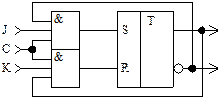
Рис. 2.17. Универсальный JK – триггер
Принципиальная схема полусумматора на базе простейших логических элементов можно представить в следующем виде:

Рис. 2.18 Электронная схема полусумматора

Рис. 2.19. Условное обозначение полусумматора
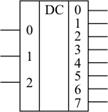
Рис. 2.20 Условное обозначение дешифратора
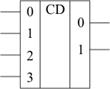
Рис. 2.21 Условное обозначение шифратора
2.10 Упражнения ко второй главе
1) Каждое из следующих предложений замените конъюнкцией или дизъюнкцией, имеющей тот же смысл:
«Число а принадлежит хотя бы одному из множеств А или В».
«Числа a и b имеют разные знаки».
«Три точки A, B, C лежат на одной окружности».
2) Пусть A – «Сегодня ясно», B – «Сегодня дождь», C – «Сейчас идет снег», D – «Вчера было пасмурно». Прочитайте следующие предложения:
| A®Ø(B Ú C); | D ® B Ú A; |
| (D ® A) & (A ® D); | (B Ú C) ® ØA; |
| A º Ø(B & C). |
3) По мишени произведено 3 выстрела. Пусть Ak – «мишень поражена при k-ом выстреле», k=1,2,3. Запишите на языке логики высказываний, следующие предложения:
«Есть хотя бы одно попадание».
«Мишень поражена трижды».
«Нет ни одного попадания».
«Только один выстрел попал в цель».
«Хотя бы два выстрела поразили цель».
4) Сформулируйте отрицания для следующих предложений, укажите значения (истина или ложь) данных высказываний и их отрицаний.
«Луна - спутник Сатурна».
«5 является решением уравнения x2-3x+2=0».
«Среднее арифметическое x и y меньше их среднего геометрического».
«Александр Македонский жил в прошлом веке».
«Параллельные прямые пересекаются».
5) Составить таблицы истинности для следующих формул. Проверить является ли указанная формула тавтологией:
ØC & B Ú ØC & A º (B Ú ØC);
(x1 ® x2) Å (Øx3 & x2);
(x ® y) & (y ® x);
((x Ú y) & (z Ú Øx)) Ú Øz º (x Ú y);
(x Ú y Ú z) º (x & y & z).
6) Рассмотрим высказывания: А – «этот четырёхугольник параллелограмм»; В – «этот четырёхугольник ромб». Прочитайте словесно формулы. Какие из них по содержанию истинны независимо от значений истинности A и B:
| ØА; | А & ØВ; | А ® В; |
| В ® А; | ØА ® ØВ; | ØВ ® ØА. |
7) Составить таблицы истинности.
(x Ú y) ® (Øx & (Øy Ú z));
((x ® Øx) Ú y) º (Øz Ú (Øy & z));
(x & y) Ú (Øx ® (Øy º z));
((x & y) & z) ® ((x Ú y) Ú z);
((x ® y) Å Øx) º (Øy Ú (x & z)).
8) Докажите или опровергните логическую истинность предложений:
«Неверно, что n- простое или сложное тогда и только тогда, когда это число не простое и не сложное».
«Если a=0 или b=0, то a¹0 или b¹0».
«Прямые а и в на плоскости параллельны или пересекаются».
«Если три прямые попарно пересекаются, то они имеют общую точку».
«Если последовательность ограничена, то она имеет предельную точку».
9) Упростить с помощью равносильных формул следующие функции. Составьте для полученных функций таблицы истинности:
F = Ø(Ø x1 ® x2) & Ø(Øx2 Ú x1);
F = Ø(x ® y) & ((y Ú z) Ú Øx);
F = Ø(Øx & y) ®Ø(x Ú z);
F = Ø(x Å z) ® ((x & y) º (x & y));
F = Ø(x º z) ÚØ(Øx & y).
10) Какие из данных формул равносильны:
| ØХ Ú ØY; | ØХ & ØY; | Ø(Х Ú Y); | Ø(Х & Y). |
11) По законам де Моргана переформулируйте следующие предложения:
«Неверно, что треугольник ABC прямоугольный и равнобедренный»
«Неверно, что число g чётное или простое»
«Неверно, что хотя бы одно из чисел Х1, и Х2 – простое»
12) Применяя законы дистрибутивности & и Ú относительно друг друга, составить, равносильные данным, предложения:
«Он знает программирование и алгебру или геометрию».
«Я куплю товар и перепродам его или не буду покупать».
«Число n делится на 2 или на 3 и делится на 2 или на 5».
13) Составьте формулы логических функций соответствующих ниже приведённым логическим схемам и постройте таблицы истинности.


14) Составьте формулы логической функции, соответствующих ниже приведённым электрическим схемам, и постройте таблицы истинности



3.
[1] Язык – это знаковая система, выполняющая функцию формирования, хранения и передачи информации в процессе познания действительности и общения между людьми.
[2] Логика – наука, изучающая с формальной точки зрения понятия, методы их определения и преобразования, суждения о них и структуры доказательных рассуждений.
[3] Алгебра логики - это раздел математики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
[4] Булева алгебра - раздел математической логики, изучающий высказывания и операции над ними. Название получила в честь англ. математика и логика Джорджа Буля (1815-1864).
[5] Переключательная схема - это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. Электрический переключатель либо пропускает ток, что соответствует значению 1 - Истина, либо не пропускает, что соответствует значению 0 – Ложь.
[6] Логический элемент - это схема, реализующая логические операции И, ИЛИ, НЕ.
[7] Таблица истинности - это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
[8] Электромагнитное реле - электрическое устройство, с помощью которого первая электрическая цепь управляет второй.
[9] Триггер – электронная схема, обладающая двумя устойчивыми состояниями. Переход из одного устойчивого состояния в другое происходит скачкообразно под воздействием управляющих сигналов. Одному из этих состояний приписывается значение логической 1, а другому - логического 0. Под влиянием входного импульса триггер скачкообразно переходит из одного состояния в другое, после чего он сохраняет новое состояние неограниченно долго.
[10] Полусумматором называется комбинационная схема с двумя входами и двумя выходами, на которых вырабатываются сигнал суммы и переноса согласно правилам двоичной арифметики.
[11] Сумматор - это устройство (регистр АЛУ), предназначенное для суммирования двоичных кодов, строится как логическая схема на основе одноразрядных двоичных сумматоров.
[12] Дешифратором называется комбинационная схема, преобразующая двоичный код, подаваемый на входы, в сигнал на одном из выходов
[13] Шифратором называется комбинационная схема, преобразующая унарный код (один из Nn) в двоичный код, т.е. выполняют операцию, обратную операции дешифраторов. Одно из основных применений шифратора - это ввод данных с клавиатуры, при котором нажатие произвольной цифровой клавиши должно приводить к передаче в устройство соответствующего данной цифре двоичного кода
[14] Регистром называется устройство, предназначенное для запоминания двоичных слов, а также для выполнения над словами некоторых логических операций.
Дата добавления: 2016-04-11; просмотров: 1510;
