Рупорные ГГ, устройство, назначение рупора и предрупорной камеры, преимущества и недостатки. Основные условия равномерности ЧХ мощности542

Эффективность громкоговорителей прямого излучения из-за малой величины г_из чрезвычайно низка (в лучшем слу­чае КПД не превышает не­скольких процентов, а ча­сто — долей процента). Если головку прямого излучения нагрузить рупором (рис. 1.6,а), то в области низких частот (ka<1, a — радиус основания диафрагмы) из­лучаемая ею акустическая мощность возрастет в 4π/k²а² раз (n=S/S₀, S и S_o — соответственно площади ос­нования диафрагмы и горла рупора, k = ω/c₀). Такая ру­порная система, в которой S₀ мало отличается от S и n~1, называется широкогорлой. Указанное повыше­ние эффективности головки будет иметь место лишь втом случае, если в вы­бранном рупоре обеспечивается: а) активный характер входного сопротивления и независимость его от частоты; б) отсутствие отражения от выходного отверстия.

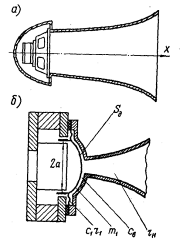
Рис.1.6. Рупорные громкоговорители:

а-широкогорлый;

б-нормальный(узкогорлый);

Наибольшее распространение в практике получили ру­поры, сечение которых изменяется с расстоянием по экспо­ненциальному закону

S = S_oe^2δx,(1.27)

где δ — коэффициент расширения рупора, х — расстояние, отсчитываемое вдоль оси рупора от начального сечения S₀его горла.

Такой рупор называется экспоненциальным и при беско­нечной длине его входное сопротивление z_BX выражается соотношением

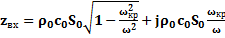(1.28)

Графики активной и реактивной составляющих z_BX, нор­мированные по 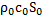, представлены в зависимости от безраз­мерной частоты ν= 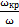на рис. 1. 7. Из формулы (1.28) и рис. 1.7 видно, что на частоте 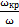=1, называемой критической частотой рупора, активная составляющая г_вх входного сопротивления исчезает, и излучение теоретически должно прекратиться. Первое из поставленных выше требо­ваний ( 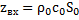) приближенно удовлетворяется в области 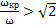, когда активная составляющая 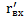начинает преоб­ладать над реактивной. Таким образом, критиче­ская частота рупора определяет нижнюю границу его paботы. Она зависит от коэффициента расширения рупора

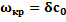(1.29)

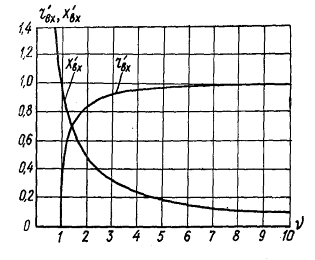
Рис. 1.7. Частотная зависимость норми­рованных значений активной (г'_вх) и ре­активной (х'_вх) составляющих входного сопротивления бесконечного экспоненци­ального рупора

Как видим, для снижения 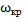нужно уменьшать коэффи­циент расширения, однако это вступает в противоречие со вторым требованием, сформулированным выше, как условие отсутствия отражения от выходного отверстия. В реальных условиях рупор имеет ограниченную длину l, определяющую площадь его выходного отверстия

S_l = S_oe^2δl (1.30)

от диаметра которого зависит сопротивление излучения отверстия z_t = r_i+jx_i во внешнюю среду. Если волновой размер выходного сечения рупора мал, то от этого сечения происходит отражение звуковой волны. Интерференция внутри рупора отраженной волны с прямой обуславливает резонансные неравномерности обеих составляющих входного сопротивления. В частности, активная составляющая г_вх рупора конечных размеров выра­зится соотношением

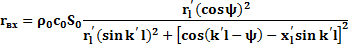
(1.31)

где k'= 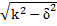, 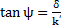нормирован­ные no 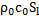значения активной и реактивной компонент сопротивления излучения выходного отверстия.

Чем короче рупор и меньше S_l, тем резче выступают интерференционные неравномерности г_вх и х_вх (рис. 1.8). К такому же результату, при заданной длине l, приводит уменьшение коэффициента расширения δ (или снижения критической частоты).

Кроме экспоненциального, существует еще большое число разновидностей рупоров, отличающихся законами измене­ния сечения с расстоянием. Среди них следует отметить семейство рупоров Бесселя, форма которых выражается степенными функциями вида

S = S₀(l + a_nx)ⁿ, (1.32)

где n —целое число, выражающее степень функции, a_n— коэффициент, вычисляемый по формуле

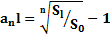
В частности, при n=1 получается параболический, а при n = 2— конический рупоры (рис. 1.9,а,б). Можно показать, что при n 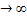степенной рупор превращается в экспо­ненциальный. Функция

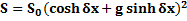(1.33)

определяет другое семейство рупоров, называемых гипербо­лическими. В этой формуле величины δ и g называются соответственно коэффициентами расширения и формы ру­пора. При g=1 получаем экспоненциальный рупор

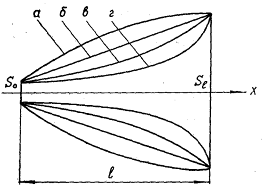
Рис. 1.9. Различные формы рупоров:

а — параболическая; б — коническая; в — экспоненци­альная; г — катеноидальная

(который таким образом является как бы граничным между семействами бесселевых и гиперболических рупоров), а при g = 0 — катеноидальный (рис. 1.9, в, г).

Активная г_вх и реактивная х_вх компоненты входного со­противления гиперболического

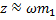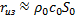В широкогорлых рупорах используются обычные головки прямого излучения, подвижная система которых в рабочем диапазоне частот управляется массой подвижной системы m₁. Поэтому, приняв , а , видим, что КПД широкогорлого рупорного громкоговорителя с повышением частоты уменьшается. Однако, вследствие больших волновых размеров выходного отверстия, одновре­менно с понижением КПД происходит обострение направленности и увеличение коэффициента Ω осевой концентрации излучения. Поэтому осевая интенсивность и звуковое давление с частотой почти не изменяются, пока на высоких частотах система не превращается в обычный громкоговоритель прямого излучения.

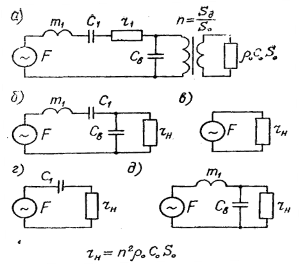
Рис. 1.11.Эквивалентные электрические схемы нормального рупорного громкого­ворителя:

а — полная; б — упрощенная (приведенная к пло­щади диафрагмы);

в — для средних; г — для низ­ких; д — для высоких частот

Другой тип рупорного громкоговорителя, на­зываемый узкогорлым или нормальным (см. рис. 1.6,б), состоит из рупора с очень малой площадью входного отвер­стия S₀ и специальной рупорной головки, имеющей легкую куполообразную диафрагму с площадью S_Д. Щелевидная полость между диафрагмой и входным отверстием рупора образует так называемую предрупорную камеру, которая бла­годаря сравнительно большому значению коэффициента трансформаций n=S_д/S₀ существенно увеличивает полезное сопротивление, нагружающее диафрагму. Полная эквива­лентная схема акустико-механической системы нормального рупорного громкоговорителя представлена на рис. 1.11,а. Здесь m₁=m_k+m_д (m_к — масса звуковой катушки, m_д — диа­фрагмы) ; с₁ и r₁— гибкость и внутреннее трение гофриро­ванного воротника, являющегося подвесом подвижной си­стемы. Нагрузка трансформатора на этой схеме, строго говоря, должна быть представлена комплексным входным сопротивлением рупора конечной длины. На рис. 1.11,а это сопротивление принято равным 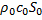, что допустимо, если отражение от выходного отверстия рупора мало и ω> 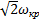. При разумных размерах рупора эти требо­вания удается выполнить только для сравнительно высокой критической частоты (f_Kp = 400—500 Гц). Поэтому нор­мальные рупорные громкоговорители предназначаются преимущественно для работы в средне- и высокочастотных звеньях громкоговорящих систем.

Куполообразные диафрагмы изготавливаются, как пра­вило, совместно с гофрированным воротником из металличе­ской фольги (обычно алюминиевой) или полимерных мате­риалов. Коэффициент механических потерь такой диафрагмы не велик, поэтому величиной внутреннего трения (см. рис. 1.11, а) можно пренебречь. Тогда эквивалентная схема примет вид, представленный на рис. 1.11,6. На частоте ме­ханического резонанса подвижной системы диафрагма нагружена практически лишь сопротивлением r_н (рис. 1.11, в), а в области низких частот величина и характер частотной зависимости механического сопротивле­ния подвижной системы определяется гибкостью диафрагмы (рис.1.11,г). На высоких частотах эквивалентная схема имеет вид Г-образного звена несимметричного фильтра низкой частоты (рис. 1.11,д).