Объем воздуха в помещении как трехмерная колебательная система. Волновое уравнение и его решение

по волновой теории воздушный объем помещения представляет собой трехмерную колебательную систему с распр. параметрами. такая система обладает определенным спектром собственных частот и соответствующими постоянными затухания, характеризующими энергию и скорость затухания каждого из собственных колебаний.

при воздействии сигнала источника в воздушном объеме помещения возбуждаются собственные колебания с частотами, близкими к частотам спектральных составляющих сигнала. спектр возбужденных колебаний зависит не только от спектра сигнала, но и от положения источника в помещении. после выключения источника или в паузах сигнала каждое собственное колебание затухает со своей скоростью, образуя по совокупности с другими собственными колебаниями интерференционную картину постепенно затухающего отзвука или реверберации.

волновое уравнение:

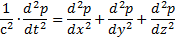
Для определения частот собственных колебаний замкнутого воздушного объема рассмотрим некоторые помещения в форме прямоугольного параллелепипеда с гладкими поверхностями. центр (начало) прямоугольной системы координат 0 совмещен с одним из углов на полу помещения, так что ось х располагается по длине, ось y – ширине, ось z – высоте помещения.

решение трехмерного уравнения при граничных условиях, определяющих жесткость стен помещения, имеет вид

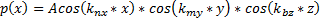
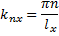
остальные аналогично.

полученное решение определяет распределение звукового давления стоячих волн в пространстве помещения. закон распределения звукового давления в пространстве называется модой колебания. каждому распределению давления соответствует своя частота колебаний, называемая собственной частотой колебаний.

собственные частоты колебаний прямоугольного помещения с жесткими стенками определяют по формуле

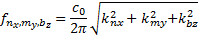
звуковое поле в помещении представляет собой композицию стоячих волн, форма которых определяется собственными функциями колебаний.

если линейные размеры помещения совпадают, то это приводит к уменьшению собственных частот – вырождение собственных частот. при увеличении номера моды, значения собственных частот все более плотно укладываются в третьоктавный диапазон.

выше 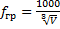, бессмысленно рассчитывать собственные частоты – волновая теория не описывает звуковое поле.

Дюамель вывел выражение для собственного периода 1/fo объемного резонатора в форме прямоугольного параллелепипеда, в котором длина волны

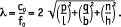
Отсюда

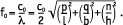
В приведенных выражениях l, b, h – линейные размеры, р, q, n – любые целые числа. В зависимости от значений коэффициентов р, q, n принята следующая классификация типов образующихся стоячих волн:

· осевые, когда два из трех коэффициентов равны нулю,

· касательные, когда один из коэффициентов равен нулю,

· косые, когда ни один из коэффициентов не равен нулю.

Осевые волны отражаются только от одной пары противоположных параллельных преград (стен), касательные – от двух пар (т.е. устанавливаются в плоскости, параллельной третьей паре преград), косые – от всех пар преград. Для многих материалов коэффициенты поглощения зависят от угла падения волны на преграду. В связи с этим волны разных типов затухают с разной скоростью. Затухание получается наибольшим для косых волн и наименьшим для осевых. Поэтому, когда источник звука возбуждает колебания разных типов, то различные собственные колебания, даже с близкими частотами, будут затухать с неодинаковой скоростью. В результате кривая спада интенсивности звука не будет иметь регулярного вида, который предписывается статистической теорией. Крутизна спада уровня на разных стадиях отзвука будет различной, и тогда теряется определенный смысл самого понятия времени реверберации. Процесс спада будет складываться из разных частных процессов и значит не будет изображаться экспоненциальной кривой, а будет следовать ей лишь в среднем. На него будут накладываться небольшие флуктуации штриховой линией. Практика показывает, что наличие малых флуктуаций благоприятно сказывается на оценке качества звучания. Поэтому значение статистической теории не только не снижается, а, наоборот, приобретает новую опору в выводах волновой теории. Итак, в статистической теории ход спада интенсивности рассчитывается методами теории вероятности, “в среднем”, а флуктуации фактического спада относительно усредненной формы определяются методами волновой теории.шИз волновой теории вытекает, что помещения простой правильной геометрической формы менее удовлетворяют условию диффузности поля, чем помещения сложной геометрической формы с непараллельными стенами, косо поставленными плоскостями или выпуклыми поверхностями, углублениями в виде кессонов. Разумеется, линейные размеры этих поверхностей должны быть соизмеримы с длиной волны или быть больше ее.

Касательные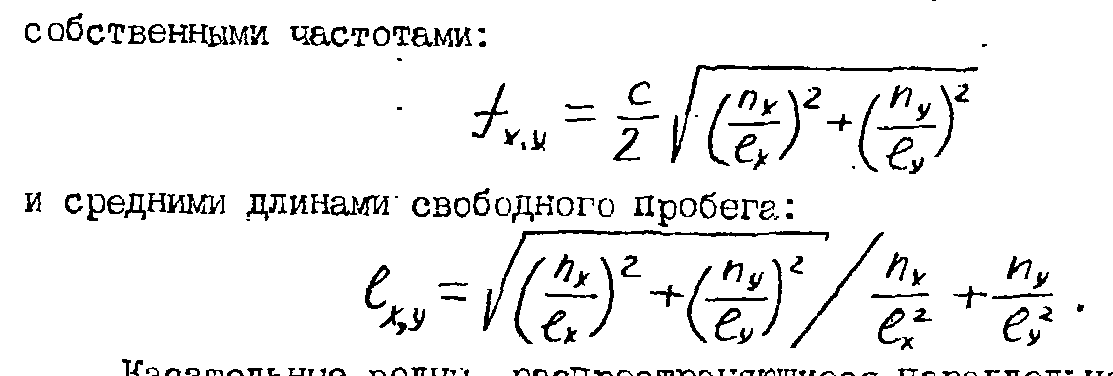

Косые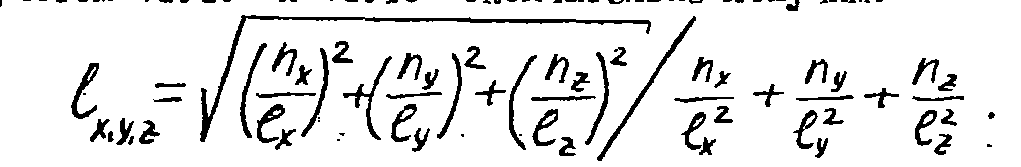

Осевые 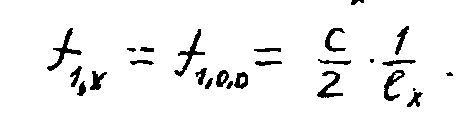для первой частоты

l=l_x