Логарифмические уровни (уровень интенсивности, уровень звукового давления), способы их вычисления в звуковых полях одиночных и групповых излучателей

Простая колебательная система. Механическое сопротивление и его компоненты. Частотные характеристики.

С 429

Простая колебательная система является составной частью почти любого ЭАА. Она состоит из жесткого поршня 1, прикрепленного к опоре подвесом 3 в виде гофрированного воротника, зажатого по внешнему периметру опорными кольцами 5, или с помощью спиральной пружины 2, второй конец которой заделан в опору 4.

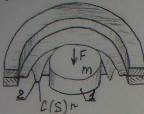
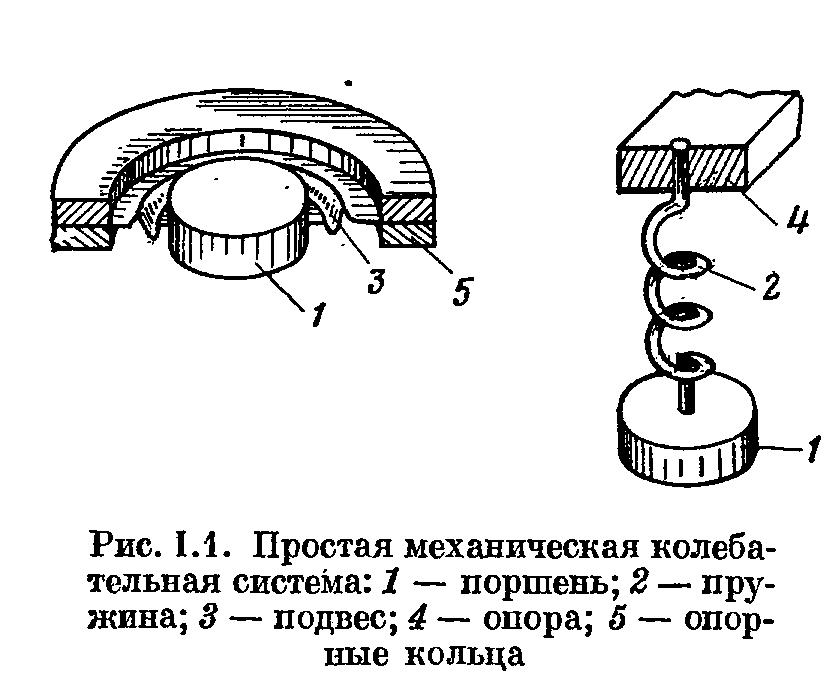
Жесткий диск массой m

с – коэффициент гибкости пружины

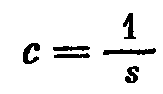(s-коэффициент упругости пружины, численно равный силе, под действием которой получается единичное смещение ее конца)

F=s*ξ – смещение конца пружины

Закон Гука: s=F/ ξ

Сила в каждый момент времени встречает противодействие, обусловленное инерцией поршня, упругостью пружины подвеса и трением.

Реакция, вызываемая инерцией, пропорциональна массе поршня m и приобретенному им к моменту времени t ускорению:

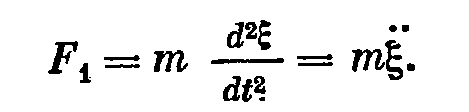
Смещения, с которыми приходится иметь дело в акустике, весьма незначительны по величине, поэтому деформация пружины подвеса, как правило, не переходит за пределы закона Гука и ее реакцию можно считать пропорциональной относительному смещению концов:

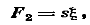или

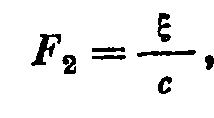
Коэффициент гибкости численно равен смещению ее конца под воздействием единичной силы.

Трение может быть: сухим (кулоновским), вязким (жидкостным- трение о воздух(воду)), внутренним(внутреннее трение пружины).

F₃ =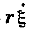

Силы 1,2,3 – внутренние силы массы, гибкости и трения (силы противодействия этих элементов внешней силе)

На основе принципа Даламбера можем составить теперь уравнение равновесия системы:

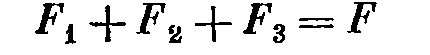Или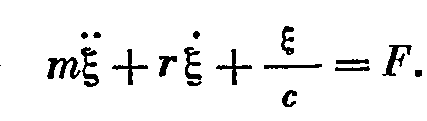

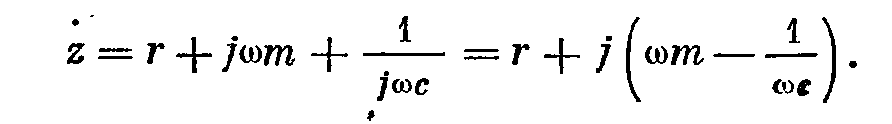- отношение силы к скорости называется полным механическим сопротивление колебательной системы и состоит из трех парциальных сопротивлений – активного r, инерционного jwm и упругого 1/jwc. Два последних – реактивное сопротивление.

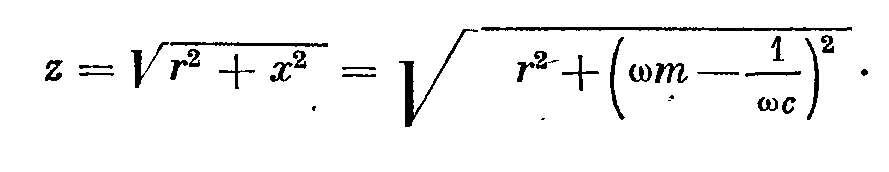- модуль, используется при расчете.

При 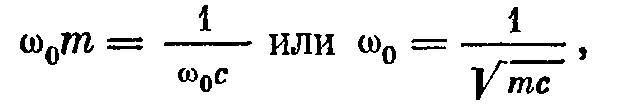реактивная часть полного механического сопротивления исчезает, модуль принимает минимальное значение, равное активному сопротивлению. А колебательная скорость будет максимальной – резонанс, а w₀ – резонансная частота.

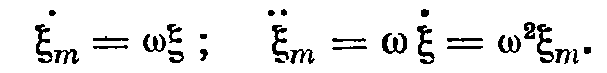
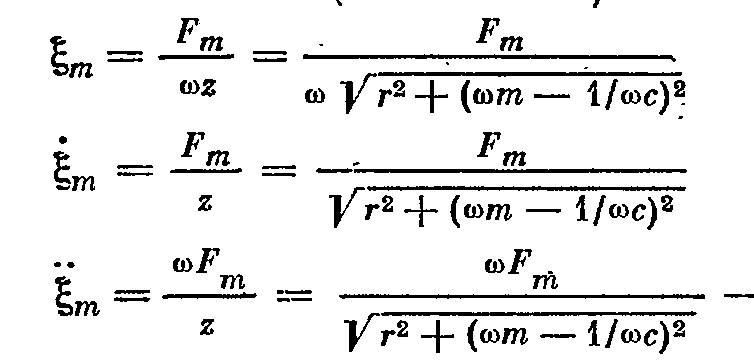
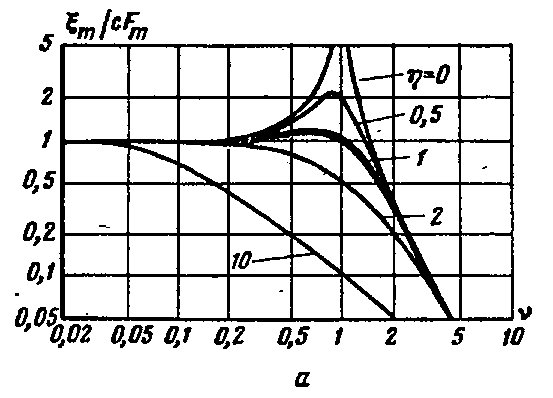
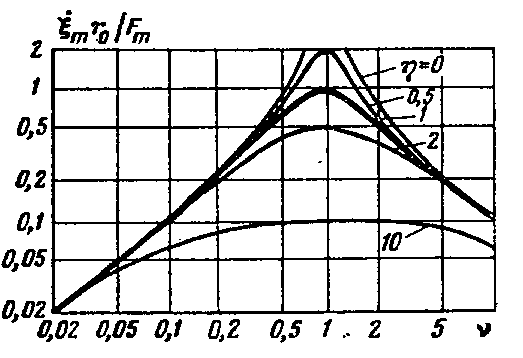
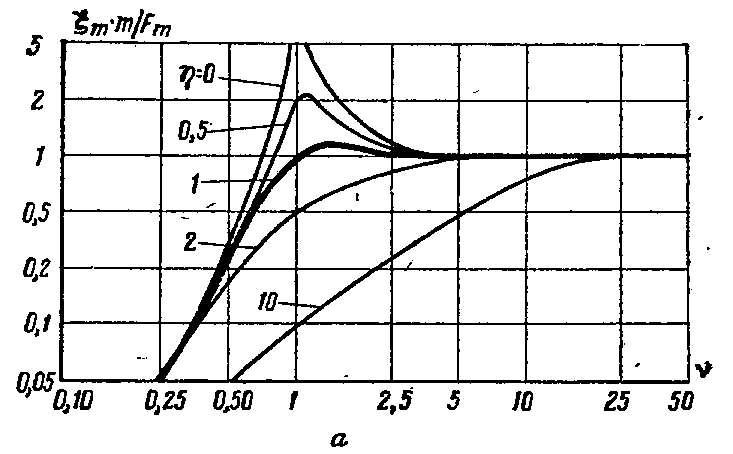
Зная это, построим частотные зависимости амплитуд смещения, скорости и ускорения.

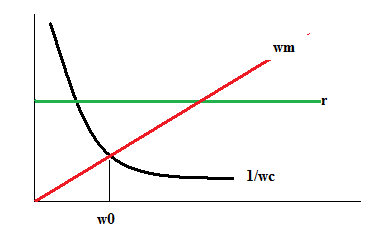
Реактивные составляющие работают друг против друга

До резонанса – преобладает упругое сопротивление,

После – инерционное

На резонансе – активное

На резонансной частоте реактивные сопротивления равны, при этом каждое из них равно характеристическому сопротивлению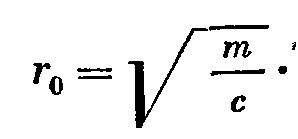

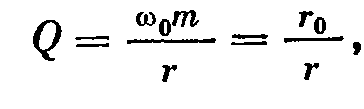-добротность

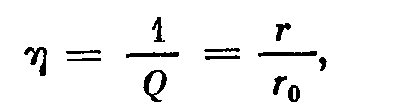-коэффициент потерь

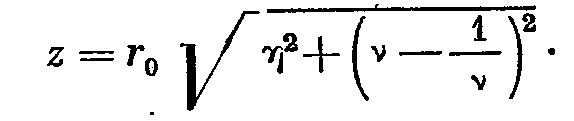
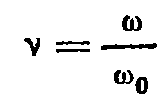
1. Методика анализа сложных механических колебательных систем с помощью динамических моделей и эквивалентных схем.

С 436

Анализ сложных механических систем осуществляется методом электромеханических аналогий.

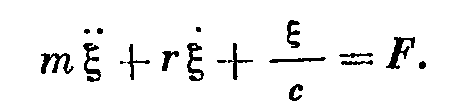
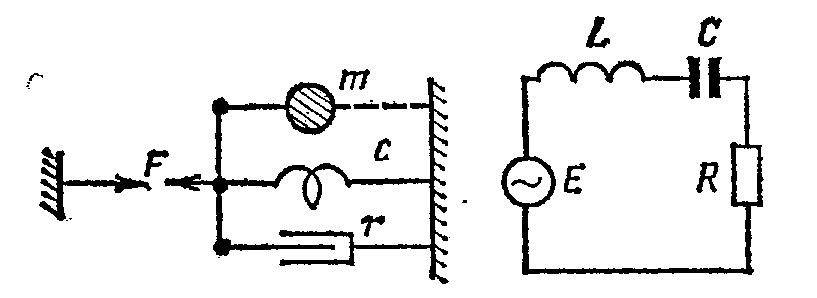
Электрические колебания в контуре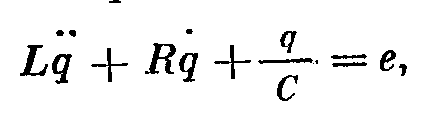

L-индуктивность контура

R – активное сопротивление

С – емкость

e – мгновенное значение приложенной к контуру ЭДС

q- мгновенное значение заряда(с точкой – тока)

В основу аналогии положено соответствие между колебательной скоростью и током. В механической системе сила вызывает колебания со скоростью, в электрической – ЭДС(или напряжение) вызывает ток. для простейших систем составление эквивалентных схем – несложно. Для сложных механических систем рассмотрим один из методов составления эквивалентных схем, предложенный Беловым:

1.замена каждого подвижного узла(жесткое соединение полюсов нескольких элементов, движущихся совместно) механической модели последовательным электрическим контуром, составленным из аналогов тех элементов, полюса которых образуют один узел

2.совмещение одинаковых элементов, входящих в разные контуры.

Анализ механико-акустической системы:

1.идентификация элементов, структуры, масс

-сначала массы, второй полюс всегда на опоре

-затем пружины

-все трения

2.составление динамической модели, которое начинается с обозначения опор и цепочечного размещения между ними всех масс, затем пружины, сопротивления. Соединения отражает узловые структуры

3.сопостовление размещения полюсов элементов в конструкции

3.звуковое поле. Параметры звукового поля. Свойства звуковых полей, создаваемых источниками различных волн: сферических, плоских, промежуточными формами фронта. Характеристика направленности источника звука.

С 6-7,21,24

Звуковой волной называется процесс распространения деформаций сжатия или разрежения в сплошной среде, происходящий с конечной скоростью, называемой скоростью звука.

Звуковая волна может возникать и распространяться только в такой среде, которая обладает определенной упругостью (сжимаемостью) и инерционностью (плотностью).

Область среды, в которой возбуждены звуковые волны – звуковое поле.

Звуковая волна является продольной волной, то есть частицы среды при распространении такой волны совершают колебания вдоль направления распространения.

Фронтом волны называют поверхность, проходящую через частицы среды, совершающие в результате распространения волны колебания с одной и той же фазой. Обычно рассматривают три типа звуковых волн: плоские – фронт в виде плоскости (поршень в трубе); шаровые (ГГ) – с фронтом в виде сферы и цилиндрические – фронт в виде боковой поверхности цилиндра(проезжающий поезд)

Математически звуковая волна описывается волновым уравнением:

В декартовых координатах

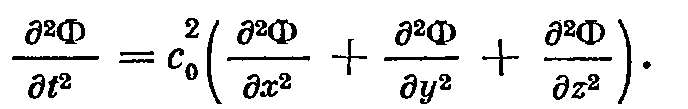
Свойства плоской волны:

1.звуковое давление и колебательная скорость совпадают по фазе, это говорит о чисто активном характере звуковой энергии, переносимой плоской волной.

2.звуковое давление и колебательная скорость не зависят от расстояния(для идеальной среды)

3.волновое сопротивление плоской волны -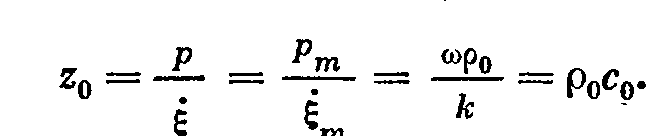

Свойства шаровой волны:

Фронт волны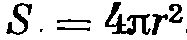

1.амплитуда звукового давления в шаровой волне изменяется обратно пропорционально расстоянию

2. колебательная скорость в поле шаровой волны имеет 2 составляющие – одна из них совпадает по фазе с давлением и называется активной, вторая отстает на 90 градусов – реактивная.

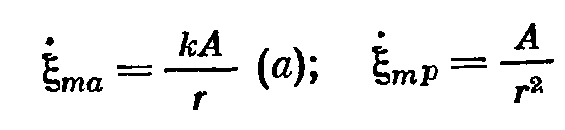
Характеристика направленности источника звука – диаграмма в полярных координатах, показывающая распределение звукового давления в зависимости от угла склонения θ (угол между осью излучения и направлением на данный приемник).

R(θ) = P(θ)/P(0°)

R(θ) = 0.5(1+cos θ) «кардиоида»

R(θ) = cos θ «восьмерка»

Разновидности характеристик направленности:

1.слабонаправленные

2.ненаправленные

3.остронаправленные (угол направленного действия меньше 45).

Акустическая мощность источника звука, интенсивность звука (определение понятий). Взаимосвязь акустической мощности источника с осевой интенсивностью на заданном расстоянии. Понятие коэффициента осевой концентрации.

ТОА пункт 3.4.2

Акустич. мощность = колебательная скорость в квадрате умножить на сопротивление излучения

Формулы и графики оттуда

Анализ показывает, что в НЧ излучаемая мощность круто спадает с уменьшением частоты ( 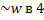), в третьей зоне – ОВЧ: сопротивление излучения перестает расти, но система продолжает управляться массой. Колебательная скорость уменьшается, отсюда следует, что мощность падает обратно пропорционально частоте в квадрате. В средней части – оптимизация характеристики, она становится равномерной по той причине, что уменьшение колебательной скорости (ее квадрата) компенсируется квадратичным возрастанием сопротивления излучения.

Интенсивность звука – средний поток звуковой энергии, проносимой звуковой волной в одну секунду через единичную площадку, нормальную к направлению распространения звука. Измеряется в Вт/м².

Для шаровой волны -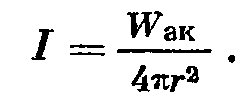

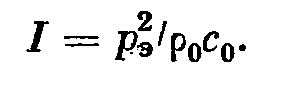- для любого фронта.

Для ненаправленного I= W_АК/4Пr²

Для направленного I= (W_АК/4Пr² )*Ω

КОК – отношение акустических мощностей ненаправленного и направленного источников, создающих на одном и том же расстоянии на оси одинаковую интенсивность.

Или КОК – отношение квадрата осевой чувствительности в условиях свободного поля к его значению, усредненному по всем направлениям на одной и той же частоте.

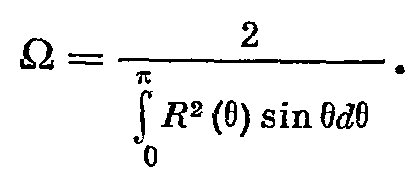
логарифмические уровни (уровень интенсивности, уровень звукового давления), способы их вычисления в звуковых полях одиночных и групповых излучателей

С41

Ощущения сенсорных органов пропорционально не линейной величине раздражения, а его логарифму.

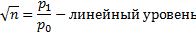
N=lgn, так как 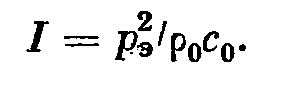, то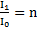

Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J₀ равен

Уровень интенсивности звука = 10 lg (J/J₀) дБ

Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.

В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Р₁. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р₀, получают так называемый уровень звукового давления.

Уровень звукового давления = 20 lg (P₁/P₀) дБ

Условное давление Р₀ = 2*10^—5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц.

Складывать дБ нельзя, надо переводить в интенсивности!

Децибе́л — логарифмическая единица уровней, затуханий и усилений.