Колебания в гликолизе

Колебательные процессы в биологии. Автоколебательные режимы. Предельные циклы и их устойчивость. Примеры.

Колебательные прцессы наблюдаются во многих биологических процессах (гликолиз, фотосинтез, колебания численности видов и т.д)

Автоколебательными называются системы, в которых устанавливаются и поддерживаются незатухающие колебания за счёт сил, зависящих от состояния самой системы. Амплитуда этих колебаний определяется свойствами самой системы и не зависит от внешних условий. На фазовой плоскости, решение системы, описывающей автоколебательные системы, представляется предельным циклом. Обязательное условие существования предельного цикла – открытая система

Рисунок 1

Отличие предельного цикла от траекторий вокруг особой точки типа «центр» в том, что после небольших возмущений система вновь возвращается на исходную траекторию.

Колебания в гликолизе

В упрощённой модели гликолиза после разделения переменных на быстрые и медленные остались стадии превращения глюкозы в Ф6Ф (фруктозо-6-фосфат) и его переход в ФДФ фруктозодифосфат) под действием ФФК (фосфофруктокиназы)

Гл→ ^υ1 Ф6Ф→^υ2ФДФ→^υ3

Проявление автоколебательных свойств наблюдается, когда в модели присутствуют нелинейные члены. Этому требованию соответствовало предположение, что ФФК активируется продуктом превращения – фруктозодифосфатом.

Обозначим концентрацию Ф6Ф за х,а ФДФ – за y

υ1 (скорость поступления Ф6Ф) считается постоянной, зависящей от избыточной концентрации глюкозы. υ2 (превращение Ф6Ф в ФДФ) = kx = k’xy (автокатализ). υ3 (отток ФДФ) = k2y. Но! данные уравнения не учитывают насыщение скорости при ферментативном катализе: υ = kx/(Kx +x)

Получаем систему уравнений:

dx/dt = υ1 – υ2 = υ1 – (k1*x*y)/[(Kx+x)*(Ky+y)]

dy/dt = υ2 – υ3 = (k1*x*y)/[(Kx+x)*(Ky+y)] – k2*y/(K’y+y)

Предполагаем, что Ky>>y, Kx>>x и вводим безразмерные переменные: x’ = x/x(стационар.), y’=y/y(стационар.)

При анализе выяснилось, что характер фазового портрета меняется в зависимости от соотношения параметров a и r. a ~ 1/ (υ1*k1), r = y(стационар.)/K’y

Параметр а можно рассматривать, как управляющий (его значение можно менять, варьируя концентрацию глюкозы во внешней среде)

При a*r/(1+r)<1 особая точка является устойчивым фокусом. При a*r/(1+r)>1 особая точка является неустойчивым фокусом. Во втором случае возможно образование предельного цикла. Значение a*r/(1+r)=1 – бифуркационное.

Видно, что колебания присутствуют в голодных клетках. Эксперименты показали, что активация ФФК происходит, но не ФБФ, а АДФ и АМФ, и ингибируется АТФ

Колебания при субстратном и продуктном неконкурентном угнетении:

S+ES↔ESS

P+ES↔ESP

P+E↔EP

P+ESS↔ESSP

Схема реакции – рисунок 2

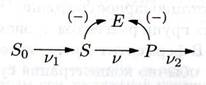
dS/dt = υ1 – υ(S,P)

dP/dt = υ(S,P) – υ2

Число и устойчивость стационарных состояний данной системы зависят от глубины продуктного угнетения При слабом угнетении концентрация субстрата будет быстрой переменной по сравнению с концентрацией продукта. При этом реализуется единственное неустойчивое стационарное состояние на неустойчивой части характеристики υ(S) (отрезок АВ) Автоколебания возникают на фазовой плоскости S, P при движении вдоль цикла С→A→D→B→C

Рисунок 3

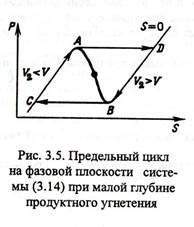
Движение по устойчивой ветке СА совершается с накопление продукта. В критической точке А при υ2 = υ система скачком переходит в точку D ветви DB, где концентрация продукта начинает убывать, а скорость υ растёт. В точке В при υ2 = υ система вновь срывается и уходит в точку С

Общие условия возникновения автоколебательных режимов в полиферментной последовательности реакций

1. Один из реагентов должен ускорять собственное образование.

2. Другой реагент должен подавлять собственное образование

3. Должны существовать перекрёстные взаимодействия реагентов противоположного характера (повышение концентрации одного должно вызывать уменьшение концентрации другого)