Обработка результатов прямых многократных измерений

Смысл задачи обработки многократных (статистических) измерений состоит в том, чтобы получить оценку действительного значения измеряемой величины и определить погрешность этой оценки.

Способ обработки результатов статистических измерений зависит от вида распределения. Наиболее хорошо отработаны методы обработки экспериментальных данных, если их распределение не противоречитнормальному закону. Но для того, чтобы этими методами можно было воспользоваться, необходимо прежде доказать, что распределение опытных данных не противоречит нормальному закону. Главным фактором, затрудняющим идентификацию закона распределения, является всегда относительно малое количество экспериментальных данных. В этом случае следует максимально использовать априорную информацию о виде распределения погрешностей. Эта информация заключается в том, что кривая плотности распределения предполагается плавной и симметричной.Плавной кривая должна быть потому, что (в подавляющем большинстве случаев) сама измеряемая величина является непрерывной. Предположение о симметрии базируется на относительной малости размера погрешности. Его также можно считать справедливым, так как в большинстве случаев, представляющих практический интерес, величина относительной погрешности измерений находится в интервале значений от долей, до нескольких единиц процента. Для того, чтобы использовать вероятностно-статистические методы при обработке результатов многократных измерений, систематические погрешности должны быть исключены (т.е. все результаты исправлены), либо должно быть заранее известно, что случайные погрешности много больше систематических. Промахи из совокупности опытных данных должны быть исключены экспериментатором.

Задача обработки прямых многократных измерений может формулироваться в двух вариантах:

1. Обработка результатов многократных измерений, когда заранее известно, что закон распределения опытных данных нормальный. Количество опытных данных в этом случае может быть 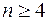.Обработка результатов в этом случае ведется по формулам (1.16-1.22;1.30) и результат представляется в виде (1.31).

2. Обработка результатов многократных измерений, когда закон распределения заранее неизвестен. В этом случае вначале необходимо идентифицировать закон распределения опытных данных, чтобы затем применить соответствующие вероятностно-статистические методы обработки данных. Для уверенной идентификации закона распределения количество опытных данных n должно быть 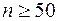(хотя эта граница достаточно условна).

Для того, чтобы достаточно обоснованно выдвинуть гипотезу о виде закона распределения, экспериментальные данные группируют и выборку представляют в виде гистограммы, состоящей из r столбцов с определенной протяженностью (h) соответствующих им интервалов. По виду полученной гистограммы и формулируется гипотеза о законе распределения опытных данных, которую затем подтверждают с использованием соответствующего критерия согласия (либо отвергают и выдвигают новую, которую также предстоит затем подтвердить). При построении гистограммы следует соблюдать некоторые общие правила. [8]

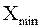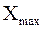Опытные данные упорядочивают (представляют в виде вариационного ряда от до в порядке возрастания), и группируют по интервалам. Ширину интервалов обычно выбирают одинаковой, равной h

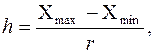(1.47)

где r - количество интервалов разбиения.

Число интервалов разбиения нельзя выбирать очень большим или очень малым. При группировании данных в большое число мелких интервалов некоторые из них окажутся пустыми. Гистограмма будет иметь “гребенчатый” вид, то есть резко отличаться от плавной кривой. Следовательно, если внутри гистограммы получаются пустые интервалы, это, чаще всего, говорит о том, что число интервалов разбиения выбрано слишком большим.

При очень малом числе интервалов будут потеряны характерные особенности опытного распределения. Так, например, при трех интервалах любое колоколообразное распределение сведется к треугольному. Задача оптимального выбора количества интервалов не имеет в общем виде строгого решения. Для практических целей можно выбирать число интервалов r, руководствуясь таблицей 1.3, приводимой ниже [5].

Таблица 1.3

Предпочтительно выбирать r нечетным, чтобы принудительно не уплощать островершинные распределения.

Значение ширины интервала h определенное из (1.47) нужно всегда округлять в большую сторону (например, 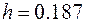округляют до 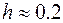), причем желательно, чтобы h легко делилось на 2 (для определения координат центров столбцов).

Нижняя граница первого интервала не обязательно должна быть равной 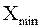. Эта граница может быть выбрана несколько меньше 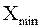но так, чтобы границы всех интервалов получались удобными для построения гистограммы (например, пр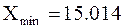и и 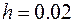, целесообразно выбрать 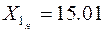, тогда 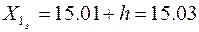и т.д.)

Масштаб по осям при построении гистограммы рекомендуется выбирать так, чтобы высота графика относилась к его основанию как 3 к 5 . При этом общая площадь между осью абсцисс и ступенчатой кривой должна быть равной единице (условие нормировки).

Если из построенной гистограммы следует, что кривая опытного распределения имеет форму близкую к колоколообразной, целесообразно первой проверить гипотезу о нормальности распределения опытных данных.

22. Электронно-счетный частотомер: принцип действия, структурная схема, основные соотношения, погрешность дискретности.

Цифровой (дискретного счета) метод измерения частоты реализован в цифровых электронно-счетных частотомерах. Данные приборы удобны в эксплуатации , имеют широкий диапазон измеряемых частот (от нескольких герц до сотен мегагерц) и позволяют получить результат измерения с высокой точностью (относительная погре-шность измерения частоты 10^–6…10^–9).

Цифровые частотомеры являются многофункциональными приборами, в зави-симости от режима их работы можно проводить измерение не только частоты, но и интервалов времени (периода следования периодических сигналов)

Принцип измерения частоты гармонического сигнала цифровым методом поясняет рис.8, где приведены структурная схема цифрового частотомера в режиме измерения частоты и временные диаграммы к его работе.

Исследуемый гармонический сигнал, имеющий частоту f_X , подается на входное устройство (ВУ), усиливающее или ослабляющее его до значения, требуемого для рабо-ты последующего устройства частотомера (рис.,8,а)

Снимаемый с выхода ВУ гармонический сигнал u₁ (рис.8,б) поступает на первый формирователь импульсов (Ф1), преобразующий его в последовательность коротких однополярных импульсов u₂, следующих с периодом T_X = 1/f_X и называемых счетными.

Причем передние фронты этих импульсов практически совпадают с моментами перехода сигнала u₁ через нулевое значение на оси времени при его возрастании. Формирователь Ф1 состоит из усилителя-ограничителя и компаратора (триггера Шмитта).

Счетные импульсы u₂ поступают на один из входов временнóго селектора (ВС), на второй вход которого от устройства формирования и управления (УФУ) подаётся строб---импульс u₃ прямоугольной формы и калиброванной длительности T_O>T_X. Интервал времени T_O называется временем счета (“временными воротами”). Временной селектор открывается строб-импульсом u₃ и в течение егодлительности пропускает группу (пакет) импульсов u₂ на вход счетчика (СЧ). В результате на счетчик поступает пакет из N_X импульсов u₄.Из рис.8,б следует, что

T_O = N_X·T_X – Δt_H + Δt_K = N_X·T_X – Δt_д, (2.4)

где Δt_H и Δt_K – погрешности дискретизации начала и конца интервала T_O ,вызванные случайным положением строб-импульса отностиельно счктных импульсов u₂; Δt_д = Δt_H – Δt_K – общая погрешность дискретизации.

Пренебрегая в (2.4) погрешностью Δt_д ,получаем , что число импульсов в пакете N_X = T_o/T_X = T_o·f_X и, следовательно, измеряемая частота пропорциональна числу счетных импульсов, поступающих на счетчик:

f_X =N_X/T_o. (2.5)

Для формирования строб-импульса на устройство УФУ поступают короткие импульсы с периодом T_o (на рисунке для упрощения не показаны) от схемы, включающей генератор образцовой частоты (ГОЧ) и второй формирователь импульсов (Ф2), аналогичный формирователю Ф1. В составе ГОЧ имеется кварцевый генератор образцовой частоты f_КВ и декадный делитель частоты с коэффициентом деления К_Д (каждая декада уменьшает частоту f_КВ в десять раз). Период импульсов на выходе формирователя Ф2 и длительность строб-импульсов равны периоду сигнала на выходе делителя частоты , т.е. T_o = К_Д/f_КВ; поэтому выражение (2.5) можно представить в виде

f_X = N_X·f_КВ/К_Д (2.6)

Отношение f_КВ/K_Д можно дискретно изменять вариацией К_Д,т.е. за счет изменения числа декад делителя Д (генератора ГОЧ).

Счетчик подсчитывает N_X импульсов и выдает соответствующий (двоичный) код в цифровое отсчетное устройство (ЦОУ). Отношение f_КВ/K_Д выбирается равным 10ⁿ Гц, где n – целое число. При этом ЦОУ отображает число N_X , соответствующее измеряемой частоте f_X в выбранных единицах. Например, если за счет изменения К_Д выбрано n = 6, число то число N_X , отображаемое на ЦОУ, соответствует частоте f_X ,выраженной в МГц.

Циклический режим работы частотомера задаётся УФУ, при этом перед началом каждого измерения УФУ сбрасывает показания счетчика в ноль.

Погрешность измерения частоты f_X имеет систематическую и случайную составляющие

Систематическая составляющая вызывается в основном температурной неста-бильностью частоты кварцевого генератора f_КВ. Её уменьшают путем термостатирования кварца или за счет применения в кварцевом генераторе элементов с термокомпкнсацией.

Случайная составляющая определяется погрешностью дискретизации Δt_Д = Δt_H – Δt_K.

Поскольку взаимная синхронизация строб-импульса (“временных ворот”-T_o) и счетных импульсов отсутствует, погрешности Δt_H и Δt_K ,определяющие на рис.8,б положение начала и конца строб импульса между соседними двумя счетными импульсами, могут принимать во времени с одинаковой вероятностью значения от нуля до T_o. Поэтому погрешности Δt_H и Δt_K являются случайными и распределены по равномерному закону.

23. Цифровой фазометр с усреднением: принцип действия, структурная схема, основные соотношения, источник погрешности.

Формирователь Ф формирует импульсы длительностью ΔТ, пропорциональной измеряемому фазовому сдвигу. Ключ КЛ1 открывается на время ΔТ и пропускает N счетных импульсов частотой fо с генератора образцовой частоты ГОЧ. Ключ КЛ2 открыт на длительное время измерения Тизм , формируемое устройством управления УУ с помощью делителя частоты ДЧ из импульсов высокостабильного ГОЧ. При этом время Тизм для постоянной частоты входного сигнала обычно выбирается кратным периоду входных сигналов, т. е. Тизм = m-Т . Тогда счетчик за время Тизм подсчитает число импульсов:

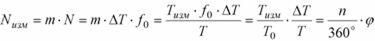
n- коэффициент деления делителя частоты.

Недостаток: большое время измерения , зависящее от частоты исследуемого сигнала и необходимой точности измерений.

Погрешность:

-нестабильность ГОЧ

-дискретность кодирования интервала

24. Светолучевые осциллографы: принцип действия, функциональная схема, области применения.

В диапазоне до 20 КГц применяют светолучевые осциллографы, в которых запись осуществляется с помощью специальных гальванометров лучом света на фотобумаге или фотопленке, а также ультрафиолетовым лучом на специальной бумаге, самопроявляющейся на свету. Хорошая точность, чувствительность, многоканальность (до 10 и более), малые габаритные размеры являются причиной широкого применения этих приборов. Для регистрации более высокочастотных процессов используют электронно-лучевые осциллографы с фотографированием процесса с экрана ЭЛТ.

Шлейфовый осциллограф, светолучевой, вибраторный осциллограф, прибор для визуального наблюдения и автоматической регистрации фотографическим методом физических процессов (например, деформации, изменений температуры, давления, скорости), периодических (с частотой повторения от долей гц до 10-15 кгц), апериодических и одиночных. На входе Ш. о. изменение физической величины, характеризующей исследуемый процесс, преобразуется соответствующими датчиками в пропорциональное изменение электрического напряжения или тока.

Рис2 Шлейфовый осциллограф (схема устройства)

Ш. о. состоит (см. рис 2.) из одного или нескольких магнитоэлектрических зеркальных гальванометров (шлейфов) светооптической системы, блока протяжки (на рис. не показан), носителя записи (светочувствительной бумаги или фотоплёнки) и устройства визуального наблюдения. Светооптическая система формирует световой луч, фокусирует его и направляет на зеркало шлейфа. Отразившись от зеркала, луч попадает на светочувствительную плёнку (бумагу) и оставляет на ней след в виде кривой, отображающей изменение исследуемой физической величины во времени. Развёртка кривой во времени обеспечивается равномерным перемещением носителя записи в направлении, перпендикулярном отклонению светового луча. Скорость движения носителя записи у различных Ш. о. регулируется в пределах от 1 до 10 000 мм/сек. Для визуального наблюдения записываемой кривой служит сферический матовый экран, на который попадает часть светового луча, отражённого зеркалом шлейфа. Развёртка во времени визуально наблюдаемой кривой осуществляется с помощью равномерно вращающегося многогранного зеркального барабана. При вращении барабана луч света, отражаясь от его зеркальных граней, периодически пробегает по экрану. Регулируя частоту вращения барабана, можно добиться неподвижного изображения кривой.

Для одновременной регистрации нескольких физических величин используют т. н. многоканальные Ш. о., содержащие от 4 до 60 шлейфов, обеспечивающих одновременную запись соответствующего числа кривых. Ш. о. широко применяются при научных исследованиях, лабораторных и производств. испытаниях

25. Магнитоэлектрические измерительные приборы: основные параметры, примеры конструкций, уравнение шкалы, области применения.

Устройство магнитоэлектрического ИМ показано на рис. 1.1. Работа его основана на взаимодействии подвижной рамки 5, обтекаемой током, с полем постоянного магнита 1. Это поле с помощью магнитопровода 2, полюсных наконечников 3 и цилиндрического сердечника 4, изготовленных из магнитомягкого материала, концентрируется в зазоре, где движется рамка 5, соединенная полуосью 8 со стрелкой 6. Рамка 5 намотана на легком алюминиевом каркасе, в котором при движении возникают вихревые токи, способствующие успокоению ее колебаний. Ток подводится к рамке через спиральные пружинки 7, создающие противодействующий момент.

При протекании по обмотке рамки постоянного тока 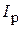на нее действует вращающий момент

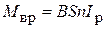, (1.1)

где 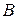– индукция магнитного поля в зазоре; 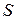– площадь рамки; n – число витков обмотки рамки.

Учитывая, что противодействующий момент пропорционален углу поворота рамки, из выражения (1.1) можно найти угол отклонения, при котором наступает равновесие подвижной части ИМ

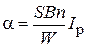. (1.2)

где 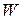– коэффициент, зависящий от упругости пружинки. Коэффициент пропорциональности между углом отклонения и силой тока называется чувствительностью ИМ по току. Как следует из (1.2), при постоянстве индукции в зазоре чувствительность магнитоэлектрического ИМ постоянна и шкала линейна.

При протекании по обмотке рамки меняющегося во времени тока i(t) выражение (1.1) будет описывать связь мгновенных значений тока рамки и действующего на нее вращающего момента.

Если частота изменения тока намного меньше частоты собственных механических колебаний подвижной части ИМ, то отклонение рамки определяется мгновенными значениями ее тока. Такой режим работы характерен для регистрирующих приборов, например, самописца.

Частота собственных механических колебаний рамки мала и в большинстве случаев при проведении радиоизмерений частота тока рамки значительно превосходит ее. В этом случае угол отклонения рамки пропорционален постоянной составляющей ее тока

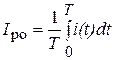, (1.3)

где 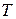– постоянная времени подвижной части ИМ.

Приборы магнитоэлектрической системы применяются в гальванометрах, вольтметрах и амперметрах постоянного тока. Показания этих приборов не зависят от влияния внешних магнитных полей. Они мало расходуют энергии при работе, имеют быстрое успокоение, большую точность, высокую чувствительность, равномерную шкалу измерений.