Погрешности прямых измерений с многократными наблюдениями
Пусть хi – результат i-го измерения (i = 1,2, ..., n).
Среднее арифметическое значение ряда измерений (оценкаматематического ожидания mx, соответствующего для физической величины ее истинному значению):
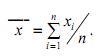
Отклонение результата каждого измерения от среднего значения (остаточная погрешность):
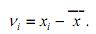
Значение среднеквадратической погрешности ряда измерений
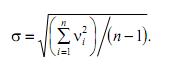
Среднеквадратическое отклонение среднего арифметического значения
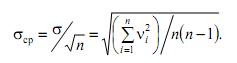
Значением σ пользуются в том случае, если необходимо дать характеристику точности применяемого метода измерения: если метод точен, то разброс результатов отдельных измерений мал, т.е. мало значение σ. Значение σср используется для характеристики точности результата измерений некоторой величины, т.е. результата, полученного посредством математической обработки итогов целого ряда отдельных прямых измерений. При оценке погрешностей измерений пользуются понятиями доверительная вероятность» и соответствующий ей «доверительный интервал».
Введем важные понятия доверительной вероятности и доверительного интервала. Как указывалось выше, среднее арифметическое значение , полученное в результате некоторого ряда измерений, является оценкой истинного значения Хи и, конечно, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Pд есть вероятность того, что отличается от Хи не более чем на Δ, т.е. 
Либо 
Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от - Δ до + Δ - доверительным интервалом.
Приведенные выше неравенства означают, что с вероятностью Рд доверительный интервал от - Δ до + Δ заключает в себе истинное значение Хи. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами - доверительной вероятностью и соответствуюшим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (и < 20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших n, но значительно отличающуюся от нормальной при малых n.
Все это справедливо для достаточно большого числа измерений, когда 
(СКО среднеарифметического) близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента.Это распределение вероятностей случайной величины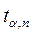 
, называемой коэффициентом Стьюдента, дает значение доверительного интервала 
в долях средней квадратичной ошибки среднего арифметического .
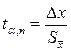. (4)
Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса. Функция распределения табулирована (Т.е. значения искать в таблице надо). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α.
При обработке результатов прямых измерений рекомендуется принять следующий порядок выполнение операций.
- Проводятся измерения заданного физического параметра n раз в одинаковых условиях, и результаты записываются в таблицу.
- Если результаты некоторых измерений резко отличаются по своему значению от остальных измерений, то они как промахи отбрасываются, если после проверки не подтверждаются.
- Вычисляется среднее арифметическое
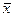из n одинаковых измерений. Оно принимается за наиболее вероятное значение измеряемой величины
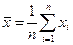. (8)
- Находятся абсолютные погрешности отдельных измерений
- Вычисляются квадраты абсолютных погрешностей отдельных измерений (Δхi)2
- Определяется средняя квадратичная ошибка среднего арифметического
.
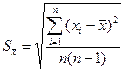- Задается значение доверительной вероятности α. В лабораториях практикума принято задавать α=0,95.
- Находится коэффициент Стьюдента
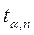для заданной доверительной вероятности α и числа произведенных измерений (см.табл.) - Определяется случайная погрешность
.
- Определяется суммарная погрешность
.
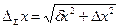где δх – приборная погрешность, Δх – случайная погрешность.
- Оценивается относительная погрешность результата измерений
.
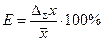- Записывается окончательный результат в виде
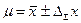, с α=… Е=…%.
14. Виды погрешностей.
1) по форме выраженияпогрешности подразделяют на абсолютные и относительные. Погрешность, выраженная в единицах измеряемой величины, называется абсолютной. Если измеренная величина превышает действительное значение, погрешность положительна, если же действительное значение больше измеренного – отрицательна. Абсолютная погрешность характеризует качество измерений только однородных величин примерно одинакового размера.
Относительной погрешностью называется отношение абсолютной погрешности к истинному значению измеряемой величины: δQ=ΔQ/Qиcт ≈ ΔQ/Qд. Как правило, относительные погрешности выражают в процентах. Относительная погрешность может характеризовать качество измерений, как разнородных величин, так и однородных величин разного размера. Для оценки качества измерения необходимо вычислить относительные погрешности: меньшая погрешность при прочих равных условиях характеризует более высокое качество измерений.
В метрологии пользуются понятием точность измерений, причем точность – величина, обратная относительной погрешности.
2) по причине возникновения погрешности разделяют на две группы: объективные погрешности, не связанные с человеком-оператором, производящим измерения, и субъективные (личные), обусловленные экспериментатором, состоянием его органов чувств, опытом и т.д. В свою очередь, объективные погрешности разделяются на погрешности опознания объекта, методические, инструментальные погрешности и погрешности, обусловленные внешними условиями.
Погрешности опознания объекта измерения связаны с несоответствием реального объекта принятой модели.
Погрешности метода обусловлены несовершенством метода измерений, упрощающими предположениями, принятыми при обосновании метода. К этим погрешностям относятся составляющие погрешности, вызываемые влиянием средства измерения на измеряемую цепь.
Инструментальные погрешности возникают из-за несовершенства средств измерения, их схем, конструкций, состояния в процессе эксплуатации. Каждое средство измерения характеризуется свойственной ему погрешностью, которая входит в общую погрешность измерения.
3) по закономерностям проявления погрешностей различают систематические, случайные, грубые погрешности измерений и промахи.
Систематическая погрешность Δc – это составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в одних и тех же условиях. Закономерно изменяющаяся систематическая погрешность, в свою очередь, может быть прогрессирующей (возрастающей, убывающей), периодической или изменяющейся по сложному непериодическому закону. К постоянным систематическим погрешностям относят, например, погрешность градуировки шкалы, погрешность значения меры, температурную погрешность. К переменным систематическим погрешностям относят погрешности, обусловленные изменением напряжения питания (разряд аккумуляторной батареи), погрешности, связанные с действием электромагнитных помех и т.д.
Систематические погрешности могут быть обнаружены и оценены. Если систематическая погрешность достаточно точно определена, она может быть исключена введением поправки или поправочного множителя.
Поправка – значение величины, одноименной с измеряемой, прибавляемое к измеренной величине для исключения систематической погрешности. Поправка равна абсолютной систематической погрешности, взятой с обратным знаком.
Поправочный множитель – число, на которое умножают результат измерения с целью исключения систематической погрешности.
Случайная погрешность Δсл – составляющая погрешности измерения, которая при повторных измерениях в одних и тех же условиях изменяется случайным образом, т.е. без видимой закономерности. Случайные погрешности являются следствием случайных процессов, протекающих в измерительных цепях. Для оценки погрешностей и разработки способов уменьшения их влияния на результат измерения используют аппарат теории вероятностей и математической статистики. По мере того, как будут изучены отдельные процессы из множества, установлены их закономерности, погрешности из случайных перейдут в категорию систематических.
Таким образом, результат измерения всегда содержит как систематическую, так и случайную погрешности: Δ=Δс+Δсл.
Грубой погрешностью называют погрешность, существенно превышающую погрешность, оправданную условиями измерения, свойствами примененных средств измерений, методом измерения, квалификацией экспериментатора. Грубые погрешности могут появляться вследствие резкого изменения влияющей величины на результат измерения. Грубые погрешности обнаруживают статистическими методами и исключают из рассмотрения.
Промахи являются следствием неправильных действий экспериментатора. Это может быть описка при записи результатов, неправильно снятые показания прибора и т.д. Промахи обнаруживают нестатистическими методами, их следует всегда исключать из рассмотрения.
Также погрешности разделяют на: статические и динамические. Статические погрешности имеют место при статических измерениях, т.е. при неизменной во времени измеряемой величине, динамические – при динамических измерениях, т.е. при переменной во времени измеряемой величине. Динамическая погрешность возникает вследствие инерционности свойств средств измерений. Для оценки динамической погрешности необходимо знать передаточную функцию средства измерения, а также характер изменения измеряемой величины.
15. Кодо-импульсный цифровой вольтметр: принципе действия, пример структурной схемы, временные диаграммы.
В кодоимпульсных цифровых вольтметрах (в вольтметрах с поразрядным уравновешиванием) реализуется принцип компенсационного метода измерения напряжения. Упрощенная структурная схема такого вольтметра представлена на рис. 8.12.
Измеряемое напряжение U‘x, полученное с входного устройства, сравнивается ,с компенсирующим напряжением Uк вырабатываемым прецизионным делителем и источником опорного напряжения. Компенсирующее напряжение имеет несколько уровней, квантованных в соответствии с двоично-десятичной системой счисления. Например, двухразрядный цифровой вольтметр, предназначенный для измерения напряжений до 100 В, может включать следующие уровни напряжений: 80,40,20, 10, 8,4,2,1 В.
Сравнение, измеряемого U‘x и компенсирующего Uкнапряжений производится последовательно по командам управляющего устройства. Процесс сравнения напряжений показан на рис. 8.13. Управляющие импульсы Uy через определенные интервалы времени переключают сопротивления прецизионного делителя таким образом, что на выходе делителя последовательно возникают значения напряжения: 80, 40, 20, 10, 8, 4, 2, 1 В; одновременно к соответствующему выходу прецизионного делителя подключается устройство сравнения.
Если Uк > U'x, то с устройства сравнения поступает сигнал Uср на отключение в делителе соответствующего звена, так, чтобы снять сигнал Uк . Если Uк < U'х ,'то сигнал с устройства сравнения не поступает. После окончания процесса сравнения полученный сигнал Uкод положения ключей прецизион-ного делителя и является тем кодом, который считывается цифровым отсчет-ным устройством.
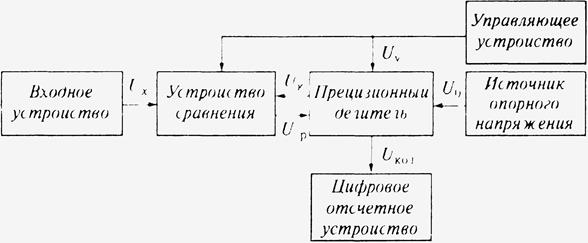
8.12. Упрощенная структурная схема кодоимпульсного вольтметра
На рис. 8.13 для наглядности показан процесс кодирования аналогового напряжения с амплитудой 63 В, из которого видно, что код, соответствующий этому сигналу, будет 01100011.
Процесс измерения напряжения в кодоимпульсном приборе напоминает взвешивание на весах, поэтому приборы иногда зазывают поразрядно-уравновешивающими. Точность кодоимпульсного прибора зависит от стабильности опорного напряжения, точности изготовления делителя, порога срабатывания сравнивающего устройства.
Для создания нормальной помехозащищенности (60…70 дБ) на входе приборов ставится помехоподавляющий фильтр. В целом такой цифровой прибор обладает хорошими техническими характеристиками и используется как лабораторный. Первые цифровые приборы создавались по методу взвешивания, но сейчас более широкое распространение получили приборы вре-мяимпульсного типа.
Uу Импульсы с управляющего устройства
 | | | | | | | | |
0
 | |||
 |
Uк 80В
Поочередное переключение
сигналов с делителя
40В
 |
20В
10В
8В
4В
2В 1В
0
t
Uср Сигналы на выходе устройства
сравнения
1 0 0 1 1 1 0
0
t
ΣUк 1В U׳ x =63В
2В
Суммарное компенсирующее
напряжение Σ 
Uк
20В
 |
40В
 |
0
t
Положение переключателей
Uкод в делителе
 |  |
0 1 1 0 0 0 1 1
t
Рис.8.13.Графики, поясняющие работу кодоимпульсного вольтметра
Дата добавления: 2016-04-06; просмотров: 1140;