Законы пропорциональности. Подачи, напоры и мощности подобных машин.

При исследовании двух геометрически подобных насосов исходят из того, что режимы подобны, т.е. выдерживается кинематическое и динамическое подобие. Сизменением числа оборотов колеса насоса изменяются его производительность и напор. Если при различных числах оборотов режимы работы насоса подобны, то будут геометрически подобны и треугольники скоростей в любых сходственных точках потоков, в том числе на выходе из колеса (рис.3.1).

Рис. 3.1. Подобие треугольников скоростей.

Т.к. из уравнения Эйлера для работы центробежных насосов подача равна 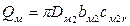, , то отношение подач натурного и модельного насоса составит:

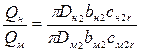(3.1)

В соответствии с первым и вторым условием гидродинамического подобия:

и поскольку , то

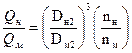(3.2)

Из уравнения (3.2) следует, что изменение производительности насоса пропорционально числу оборотов.

Формулы перерасчета напоров также вытекают из уравнения Эйлера, и отношение напоров модельного и натурного нагнетателей в конечном итоге имеет вид:

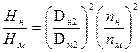(3.3)

Потребляемая насосом мощность пропорциональна произведению производительности Q на напор H. Учитывая зависимости (3.2) и (3.3), получим:

(3.4)

Согласно этому соотношению, изменение потребляемой мощности пропорционально кубам чисел оборотов.

Зависимости (3.2) — (3.4) носят название законов пропорциональности. Практически они достаточно точны при изменении чисел оборотов не более чем в два раза по сравнению с нормальными.

Формулы перерасчета Q, H, N, полученные на основе теории подобия, позволяют пересчитывать параметры, определяющие работу нагнетателей при изменении частоты вращения привода, диаметра рабочего колеса и плотности перемещаемой среды, а также характеристики натурных нагнетателей, полученные на модельных установках.