Кавитация. Кавитационный режим

В насосах при достижении определенных условий может возникнуть явление, называемое кавитацией. Под кавитацией понимают образование при снижении гидростатического давления пузырьков газа в толще движущейся жидкости и схлопывание этих пузырьков внутри жидкости в зоне, где гидростатическое давление повышается. В лопастном насосе кавитация возникает на лопатке рабочего колеса вблизи ее входной кромки, т. е. там, где скорость потока максимальна. В месте схлопывания пузырька (т.е. в момент его полной конденсации) возникает резкое увеличение давления (до сотен атмосфер). Если в этот момент пузырек пара находился на поверхности рабочего колеса или лопатки, то удар приходится на эту поверхность, что вызывает эрозию материала. Поверхность металла носит выщербленный характер. Процесс разрушения рабочих органов лопастных насосов является наиболее опасным следствием кавитации. Кавитация в лопастных насосах сопровождается резким шумом, треском и даже вибрацией насосной установки и, что особенно важно, падением напора, мощности, подачи и КПД.

Материалов, имеющих абсолютную устойчивость против кавитационного разрушения, не существует, поэтому работа насосов в кавитационном режиме не допустима. Это означает, что работа любого лопастного насоса должна осуществляться в бескавитационном режиме. Рассмотрим физическую картину возникновения кавитации в лопастном насосе при обтекании потоком лопасти рабочего колеса. Допустим, поток подходит к лопасти так, что в точке а линия тока раздваивается.

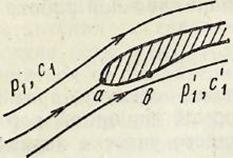
3.3. Схема обтекания потоком лопатки рабочего колеса.

Положение точки а для одного и того же насоса зависит от его подачи. Скорость относительного движения жидкости в точке в на тыльной стороне лопасти максимальна, поэтому давление в этой точке минимально. Предположим, что u₁ и p₁ - относительная скорость и давление в потоке перед входом на лопасть, а u^’₁, p^’₁ - относительная скорость и давление в точке в линии тока вдоль поверхности тыльной части лопасти, ρ — плотность жидкости. Запишем уравнение Д. Бернулли для относительного движения жидкости вдоль струйки, движущейся от точки а к точке в:

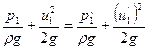(3.7)

В силу того, что точки а и в находятся на достаточно близком расстоянии друг от друга, потерями напора на этом участке можно пренебречь, а переносные скорости вращения этих точек можно считать равными.

Если понижать давление р₁ в потоке перед входом в рабочее колесо, оставляя неизменной подачу, то вследствие безотрывного течения жидкости скорости u₁ и u^’₁ не изменяются, а давление р^’₁ в точке в будет понижаться на ту же величину, что и давление р₁.

Как только по мере снижения давления р₁ давление в точке достигнет значения давления насыщенных паров р_t, то дальнейшее уменьшение давления в потоке жидкости на входе в колесо не будет сказываться на величине Р^’₁=Р_t. Как видно из уравнения Д. Бернулли (3.7), скорость относительного движения потока в точке в, равная:

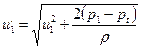(3.8)

Расход потока в межлопастном пространстве остается постоянным, вследствие чего струйки жидкости, движущиеся вблизи струйки аb, начнут двигаться с большей относительной скоростью, следовательно, с меньшим давлением в них. Таким образом, зона движения жидкости, в которой появляются пузырьки газов, постепенно расширяется с уменьшением давления перед входом потока в рабочее колесо. В тот момент, когда произойдет полный отрыв потока от тыльной стороны лопасти, резко уменьшится напор насоса.

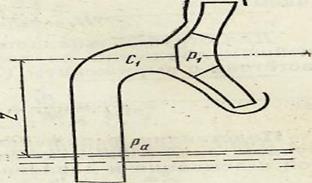
Как видно из приведенных достаточно простых описаний этого сложного явления, параметры насоса (напор и КПД) начинают меняться при достаточно развившейся кавитации. Основным средством, предупреждающим появление кавитации, является создание такого давления во всасывающем трубопроводе, при котором кавитация отсутствует. Как правило, это давление определяется высотой всасывания жидкости при работе насоса. Для нахождения высоты всасывания обратимся к следующим рассуждениям. Пусть р₁ и с₁ — давление и скорость течения жидкости перед рабочим колесом насоса (рис. 3.4), р_а — атмосферное давление на свободной поверхности, Z— превышение оси насоса над свободной поверхностью резервуара, из которого откачивается жидкость.

3.4. К определению давления в потоке на входе в рабочее колесо насоса.

Если потери напора во всасывающем трубопроводе до входа в рабочее колесо равны h_W, то уравнение Бернулли, записанное для струйки жидкости, движущейся от свободной поверхности жидкости до входа в рабочее колесо, запишется в виде:

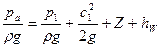(3.9)

Сумму 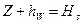называют статической высотой всасывания.

Тогда из выражения (3.3) для Н_s получаем:

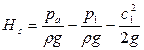(3.10)

Для струйки жидкости, попадающей при своем дальнейшем движении на лопатку рабочего колеса, в соответствии с выражением (3.7) имеем:

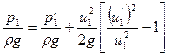(3.11)

Подставляя выражение (3.11) в формулу (3.9), получаем аналитическую связь между статической высотой всасывания и давлением р^’₁ в виде:

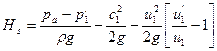(3.12)

Из выражения (3.10) видно, что снижением давления р₁ обусловливается увеличение статической высоты всасывания Н_s. Поскольку понижение давления р₁ вызывает уменьшение давления p₁^’ то, как это следует из выражения (3.12), наибольшего значения для данного насоса величина Н_s достигнет тогда, когда давление у тыльной части лопатки p₁^’ будет равно давлению насыщенных паров перекачиваемой жидкости, т. е. при .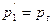

Дальнейшее увеличение статической высоты всасывания приведет к изменению характеристики насоса, поэтому достижение равенства 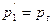определяет максимально допустимую статическую высоту всасывания. В этом случае выражение (3.12) можно записать в виде:

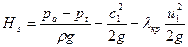(3.13)

где коэффициент 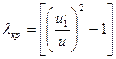для характерных кавитационных режимов называется критическим числом кавитации.

Назовем кавитационным запасом 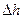превышение полного напора жидкости во всасывающем патрубке перед рабочим колесом над напором, создаваемым давлением насыщенных паров, т.е.

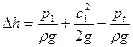(3.14)

Определим связь между кавитационным запасом и статической высотой всасывания, для чего в выражение (3.13) подставим значение р₁ из выражения (3.10) получим

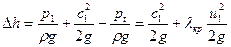(3.15)

Подставляя в выражение (3.13) полученное соотношение (3.15) получим:

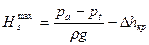(3.16)

Критический кавитационный запас Δh_кр соответствует критическому числу кавитации λ_кр..

Как видно из уравнения (3.16), чем больше кавитационный запас, тем меньше статическая высота всасывания и, следовательно, хуже кавитационные качества насоса.

Для определения критического кавитационного запаса проводят кавитационные испытания насоса. В результате для каждого режима работы насоса получают так называемую кавитационную характеристику, которая представляет собой зависимость напора и мощности насоса от кавитационного запаса при постоянной частоте вращения привода и подаче. Типичная кавитационная характеристика приведена на рис. 3.5.

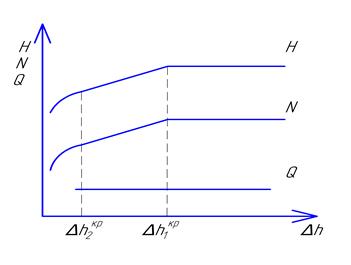
Рис. 3.5. Кавитационная характеристика центробежного насоса.

Как следует из приведенных выше рассуждений, при большом кавитационном запасе кавитации в потоке не наступает, напор и мощность от Δh не зависят. При достижении давления 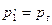начавшаяся кавитация приводит к уменьшению напора и мощности насоса. Режим, при котором начинается падение давления и мощности, называют первым критическим режимом. Ему соответствует первый критический кавитационный запас 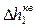, которому, в свою очередь, соответствует критическое число кавитации 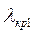.Это так называемая начальная стадия процесса кавитации, когда 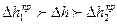и зона отрыва потока от лопатки невелика. Поэтому частично развившаяся кавитация мало сказывается на уменьшении напора и мощности насоса. Медленное уменьшение напора и мощности развивающейся кавитации заканчивается резким уменьшением последних, так как в результате развившейся кавитации происходит резкое увеличение концентрации парав потоке, что ведет к полному отрыву потока от лопатки рабочего колеса. Этому явлению соответствует второй критический кавитационный запас 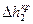, значение которого связано со значением второго критического числа кавитации .

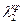У многих тихоходных насосов первый критический режим на кавитационной характеристике не обнаруживается. В этом случае приходится ограничиваться вторым критическим режимом. В качестве наименьшего кавитационного запаса принимают либо первый, либо второй критический кавитационный запас. Для предотвращения работы насоса в нежелательном кавитационном режиме обычно назначают небольшое превышение допустимого кавитационного запаса над критическим, т. е.

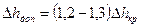(3.17)

Зная критический или допустимый кавитационный запас, можно найти для данной насосной установки допустимую, статическую высоту всасывания:

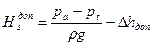(3.18)

Обычно принимают 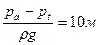, что соответствует наиболее часто встречаемому случаю всасывания холодной воды при нормальном давлении. В этом случае выражение (3.16) приобретает простой вид:

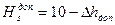(3.19)

Существенные трудности связаны с определением критического (или допустимого) кавитационного запаса, который в соответствии с уравнением (3.15) имеет вид:

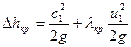(3.20)

Из этого уравнения следует, что критический кавитационный запас зависит только от скорости движения жидкости в рабочем колесе. Он мало зависит от вида и температуры жидкости. Таким образом, если потоки автомодельны, можно использовать теорию подобия для определения кавитационных характеристик подобных насосов. В результате С.С.Рудневым было предложено уравнение для определения критического кавитационного запаса, имеющее вид:

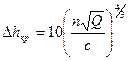(3.21)

где с — кавитационный коэффициент быстроходности.

Из выражения (3.21) следует, что кавитационные свойства насоса тем выше, чем больше величина с. При работе в оптимальном режиме плохих в кавитационном отношении насосов для первого критического режима можно принимать С=600-700, для нормальных насосов С=800-1000, для насосов с повышенными кавитаионными свойствами С= 1300-3000. Эти коэффициенты принимают безразмерными при подстановке в формулу (3.21) подачи Q, м³/с, п, об/мин, и Δh_кр, м.

Для насосов двухстороннего всасывания поток делится поровну между двумя входами в рабочее колесо. Для насосов двухстороннего входа в формулу (3.21) следует подставлять половинную подачу насоса, поэтому высота всасывания насоса двустороннего входа больше, чем одностороннего при прочих равных условиях.

Допустимая высота всасывания насоса при данном режиме работы может быть определена по формуле:

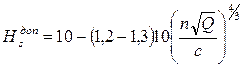(3.22)

Из анализа уравнения (3.20) следует, что улучшению кавитационных качеств насоса способствует увеличение входного диаметра и ширины рабочего колеса на входе. Наиболее эффективным является увеличение ширины рабочего колеса на входе, так как в этом случае не только улучшаются кавитационные качества насоса, но и не ухудшается его КПД.

Другим способом повышения кавитационных качеств насоса является установка на входе в рабочее колесо первой ступени осевого колеса, благодаря чему увеличивается давление на входе в колесо центробежного насоса.

Методы борьбы:

1. Применение колес с малой быстроходностью;

2. Ограничение числа оборотов рабочего колеса;

3. Охлаждение перекачиваемой жидкости;

4. Увеличение давления на всасе;

5. Ввод во всасывающий патрубок воздуха.