Вихревые линии и вихревые трубки

Потенциальное движение несжимаемой жидкости

Если 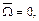то течение становится потенциальным (безвихревым). При этом будет выполняться условие

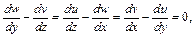(5.7)

что возможно при существовании функции 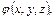удовлетворяющей условиям:

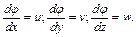(5.8)

Такое течение называется потенциальным. В этом случае циркуляция скорости на участке АВ определяется разностью потенциалов скоростей в точках А и В:

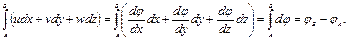(5.9)

Вихревые линии и вихревые трубки

Вихри скоростей образуют вихревое поле, в котором находятся вихревые линии и вихревые трубки. Из определения вихревой линии и вихревой трубки следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.

Вводя понятие потока вектора вихря скорости, равного

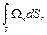(5.10)

где 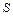- площадь поверхности; 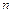- нормаль к поверхности, найдем, что поток вектора вихря скорости через вихревую поверхность будет равен нулю:

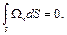(5.11)

Поток вектора вихря скорости сквозь произвольное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки (рис. 5.4):

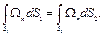(5.12)

Рис.5.4. Вихревая трубка

Это утверждение составляет вторую теорему Гельмгольца.

Поток вихря характеризует интенсивность вихревой трубки

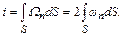(5.13)

При постоянной величине вихря 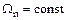получим

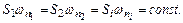(5.14)

откуда следует:

1) сечение вихревой трубки нигде не может стать равным нулю, т.к. бесконечно большая скорость вращения частиц физически невозможна;

2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца, либо «опираются» на стенку или на свободную поверхность.

Другой важной теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру один раз опоясывающему вихревую трубку, т.е.

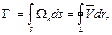(5.15)

где 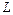- длина контура.