Подъемная сила, действующая на обтекаемое тело

На рыбообразном профиле (рис.5.7) в начале движения на верхней и нижней образующих скорости жидкости различны. Это приводит к образованию поверхности разрыва в области задней кромки профиля и к формированию кормового вихря.

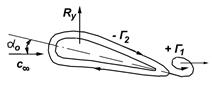
Рис.5.7. Образование подъемной силы рыбообразного профиля

Такой вихрь после отрыва от кромки обладает интенсивностью циркуляции 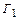. По теореме Томпсона на профиле возникает вихрь с циркуляцией 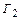противоположной по знаку циркуляции кормового вихря .

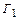Циркуляция скорости по теореме Н.Е.Жуковского вызывает подъемную силу на единицу длины профиля

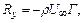(5.34)

где 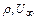- плотность и скорость набегающего потока.

Направление главного вектора сил давления определяется поворотом вектора скорости потока на 90° против направления циркуляции .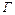

В пограничном слое на профиле суммарная интенсивность завихренности достигает больших значений.

В безвихревом плоскопараллельном потоке идеальной несжимаемой жидкости единственной силой, действующей на профиль, является подъемная сила. Отсутствие силы лобового сопротивления носит название парадокса Даламбера. Для практических расчетов используются коэффициенты подъемной силы 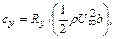где ширина (хорда) профиля, и сопротивления . Для случая плоской пластины . При малых углах атаки коэффициент подъемной силы пластины прямо пропорционален этому углу (рис.5.8).

Рис.5.8. Зависимость коэффициента подъемной силы профиля от угла атаки

Пример. Найти подъемную силу, действующую на бесконечно тонкую пластину длиной 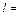0,5 м, при обтекании ее со скоростью 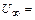30 м/с плоскопараллельным потоком газа плотностью 1,2 кг/м³, направленным под углом атаки 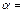16° (рис.5.9).

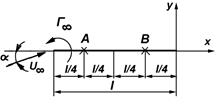
Рис.5.9. Система дискретных вихрей на плоской пластине

Решение. Для решения задачи используется метод дискретных вихрей. Схема расположения двух вихрей с циркуляциями и показана на рис.5.9. Значения циркуляции находятся из условия, что проекции скоростей на нормаль к поверхности пластины равны нулю. Тогда условие непротекания удовлетворяется в двух точках (А и В), а соответствующие уравнения имеют вид:

(5.35)

Преобразование этих уравнений с введением величины дает возможность решить систему

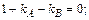
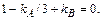(5.36)

Отсюда следует 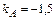; , поэтому подъемная сила примет значение

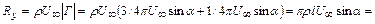
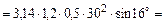467 Н/м. (5.37)