Для потенциального движения

Если во всей области движения жидкости

или (5.16)

где величины ротора скорости определяется с применением оператора набла ( ) в виде

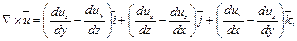= (5.17)

где 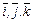- орты (единичные векторы) осей декартовой системы координат в направлениях X, Y, Z соответственно, то существует потенциал скорости и скорость имеет компоненты, определяемые по формуле

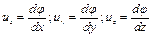(5.18)

или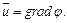

Уравнение Эйлера в форме Громеки - Ламба имеет вид

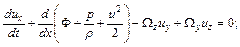
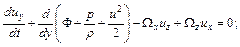
(5.19)

или в векторной форме

(5.20)

Условие потенциальности позволяет записать

(5.21)

Следовательно, выражение в скобках зависит только от времени, поэтому интеграл уравнения будет

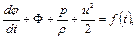(5.22)

где 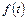- определяется из краевых условий. Этот интеграл уравнения Эйлера называется интегралом Коши - Лагранжа для потенциального движения идеальной несжимаемой жидкости.

Когда массовые силы сводятся силами тяжести, потенциал которых 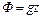, то интеграл Коши - Лагранжа принимает вид

(5.23)

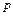В этом уравнении имеются два неизвестных и , поэтому следует использовать уравнение неразрывности

(5.24)

или

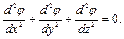(5.25)

Решение последнего уравнения Лапласа позволяет найти потенциал скорости , что с учетом равенства

(5.26)

определяет давление 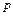. Произвольная функция 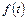будет найдена по величине в некоторой точке.

Для стационарного движения 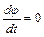и с учетом выражения потенциала массовой силы тяжести получим

Это интеграл Бернулли для потенциальной струйки идеальной несжимаемой жидкости.

Наиболее употребительна его форма вида

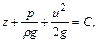(5.27)

где – геометрическая высота (удельная потенциальная энергия) положения сечения струйки; 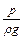- пьезометрический напор в сечении (удельная потенциальная энергия давления); - скоростной напор (удельная кинетическая энергия).