Вероятностные оценки ряда наблюдений.

При выполнении повторных измерений (наблюдений) одни и те же величины результата отдельных наблюдений отличаются друг от друга из-за наличия случайных погрешностей. Полным описанием случайной величины являются законы распределения вероятностей случайной величины. Закон распределения – соотношение устанавливающее связь между возможными значениями величины и соответствующими (или вероятностными).

Нормальный закон распределения (Гаусса). Он основан на двух аксиомах Гаусса: 1) при большом числе измерений погрешности одинаковые по величине и различные по знаку встречаются одинаково часто. 2) Малые погрешности встречаются чаще чем большие.

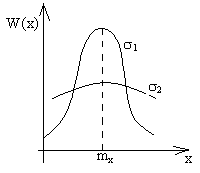
Закон распределения Гаусса через плотность распределения.

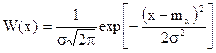s- средне квадратическое отклонение(СКО)

m_x-мат. ожидание.

s₁<s₂

Равномерный закон

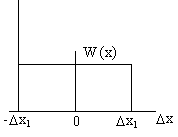Все значения равновероятны.

Основными характеристиками законов распределения являются математическое ожидание и дисперсия. Математическое ожидание ряда наблюдений – это величина относительно которой рассеиваются результаты отдельных наблюдений, если систематическая погрешность отсутствует, а разброс обусловлен только случайной погрешностью, то мат. ожиданием будет истинное значение измеряемой величины. Мат. ожидание непрерывной величины обозначается:

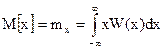
Бесконечные пределы соответственно требуют бесконечность измерений, что невозможно.

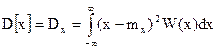Дисперсия – характеризует степень разброса (рассеивания) результатов наблюдения вокруг мат. ожидания. Чем меньше дисперсия, тем меньше разброс и тем точнее измерение. Дисперсия определяется как мат. ожидание квадрата центрированной величины.

Выражение в квадрате измеряемой величины (А², В², Ом²)

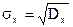Поэтому непосредственно её используют в качестве оценки точности. Поэтому в качестве хар-ки точности используют корень (+)