Обработка результатов измерений.

Необходимо из полученного ряда найти оценку мат. ожидания и дисперсии. Оценкой мат. ожидания является среднее арифметическое результатов отдельных наблюдений.

Отклонение между каждым из отдельных значений и средним арифметическим называется случайным отклонением или статичной погрешностью.

ρ=А_ср-a_i, Sρ_i=0

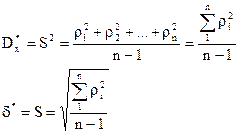*-оценка

А_ср®M[x] S²®D[x]

Действительное значение (А_ср) как результат обработки отдельных наблюдений, содержащих случайные погрешности, само по себе неизбежно содержит случайную погрешность. Степень близости действительного и истинного значений оценивается с помощью доверительного интервала. Доверительный интервал – интервал погрешностей, в котором погрешность измерений находится с заданной вероятностью.

В общем случае доверительный интервал может быть установлен, если известен закон распределения погрешности с основными его характеристиками.

Доверительный интервал выбирают при конкретных условиях измерения. Например: при нормальном законе часто используют ±36, Р_Д=0.9973. Это означает, что из 370 случайных погрешностей только одна погрешность будет больше 36, т. к. на практике число отдельных наблюдений 20-30.

Из теоремы вероятностей известно, что дисперсия среднего арифметического в n раз меньше дисперсии ряда наблюдений.

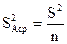, Для нахождения доверительного интервала необходимо найти закон распределения доверительной величины.

при известной дисперсии.

Теорема вероятностей доказывает, что для нормального закона распределения случайная погрешность Z есть случайная величина распределения по нормальному закону, at – случайная величина распределения по закону Стьюдента.

При n³30 закон Стьюдента совпадает с нормальным законом. Зная Z или t можно записать результат:

А_ист=А_ср±Zd_Аср или А_ист=А_ср±tS_Аср=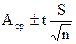

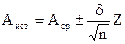
Лекция N6 22.03.02