Способы выражения и нормирования пределов погрешностей.

Погрешности устанавливаются в виде: абсолютной; относительной; приведённой; в виде числа деления шкалы.

Абсолютная погрешность – это разность между результатом измерения и истинным значением измеряемой величины.

D=X-X_и@X-X_{действительная}

Предел допустимой абсолютной погрешности выражается:

D=±a, где a-const;

D=±(a+bx) – линейная зависимость, где a и b const.

Нормирование по абсолютной погрешности имеет недостаток в том, что нельзя сравнивать по точности приборы различного назначения.

Относительная погрешность – это отношение абсолютной погрешности к значению измерительной величины

d=D/х*100% Имеет знак зависящий от знака абсолютной погрешности.

Предел относительной погрешности в процентах выражается:

А) d=±C, где С в процентах не мультипликативная погрешность.

Б) d=±[C+d(x_k/x-1)], где c и d постоянные числа (когда есть мультипликативная погрешность)

x_k – конечное значение диапазона измерения. В этой форме x_k и x берутся без учёта знаков.

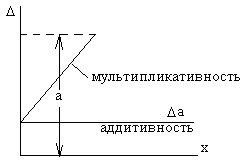
Недостатки относительной погрешности: при x®0 d®¥ и сравнения становятся бессмысленными.

Приведённые погрешности – отношение абсолютной погрешности к нормировочному значению

g=D/X_N*100%

Нормирующее значение – условно принятое значение, зависящее от вида шкалы прибора. Для СИ у которых нулевая метка находится на краю или вне шкалы нормирующее значение выбирается равным конечному значению диапазона измерений.

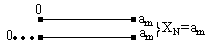
Дли СИ, у которых нулевая отметка находится внутри диапазона измерения – нормирующее значение равно арифметической сумме конечных значений диапазона.

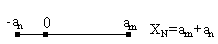
Для СИ предназначенных для измерения номинальных значений X_N равно этому номинальному значению .

Обобщённой метрологической хар-кой СИ является класс точности, который определяет допускаемые пределы всех погрешностей, а также все другие свойства влияющие на точность СИ.

Для СИ, пределы допускаемых погрешностей, которые выражаются в виде относительных или приведённых погрешностей, установлен ряд чисел для выражения пределов допускаемых погрешностей и применяемых для обозначения классов точностей.

(1, 1.5, 2, 2.5, 4, 5, 6)10ⁿ , где n=1, 0, -1, -2, -3, …

Для СИ у которых основную погрешность нормируют в виде предела приведённой погрешности, класс точности численно равен этому пределу.

Если предел допускаемой основной погрешности определяется по двучленной формуле, то в обозначении класса точности вводятся оба числа c и d через косую черту.

Пример задачи на экзамене.

Вольтметр, класс точности 0,5. С какой точностью измерено 100 вольт?

V=100,0±1,5 в 0.5=D/300*100

g=D/X_N*100% D=1,5 в

Правильность результата: погрешность не более 2-х значимых цифр. Последний разряд погрешности и последний разряд результата должны соответствовать друг другу.

Пример для цифрового вольтметра:

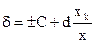
x_k=U_k=30в

x=U=100в

d=±[0,1+0,05*2]=0.2%