Философия Платона и математизация науки.

Платон (427-347 до н.э.) признается вершиной античной философии. Для нас он интересен тем, что ему принадлежит одна из оригинальных концепций науки. Влияние Сократа на Платона, как на своего ученика, очевидно и оно сконцентрировалось в учении о душе и познании. В построении же платоновской онтологии (метафизики) следует признать идейное влияние пифагорейцев и элеатов.

Началами всего являются Идеи-Эйдосы.Творчество Платона протекало в той традиции, где основой материальных явлений признавались нематериальные начала. Хотя пифагорейцы заполняли контур человека на земле счетными камешками и затем подсчитывали их количество для определения «числа человека», их числа не совпадали с камешками. Эту линию Платон усилил, назвав первоначала Идеями-Эйдосами. Они существуют не в головах людей, а вполне объективно и самостоятельно за пределами физического космоса. Идеи разительно отличаются от атомов и стихий Огня, Воздуха, Воды и Земли. Если последние вещественно-материальны, то Идеи родственны нематериальным числам, они идеальны. Идей много и они отличны друг от друга. Каждая Идея представляет высшее бытие и поскольку она отлична от других, эта «знаковость» выражает небытие всех остальных. Все Эйдесы организованны в иерархическую систему, на вершине которой пребывает «Благо-Единое». Оно придает значимость и бытие всем идеям и объединяет их в одно целое. Рангом ниже расположена Идея «Диада», с нее начинается многообразие и различие. Еще ниже пребывают: «Бытие», «Покой», «Движение», «Тождество», «Различие» и т.п.

Через геометрические фигуры Идеи формируют физический космос. Хотя Идеи самодостаточны, они выступают творческими образцами по отношению к материальному миру. Модель порождения представлена в диалоге «Тимей». По своему сценарию Платон ввел бога-демиурга. Он подобен вселенскому ремесленнику, который захотел создать прекрасный сосуд-космос, проявив при этом волю и разум. Источником последнего выступили Идеи, они стали исходными образцами творчества. Их активное влияние передалось на правильные геометрические тела, которые существуют рядом, но ценностью они «ниже» Эйдосов. Речь идет о четырех объемных многогранниках, имеющих упорядоченную геометрическую форму. Творческую силу Идей эти фигуры конкретизировали и породили стихии-элементы. Тетраэдр генерировал Огонь, октаэдр - Воздух, икосаэдр - Воду, куб - Землю.

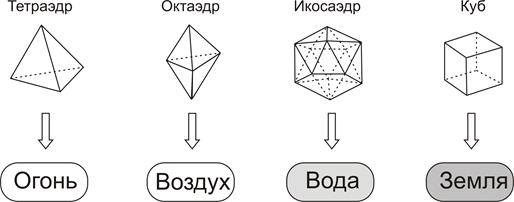
Данные посредники передали воздействие Идей на бесформенную и хаотическую «хору» или на «мать-кормилицу» (позднее Аристотель назовет это «материей). Она играет роль сырья, которое, подобно глине, принимает на себя влияние упорядочивающей силы и обретает форму. Структурирование материи завершается созданием физического космоса, где образуются все вещи и существа.

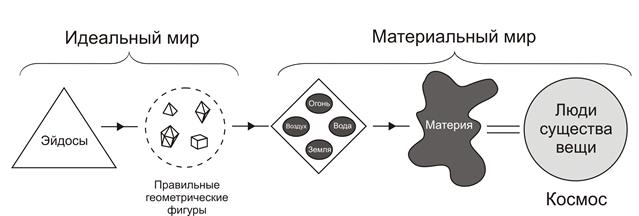
Только разумная душа способна познавать геометрические тела и Эйдосы. Еще до Платона возникло учение о человеке, соединяющем в себе тело и душу. Эту двойственность философ объяснил по-своему. Если тело обусловлено материальным миром, то душа причастна идеальному бытию. Человеческое тело демонстрирует чувственное познание, дающее образы вещей и субъективные мнения. Оно ограниченно материальностью. Высший тип познания принадлежит разумной душе. Ее родиной является идеальный мир и в душе запечатлены Идеи и правильные многогранники. Но когда душа попадает в тело, то конфликтная ситуация соединения блокирует мудрость и делает ее скрытной. Вот почему чувственное познание по-своему необходимо, оно должно запустить процесс «припоминания», который извлекает знания из глубины души.

Припоминание реализуется в виде рационального процесса. Исходный материал для него дает практический опыт, где чувства фиксируют наличие пестрого разнообразия вещей - маленьких и больших, круглых и квадратных, неравных и равных. Все эти очертания неопределенны и приблизительны, что и дает обычным людям текучие и изменчивые мнения. Но есть узкая группа лиц - математики и философы, способных на трудное дело размышления. Для них чувственные образы вещей и чертежей становятся предметом логических раздумий. В ходе них они приходят к понятиям точного равенства совершенных геометрических форм и строгих теорем. Путем умозаключений мыслители открывают в себе глубинные истины, что и является подлинным припоминанием того, что душа созерцала в идеальном мире. У припоминания есть своя большая логика: сначала математика, затем философия. На фронтоне платоновской академии была надпись «Негеометр, да не войдет». По своей сути и значимости правильные многогранники «ниже» Идей, поэтому философский разум, припоминающий Идеи, выше математического рассудка.

Платон определил становление античной теоретической математики. Как известно, греки заимствовали египетскую геометрию, вавилонскую арифметику и алгебру. Эта математика имела практический вычислительный характер и сводилась к набору частных правил-рецептов. Заслуга Платона состояла в том, что он выдвинул программу теоретизации. Ее онтологической основой стало учение об Идеях и геометрических телах, гносеологическим основанием выступила концепция рационального припоминания. Все это стимулировало математиков переходить от эмпирических образов к теоретическим понятиям. Определяющая роль здесь переходила к логике. Понятия формировались путем логических определений, аксиомы вводились четкими формулировками. Ядром получения теорем стало дедуктивное доказательство. Данная стратегия и выражала суть теоретизации - создания идеальных объектов («точка», «прямая», «угол», «параллельная прямая» и т. п.).

Новая программа утверждалась в борьбе с традицией. Платону пришлось неоднократно критиковать своих учеников, в частности, Евдокса (406-355 до н. э) за попытки доказывать геометрические теоремы посредством линейки и циркуля. Эти механические орудия ориентируют на зрительную оценку, а надо использовать силу ума с его логическими инструментами. Платон с негодованием осудил попытки некоторых учеников применить математику к механическим задачам («искусственный голубь» и т.п.) Теоретическая математика должна остаться «чистой» наукой, далекой от материальных вещей.

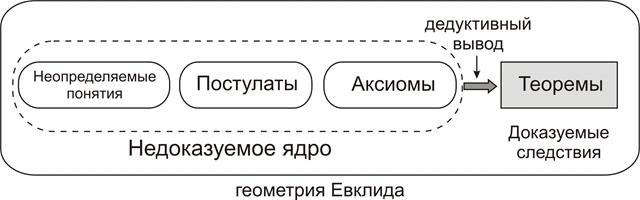
Геометрия Евклида – первая систематическая теория.Ярким образцом реализации платоновской программы стала геометрия Евклида (IV-III в. до н.э.). Живя в Александрии, основанной Александром Македонским, он написал классический труд по математике - «Начала». Здесь все выстроено по правилам теоретической логики. Сначала даны определения исходных понятий: «точка есть то, что не имеет частей»; «линия есть длина без ширины» и т. п. По сути дела это не определения, а вполне законные тавтологии. Затем введены пять постулатов, представляющие собой правила построения основных геометрических фигур: «через две точки можно провести только одну прямую»; «из любой точки как из центра можно провести окружность любого радиуса» и т.п. Все постулаты были простыми и очевидными утверждениями за исключением пятого, где параллельные прямые сопрягались с бесконечностью, что для античного ума представлялось сложным. Третью группу утверждений составили аксиомы как содержательные характеристики объективного пространства и реальности: «равные одному и тому же равны между собой», «целое больше части» и т. п. Количество аксиом относительно небольшое, они взаимонезависимы и не выводятся из других положений в силу своей самоочевидности. Исходя из исходных понятий, постулатов и аксиом, Евклид выводил теоремы и тем самым осуществлял их доказательство. Такой способ образования идеальных объектов получил название дедуктивно-аксиоматического метода и геометрия Евклида до сих пор остается образцом научной теории.

Проект математического спасения явлений неба.Единственной областью приложения новой математики Платон признал астрономию. Он полагал, что небо сродни идеальному миру, ибо его объекты выражают скрытый порядок геометрических тел. Доплатоновская астрономия сочетала в себе умозрительные идеи с результатами наблюдений. Космос признавался в виде огромной сферы, в центре которой находится планета Земля. Кроме чувственного опыта земных наблюдений здесь использовался натурфилософский довод – из всех элементов Земля является самым тяжелым и потому центральное место нашей планеты естественно. Самой дальней и конечной является сфера неподвижных звезд, между Землей и звездами движутся Солнце, Луна и планеты. Особенно хаотичное движение демонстрируют планеты, они останавливаются, двигаются вспять, что в итоге дает петли-восьмерки и потому планеты похожи на бродячих лошадей (греч. planetоs - бродяга). Кроме того, одни и те же планеты в разное время года давали разный блеск (сильный – слабый). Если вавилоняне и египтяне составляли из таких фактов регистрирующие таблицы и на этом успокаивались, то Платон выдвинул программу – за видимым беспорядком нужно искать скрытый математический порядок. Теория должна объяснить факты и тем самым «спасти явления» перед судом теоретического разума.

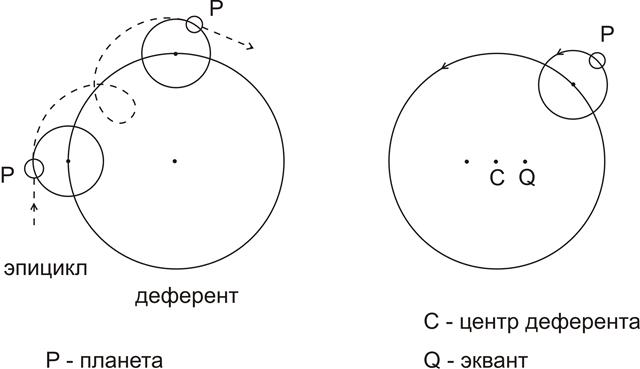
По этому пути и пошли ученики Платона. За основу они взяли из геометрии фигуры круга и сферы. Речь шла о самых совершенных и правильных пространственных формах. Часть «лошадиных путей» (восьмерок) распутал Евдокс, он вложил друг в друга 27 концентрических сфер. По три сферы пришлось на Солнце и Луну, по четыре сферы получила каждая из пяти планет. Углы наклона осей и равномерные скорости вращения сфер были подобраны так, что сложные движения объяснялись комбинацией движений нескольких сфер, и это позволяло осуществлять предсказания положения небесных тел в будущем. И все же Евдокс не смог объяснить движения Венеры и Марса, изменения яркости и видимых размеров планет. «Восьмерки» двух планет объяснил другой ученик Платона - Гераклид Понтийский (IV в. до н. э.). Он признал суточное вращение Земли, а Венера и Меркурий у него стали вращаться вокруг Солнца. Гераклид внес важное математическое новшество в виде схемы эпицикла (видимая петля здесь является продуктом того, что планета участвует в одновременном вращении большого и малого кругов. Центр последнего движется по другому кругу.)

Развитие платоновского проекта.Программа была принята после дующими поколениями астрономов. Она усиленно конкретизировалась и обрастала новациями. Важный вклад внес Гиппарх (190-125 до н. э.). Он осознал, что схема Евдокса противоречит многим наблюдательным фактам и надо развивать идею эпицикла. Сочетая эпициклы и эксцентрические движения, надлежащим образом подбирая радиусы и скорости окружностей, Гиппарх сумел довольно точно описать движения всех крупных небесных тел. лунное затмение он предсказывал с точностью до одного-двух часов.

Вершиной античной астрономии стала теория Клавдия Птолемея (100-168). Как представитель александрийской школы он занимался географией, оптикой, астрологией и все же его основным направлением была астрономия. В первой части главного труда «Математическое построение» («Альмагест») изложена тригонометрия, необходимая для астрономических вычислений. Затем обсуждается вопрос о центре мироздания. Птолемей знал о гелиоцентрической догадке Аристарха Самосского (III в. до н. э.) и отверг ее под влиянием физических доводов. Скорость движения любого тела пропорциональна его весу. Если бы Земля двигалась, то она оставила бы далеко позади себя более легкие тела: облака, птиц, животных и людей. Поскольку такое не происходит, Земля является неподвижным центром, вокруг которого движутся Луна, Солнце и планеты.

В девятой части книги сформулирована задача – надо доказать, что все видимые нерегулярности Солнца, Луны и пяти планет объяснимы по средством равномерных круговых движений. Такую цель и поставил Платон. Для ее достижения Птолемей использовал все достижения своих предшественников: деферент, эксцентрик и эпицикл. Комплексную схему он смог дополнить собственным открытием – эквантом, позволившим еще лучше увязать круговые движения с наблюдательными фактами. Теория Птолемея стала основой астрономии до середины XVI в.

Перспективы и ограничения.Платон существенно углубил и развил пифагорейскую догадку о математике как основе познания. В его философии она предстала в рациональной форме, доступной для широкого круга ученых. И все же на платонизме лежал отпечаток ограниченности, присущий всему эллинскому мировоззрению. Речь идет об универсальной геометризации, где все сводится к пространственной фигуре (многогранники). Геометрия здесь подавляет арифметику и алгебру. Последующее развитие науки устранило этот перекос. Но даже при таком дисбалансе программа Платона сохранила высокую значимость у современных ученых. В. фон Гейзенберг (1901-1975) как один из основателей квантовой физики признался, что в поиске скрытых математических симметрий микромира он вдохновлялся идеями Платона.